0.999
数学、0.999 …(とも書かれた0。9に、小数点表記を繰り返す)である循環小数後9Sの果てしない配列からなる小数点を。この循環小数は、シーケンス内のすべての10進数(0.9、0.99、0.999、…)以上の最小数を表します。この数は1です。つまり、「0.999 …」は「ほぼ正確」または「非常に、非常に近いが、完全ではない」1ではなく、「0.999 …」および「1」です。まったく同じ番号を表します。
循環小数は無限に続きます
直感的な議論から数学的に厳密な 証明まで、この平等を示す方法はたくさん使用される手法は、対象読者、背景の仮定、歴史的背景、および実数の好ましい開発、つまり0.999 …が一般的に定義されているシステムによって異なります。他のシステムでは、0.999 …は同じ意味、異なる定義、または未定義である可能性が
より一般的には、すべての非ゼロ終端小数点以下はすべての特性である二つの等しい表現(例えば、8.32および8.31999 …)を有する位置においてシステムに関係なく表現ベース。終了する小数表現に対する功利主義的な好みは、それが唯一の表現であるという誤解の一因となっています。これと他の理由(非基本的な技術、特性、または規律に依存する厳密な証明など)のために、一部の人々は、平等が十分に直感に反しているため、疑問を呈したり拒否したりすることがこれは、数学教育におけるいくつかの研究の主題となっています。
コンテンツ
1 初等的証明
1.1 直感的な説明 1.2 完全性に関する議論 1.3 厳密な証明
2 代数的議論
3 分析的証明
3.1 無限のシリーズとシーケンス 3.2 ネストされた間隔と最小の上限
4 実数の構成からの証明
4.1 デデキント切断 4.2 コーシー列 4.3 無限小数表現 4.4 密な注文
5 一般化
5.1 独自の表現の不可能性
6 アプリケーション
7 教育における懐疑論
8 文化現象
9 代替番号システムでは
9.1 無限小 9.2 ハッケンブッシュ 9.3 減算の再検討 9.4 p進数 9.5 超有限性
10 関連する質問
11 も参照してください
12 ノート
13 参考文献
14 参考文献
15 外部リンク
初等的証明

アルキメデスの性質:任意のポイント
のx点の2間のフィニッシュラインの嘘の前にNS
{ P_ {n}}
(包括的)。
方程式0.999 … = 1の初等的証明がこれは、シリーズ、極限、実数の正式な構築などのより高度なトピックを参照せずに、(有限の)10進数の比較と加算の数学ツールのみを使用します。証明、Stillwell(1994、p。42)によって与えられた演習は、数字の線に0.9、0.99、0.999などを引くと、余地がないという直感的な事実を直接形式化したものです。それらと1の間に数字を置きます。0.999…という表記の意味は、0.9、0.99、0.999などのすべての数字の右側にある数字の線上の最小点です。最終的には1の間にスペースがないためです。これらの数値では、ポイント1はこの最小のポイントである必要があるため、0.999 … = 1です。
直感的な説明
数直線上に0.9、0.99、0.999などを配置すると、これらの点はすべて1の左側にあり、1に近づくことがすぐにわかります。
より正確には、0.9から1までの距離がある= 1/10 0.1、150から1までの距離は、0.01 = 1/10 2、など。n番目のポイント(小数点以下n 9sのポイント)から1までの距離は1 / 10nです。
したがって、1が0.9、0.99、0.999などを超える最小の数値でない場合、1とこれらすべてのポイントの間にある数直線上のポイントが存在します。この点未満である1からの正の距離であろう1/10 nはすべてのための整数 N。標準的に数システム(有理数と実数)未満でない正の数が存在しない1/10 nはすべてのためのNが。これはアルキメデスの性質(の1つのバージョン)であり、有理数のシステムで保持されることが証明できます。したがって、1が最小のすべて0.9、0.99、0.999、等よりも大きい数であり、そうである= 0.999 1 …。
完全性に関する議論
何この引数ショーの一部が存在することである上限以上のシーケンス0.9、0.99、0.999、等:シーケンスのすべての条項よりも大きい最小の数の。実数システムの公理の1つは、完全性公理です。これは、すべての有界シーケンスの上限が最小であることを示しています。この最小上限は、無限小数展開を定義する1つの方法です。無限小数で表される実数は、その有限切り捨ての最小上限です。ここでの引数は、完全性が有効であると仮定する必要はありません。これは、この特定の有理数のシーケンスが実際に最小の上限を持ち、この最小の上限が1に等しいことを示しているためです。
厳密な証明
数直線上の点としての数とその表現との関係を適切に定義することができないため、前の説明は証明ではありません。証明の正確さのために、小数点の後にn個の9がある数値0.999 … 9は、0。(9)nで表されます。したがって、0。(9)1 = 0.9、0。(9)2 = 0.99、0。(9)3 = 0.999などになります。1/10 N = 0.0 … 01と、nは小数点の後の桁、小数点数の加算規則は、意味します 0。 (( 9
)。+1 / 0=
1 { 0.(9)_ {n} + 1/10 ^ {n} = 1、}
と 0。(( 9
)。<
1 { 0.(9)_ {n} <1、}
すべての正の整数 nに対して。
1がすべて0以上の最小数であることを示さなければなりません。(9)n。このためには、数xが1より大きくなく、すべて0.(9)n以上の場合、x = 1であることを証明するだけで十分です。したがって、xを次のようにします 0。 (( 9
)。≤ ≤
1 { 0.(9)_ {n} leq x leq 1、}
すべての正の整数 nに対して。したがって、
1− 1 ≤ 1
− ≤1 − 0。(( 9
)。。
{ 1-1 leq 1-x leq 1-0。(9)_ {n}。}
これは、基本的な算術と上記で確立された最初の等式を使用して、0 ≤ 1
− ≤1 / 0。
{ 0 leq 1-x leq 1/10 ^ {n}。}
これは、1とxの差が、正の整数の逆数よりも小さいことを意味します。したがって、この差はゼロでなければならず、したがってx = 1です。あれは.999 … =
1.1。
{ 0.999 ldots = 1。}
この証明は、ゼロが整数のすべての逆数よりも小さい唯一の非負の数であるという事実、または同等に、すべての整数よりも大きい数がないという事実に依存しています。これはアルキメデスの性質であり、有理数と実数について検証されます。実数は、無限に小さい数(無限大)と無限に大きい数(無限数)を持つ超実数などの数体系に拡大できます。このようなシステムを使用する場合、すべて0.(9)n以上の最小数がないため、表記0.999 …は通常使用されません。(これは事実によって暗示された0(9)N ≤ X <1意味0(9)N -1 ≤2 X - 1 < X <1 )。
代数的議論
平等の過度に単純化された図解の問題は、教育学的議論と批評の主題です。バイヤーズ(2007年、P。39)は、小学校では、1がいることを教えているという議論議論1 / 3 = 0.333が…、そう、すべての重要な機微を無視して、「乗算」することによって、このアイデンティティー3が与え= 0.999 1を… 。。彼はさらに、等号の意味に関する未解決のあいまいさのために、この議論は説得力がないと言います。学生は、「1という数字が0.999という表記で意味されているものと同じであるという意味ではありません。…」と考えるかもしれません。バイヤーズが遭遇したほとんどの学部数学専攻は、0.999 …がこの議論の強さで1に「非常に近い」と感じていますが、「無限に近い」とさえ言っている人もいますが、等しいと言う準備はできていません1.にリッチマン(1999)「この引数は、ほとんどの人が思考することなく、第1の式を受け入れるように教え込まれてきたという事実から、その力を得る」方法を説明するだけでなく、引数がこの仮定に疑問を懐疑論者を引き起こすことを示唆しています。
Byersはまた、次の議論を提示します。させて =0.999 …
10 =9.999 …
を「掛ける」ことによって 10 10 =9 + 0.999 …
整数部分を「分割」することによって
10 = 9 + の定義による 9 = 9 引くことによって NS= 1
で割ることによって 9 { { begin {aligned} x&= 0.999 ldots \ 10x&= 9.999 ldots && { text {by “”multiplying”” by}} 10 \ 10x&= 9 + 0.999 ldots && { text {by “”整数部分を分割する」}} \ 10x&= 9 + x && { text {の定義による}} x \ 9x&= 9 && { text {減算による}} x \ x&= 1 && { text {による除算}} 9 end {aligned}}}
最初の引数を受け入れなかった学生は、2番目の引数を受け入れることがありますが、バイヤーズの意見では、あいまいさをまだ解決していないため、無限小数の表現を理解しPeressini&Peressini(2007)は、同じ議論を示しており、平等を説明していないと述べており、そのような説明には無限大と完全性の概念が含まれる可能性が高いことを示しています。Baldwin&Norton(2012)は、Katz&Katz(2010a)を引用して、これらのような議論に基づくアイデンティティの扱いは、正式な制限の概念がなく、時期尚早であると結論付けています。
同じ議論がRichman(1999)によっても与えられており、懐疑論者はxがキャンセル可能かどうか 、つまり、両側からxを引くことが理にかなっているかどうかを疑問視する可能性があると述べています。
分析的証明
0.999 …の質問は数学の正式な開発に影響を与えないため、実際の分析の標準的な定理が証明されるまで延期することができます。1つの要件は、オプションの符号、整数部分を形成する1つ以上の数字の有限シーケンス、小数点、および小数部分を形成する数字のシーケンスで構成される、10進表記で記述できる実数を特徴付けることです。0.999 …について説明するために、整数部分はb 0として要約でき、負の値は無視できるため、10進数の展開は次の形式になります。 0
。 1 2 3 4 5
… { b_ {0} .b_ {1} b_ {2} b_ {3} b_ {4} b_ {5} dots。}
小数部分は、整数部分とは異なり、有限の桁数に制限されません。これは位取り記数法であるため、たとえば、500の5の数字は50の5の10倍になり、0.05の5は0.5の5の10分の1になります。
無限のシリーズとシーケンス
10進表現
10進展開の一般的な開発は、それらを無限級数の合計として定義することです。一般に: 0
。 1 2 3 4 … = 0 + 1 (( 1 10 )。 + 2 (( 1 10 )。2 3(( 1 10 )。3 4(( 1 10 )。4
⋯ { b_ {0} .b_ {1} b_ {2} b_ {3} b_ {4} ldots = b_ {0} + b_ {1} left({ tfrac {1} {10}} right)+ b_ {2} left({ tfrac {1} {10}} right)^ {2} + b_ {3} left({ tfrac {1} {10}} right)^ { 3} + b_ {4} left({ tfrac {1} {10}} right)^ {4} + cdots。}
0.999の場合…等比数列に関する収束定理を適用できます:
もしも
| |< 1
{ | r | <1}
それから
NS + NS 2 + NS3 ⋯ = NS 1 − 。
{ ar + ar ^ {2} + ar ^ {3} + cdots = { frac {ar} {1-r}}。}
0.999ので…このようなAの和である= 9と共通比R =
1 / 10、定理は、質問の短い作業を行います。.999 … = 9(( 1 10 )。+ 9(( 1 10 )。2 9(( 1 10 )。3 ⋯ = 9(( 1 10 )。 1 −1 10 = 1.1。
{ 0.999 ldots = 9 left({ tfrac {1} {10}} right)+9 left({ tfrac {1} {10}} right)^ {2} + 9 left ({ tfrac {1} {10}} right)^ {3} + cdots = { frac {9 left({ tfrac {1} {10}} right)} {1-{ tfrac {1} {10}}}} = 1。}
この証明は、早くも1770年にレオンハルトオイラーの代数の要素に現れます。

制限:1に収束する4進法の分数シーケンス(.3、.33、.333、…)を含む単位間隔 等比数列の合計自体は、オイラーよりも古い結果です。典型的な18世紀の派生では、上記の代数証明と同様の用語ごとの操作が使用され、1811年までに、ボニーキャッスルの教科書「代数の紹介」では、等比数列のこのような議論を使用して、0.999での同じ操作を正当化しています。 。そのようなリベラルな合計方法に対する19世紀の反応は、今日でも支配的な定義をもたらしました。級数の合計は、その部分的な合計のシーケンスの限界として定義されます。対応する定理の証明は、そのシーケンスを明示的に計算します。それは、微積分または分析の証明ベースの紹介で見つけることができます。
配列(X 0、xは1、xは2 ···)が限界 Xを距離場合| x − x n | nが大きくなると任意に小さくなります。0.999 … = 1というステートメント自体は、制限として解釈および証明できます。.999 …= e リム
∞0。 9 … 9
⏟ = e リム
∞∑ k=19 10 = リム ∞ (( 1− 1
10 )。= 1 −
リム 1
10 =1 − 0 =
1.1。
{ 0.999 ldots { overset { underset { mathrm {def}} {}} {=}} lim _ {n to infty} 0. underbrace {99 ldots 9} _ { n} { overset { underset { mathrm {def}} {}} {=}} lim _ {n to infty} sum _ {k = 1} ^ {n} { frac { 9} {10 ^ {k}}} = lim _ {n to infty} left(1-{ frac {1} {10 ^ {n}}} right)= 1- lim _ {n to infty} { frac {1} {10 ^ {n}}} = 1 、-、0 = 1。}
最初の2つの等式は、シンボルの省略定義として解釈できます。残りの平等は証明することができます。最後のステップ、という
1 / 10のn 0としてのn ∞、しばしばによって正当化されるアルキメデスの性質実数の。0.999 …に対するこの制限ベースの態度は、多くの場合、より刺激的ですが、正確性の低い用語で表現されます。たとえば、1846年の教科書The University Arithmeticは、「。999 +、無限大= 1まで継続しました。これは、9を併合するたびに値が1に近づくためです」と説明しています。1895年の学校向け算数では、「9を多数取ると、1と.99999 …の差は考えられないほど小さくなります」と述べています。このようなヒューリスティックは、0.999 …自体が1未満であることを意味するものとして学生によって誤って解釈されることがよく
ネストされた間隔と最小の上限
ネストされた間隔
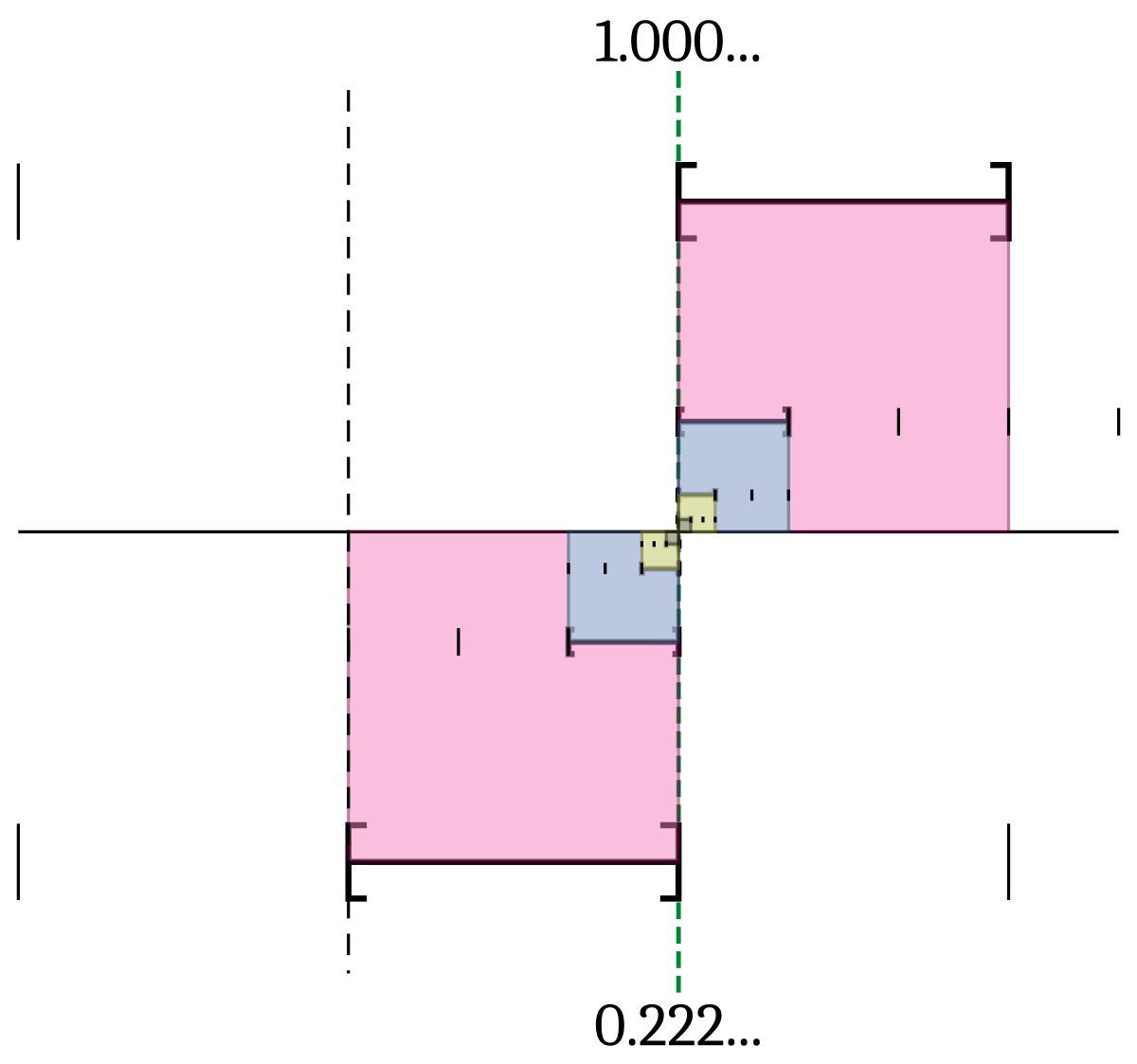
ネストされた区間:基数3で、1 = 1.000 … = 0.222 .. ..
上記の級数の定義は、小数展開で指定された実数を定義する簡単な方法です。補完的なアプローチは、反対のプロセスに合わせて調整されます。特定の実数に対して、小数展開を定義して名前を付けます。
実数xが閉区間にあることがわかっている場合(つまり、0以上10以下)、その区間を10個に分割して重なり合うだけにすることを想像できます。エンドポイント:、、など、まで。番号xはこれらのいずれかに属している必要がに属する場合は、数字「2」を記録し、その間隔を、、…、、に分割します。このプロセスを続行すると、ネストされた間隔の無限のシーケンスが生成され、数字の無限のシーケンスb 0、b 1、b 2、b 3、…でラベル付けされ、1回の書き込みが行われます。 = 0
。 1 2 3 … { x = b_ {0} .b_ {1} b_ {2} b_ {3} ldots}
この形式では、恒等式1 = 0.999 …と1 = 1.000 …は、それぞれ、1がとの両方にあるという事実を反映しているため、検索時にどちらかのサブインターバルを選択できます。その数字。この表記が「=」記号を乱用しないようにするには、小数ごとに一意の実数を再構築する方法が必要です。これは制限付きで行うことができますが、他の構造は順序付けのテーマを継続します。
簡単な選択の1つは、入れ子になった区間の定理です。これは、長さが任意に小さくなる入れ子になった閉じた区間のシーケンスが与えられた場合、区間の交点に実数が1つだけ含まれることを保証します。だから、B 0。B 1 、B 2 、B 3 …一意の番号であると定義される[すべての間隔内に含まれるbは0、B 0 + 1]、[ B 0。B 1、B 0。b 1 +0.1]など。0.999 …は、のすべての有限文字列の、、、および[0.99 … 9、1]のすべての区間にある一意の実数です。 9秒。1はこれらの各区間の要素であるため、0.999 … = 1です。
有無:ネストされた間隔定理は通常、実数のより基本的な特性に設立された少なくとも上限またはSUPREMA。これらのオブジェクトを直接利用するためには、定義することができるB 0。B 1 、B 2 、B 3 …上部approximants {一連の結合以上であると、B 0、B 0。B 1、B 0。b 1 b 2、…}。次に、この定義(またはネストされた区間の定義)が細分化手順と一致していることを示すことができます。これは、0.999 … = 1を意味します。トム・アポストルは次のように結論づけています。
実数が2つの異なる小数表現を持つ可能性があるという事実は、2つの異なる実数のセットが同じ上限を持つことができるという事実を単に反映したものです。
実数の構成からの証明
実数の構成
一部のアプローチでは、公理的集合論を使用して、実数を有理数に基づいて構築された特定の構造として明示的に定義します。自然数 – 0、1、2、3、というように-すべての数が後継者を持っているのでこと、0で始まり、上向きに続けます。自然数をその負数で拡張してすべての整数を与え、さらに比率に拡張して有理数を与えることができます。これらの数体系には、足し算、引き算、掛け算、割り算の算術が伴います。より微妙に、それらには順序付けが含まれているため、ある数値を別の数値と比較して、別の数値よりも小さい、大きい、または等しいことがわかります。
有理数から実数へのステップは、主要な拡張です。このステップを達成するための一般的な方法は少なくとも2つあり、どちらも1872年に公開されています。デデキント切断とコーシー列です。これらの構造を直接使用する0.999 … = 1の証明は、過去数十年間の現代の傾向が公理分析を使用することであった実際の分析に関する教科書には見られません。構造が提供される場合でも、それは通常、実数の公理を証明するために適用され、それが上記の証明をサポートします。ただし、何人かの著者は、構造から始めることがより論理的に適切であり、結果として得られる証明はより自己完結型であるという考えを表明しています。
デデキント切断
デデキント切断
でデデキント切断アプローチ、各実数xがとして定義される無限集合全ての有理数x未満。特に、実数1は、1未満のすべての有理数の集合です。正の小数展開はすべて、デデキント切断を簡単に決定します。つまり、展開のある段階よりも小さい有理数の集合です。 。実数0.999よう…有理数の集合であるrのようにR <0、又はR <0.9、またはR <150、またはrは、フォームのいくつかの他の数未満である
1− 1
10 = 0。 (( 9
)。=0。 9 … 9
⏟ ナイン { 1-{ frac {1} {10 ^ {n}}} = 0.(9)_ {n} = 0。 underbrace {99 ldots 9} _ {n { text {nines}} }。}
0.999 …のすべての要素は1未満であるため、実数1の要素です。逆に、1のすべての要素は、次のように記述できる有理数です。 NS < 1 { { frac {a} {b}} <1、}
B > 0とB >。これは、 1 − NS= − NS ≥ 1>> 1 10 、
{ 1-{ frac {a} {b}} = { frac {ba} {b}} geq { frac {1} {b}}> { frac {1} {10 ^ {b }}}、}
{frac {1}{10^{b}}},}””>
したがって NS 1− 1
10 。
{ { frac {a} {b}} <1-{ frac {1} {10 ^ {b}}}。}
それ以来1 − 1
10 = 0。 (( 9
)。<0.999 …
{ 1-{ frac {1} {10 ^ {b}}} =0。(9)_ {b} <0.999 ldots}
上記の定義により、1のすべての要素は0.999 …の要素でもあり、0.999 …のすべての要素も1の要素であるという上記の証明と組み合わせると、0.999 …と1のセットには0.999 …が含まれます。同じ有理数、したがって同じセット、つまり0.999 … = 1です。
デデキント切断としての実数の定義は、1872年にリヒャルト・デーデキンドによって最初に公開されました。各小数展開に実数を割り当てる上記のアプローチは、「Is 0.999 … = 1?」というタイトルの解説論文によるものです。でフレッド・リッチマンにより数学誌、 、特にジュニア/シニアレベル、および学生で、大学の数学の教師を対象としています。リッチマンは、有理数の密なサブセットでデデキント切断を行うと同じ結果が得られると述べています。特に、彼は小数を使用します。これは、証明がより迅速に行われるためです。彼はまた、通常、定義では{x:x <1}をカットすることはできますが、{x:x≤1}(またはその逆)は許可しないと述べています。 1. したがって、実数の従来の定義では、方程式0.9 * = 1が最初に組み込まれていることがわかります。」手順をさらに変更すると、2つが等しくない別の構造になります。それは一貫しているが、小数点算術もはやホールドの共通のルールの多くは、例えば、分数
1 / 3が全く表現を持っ以下の「代替番号システム」を参照して
コーシー列
コーシー列
別のアプローチは、実数を有理数のコーシー列の極限として定義することです。この実数の構成では、有理数の順序をあまり直接的に使用しません。まず、xとyの間の距離を絶対値|として定義します。x − y |、ここで絶対値| z | はzと− zの最大値として定義されるため、負になることはありません。次に、実数は、この距離を使用してコーシー列プロパティを持つ有理数の列として定義されます。すなわち、(配列では、X 0、xは1、xは2、任意の正の有理数のための有理数への自然数からマッピング、…)δは存在するN |よう x m − x n | ≤ δすべてのためのM、N > N。(項間の距離は、正の有理数よりも小さくなります。)(場合X N)および(Y nは)は、2つのコーシー配列であり、それらは、配列(あれば実数として等しくなるように定義されるX N – Y nが上限進数の0トランケーション有する)B 0。b 1 b 2 b 3 …コーシー列である有理数のシーケンスを生成します。これは、数値の実際の値を定義するために使用されます。したがって、この形式では、タスクは有理数のシーケンスが(( 1− 1 − 9 10 1 − 99
100 …
)。 = (( 1 1 10 1 100 … )。 { left(1-0,1- {9 over 10}、1- {99 over 100}、 dots right)= left(1、{1 over 10}、{1 over 100}、 dots right)}
考慮限界0有するn個のシーケンスの第用語を、nは∈ { mathbb {N}}
、したがって、次のことを示す必要があります
リム 1
10 = 0。 { lim _ {n rightarrow infty} { frac {1} {10 ^ {n}}} = 0。}
制限の定義を理解していれば、この制限は明白です。したがって、再び0.999 … = 1です。
実数の定義コーシー列が最初で個別に出版されたとしてエドゥアルト・ハイネとゲオルク・カントールも1872年には、 0.999 … = 1は、密接グリフィス&ヒルトンの1970年に従うことを証明含め小数展開は、上述のアプローチ作品古典的な数学の包括的な教科書:現代的な解釈。この本は、現代的な観点からおなじみの概念を再検討するために特別に書かれています。
無限小数表現
実数の構成§Stevinの構成
一般に、中等学校の数学教育では、実数は、整数の後に基数点が続き、任意の実数の小数部分を表す文字列として書き出される無限のシーケンスを使用して数を定義することによって構築されます。この構成では、小数点(または基数10以外のシステムでは基数)の後の整数と数字の任意の組み合わせのセットが実数のセットです。この構造は、1 = eq 0.999 …を定義するセットの同値関係を定義した後、および10進数の文字列にゼロ以外の項が有限個しかない他の非ゼロの10進数について、すべての実公理を満たすように厳密に示すことができます。末尾の9sバージョン。この実数の構成法では、「1 = 0.999 …」というステートメントのすべての証明は、実数に対して何らかの演算が実行されるときに、暗黙的に等式を仮定していると見なすことができます。
密な注文
密な注文
この問題を解決できる概念の1つは、実数が密に順序付けられているという要件です。学生はそれを当然のことと思っています
0.99999..。
{ 0.99999 …}
前です 1 { 1}
一方、この種の直感的な順序付けは、純粋な辞書式順序としてより適切に定義されます。
「…実数の順序は密な順序として認識されます。ただし、コンテキストに応じて、学生はこのプロパティを、指定された数の直前または直後の数の存在と調整できます(0.999 …がよく見られます) 1)の前身として。」
密な順序では、厳密に3番目の実際の値が存在する必要があります
0.99999..。
{ 0.99999 …}
と 1 { 1}
、しかしありません:そのような数を得るために2つのどちらかで1桁を変更することはできません。もしも
0.99999..。
{ 0.99999 …}
と 1 { 1}
実数を表すためには、等しくなければなりません。密な順序付けは、セットの2つの要素の間に厳密に新しい要素がない場合、2つの要素が等しいと見なされる必要があることを意味します。
一般化
0.999 … = 1という結果は、2つの方法で簡単に一般化されます。まず、有限の10進表記(同等に、無限の末尾の0)を持つすべての非ゼロの数値には、末尾に9が付いた対応物がたとえば、0.24999 …は0.25に等しく、考慮される特別な場合とまったく同じです。これらの数値は正確に小数であり、密度が高くなっています。
第二に、同等の定理は、各基数かに適用されるベース。たとえば、基数2(2進数システム)では0.111 …は1に等しく、基数3(3進数システム)では0.222 …は1に等しくなります。一般に、終了する基数bの式には、末尾が繰り返される対応物がb − 1に等しい数字。実際の分析の教科書は、0.999 …の例をスキップし、最初からこれらの一般化の一方または両方を提示する可能性が
1の代替表現は、非整数ベースでも発生します。たとえば、黄金比ベースでは、2つの標準表現は1.000 …と0.101010 …であり、隣接する1を含む表現は無限に一般に、1と2の間のほとんどすべての qについて、1の底q展開は数え切れないほど多く一方、底が1つしかないq(1より大きいすべての自然数を含む)はまだ数え切れないほど多くQの些細1.000以外1の膨張は、….この結果は、最初にすることによって得られたポール・エルデシュVilmos Komornik及び1998年に1990の周りに、ミクロスHorvathの、及びイシュトチュパオラLoretiが最小例えば塩基、決定Komornik-Loreti定数 q = 1.787231650 ….このベースでは、1 = 0.11010011001011010010110011010011 …; 数字は、繰り返されないThue-Morseシーケンスによって与えられます。
より広範囲な一般化は、最も一般的な位取り記数法に対応します。それらにも複数の表現があり、ある意味では困難はさらに悪化します。例:
でバランスのとれた三元系、
1 / 2 = 0.111 … = 1 111 ….
逆に階乗数システム(塩基2を使用して!、3!4!、…ポジションの後に小数点)= 1.000 1 … = 0.1234 ….
独自の表現の不可能性
これらすべての異なる数体系がいくつかの実数の複数の表現に苦しんでいることは、順序集合としての実数と辞書式順序の記号の無限文字列のコレクションとの間の根本的な違いに起因する可能性が実際、次の2つのプロパティが問題の原因です。
場合間隔の実数をれる分配二つの非空の部品にL、Rの各要素ように、Lは、(厳密に)以下のすべての要素よりもR、その後、いずれかのLが最大の要素が含まれているか、またはRは、最小の要素が含まれしかし、両方ではありません。
無限のコレクションの文字列任意の有限「アルファベット」から取られたシンボルのは、辞書的に注文した、二つの非空の部分に分割することができるL、R、のすべての要素ようにLは以下のすべての要素よりもRながら、Lは最大含まれています要素と Rには最小の要素が含まれます。実際、コレクションから要素の2つの有限の接頭辞(最初の部分文字列)p 1、p 2を取得して、それらが連続する値を持つ最終的な記号のみが異なるようにし、Lに対してすべての文字列のセットを取得するだけで十分です。そのプレフィックスを対応する最大であるコレクションでP 1、及びためR残り、対応する接頭辞少なくともあるコレクション内の文字列P 2。次いで、Lが始まる、最大要素を有するP 1ながら、すべての次の位置で最大の利用可能なシンボルを選択するRは、下記によって得られた最小の要素有するP 2を全ての位置で最小の記号です。
最初のポイントは、実数の基本的な特性から得られます。Lには上限があり、Rには下限があり、これらは簡単に等しいと見なされます。実数であるため、RまたはLのいずれかにありますが、LとRは互いに素であると想定されているため、両方ではありません。2番目のポイントは、p 1 = “”0″”、p 2 = “”1″”で取得された0.999 … / 1.000 …ペアを一般化します。実際、すべての位置に同じアルファベットを使用する必要はありません(たとえば、混基数システムを含めることができます)。または、可能な文字列の完全なコレクションを検討する必要はありません。唯一の重要なポイントは、各位置で有限のシンボルセット(前のシンボルに依存する場合もあります)を選択できること(これは最大および最小の選択を確実にするために必要です)、および任意の位置に対して有効な選択を行う必要があることです。結果は有効な無限文字列になります(したがって、「9」の無限の連続を禁止している間は、各位置に「9」を許可しないでください)。これらの仮定の下で、上記の引数は、文字列のコレクションから実数の間隔への順序保存マップが全単射になることはできないことを示しています。一部の数値はどの文字列にも対応しないか、一部は複数の文字列に対応します。 。
MarkoPetkovšekは、すべての実数に名前を付ける位置システムの場合、複数の表現を持つ実数のセットが常に密であることを証明しました。彼はその証明を「基本的なポイントセットトポロジーにおける有益な演習」と呼んでいます。これには、位置値のセットをストーンスペースとして表示し、それらの実際の表現が連続関数によって与えられていることに注意することが含まれます。
アプリケーション
1の表現としての0.999 …の1つのアプリケーションは、初等整数論で発生します。1802年、H。Goodwinは、分母が特定の素数である分数の循環小数表現における9の出現に関する観察結果を公開しました。例は次のとおりです。
1 / 7 = 0 142857および142 + 857 = 999。
1 / 73 = 0 01369863及び+ 9863 = 9999 0136。
E.ミディは、1836年に、現在ミディの定理と呼ばれるそのような分数に関する一般的な結果を証明しました。出版物はあいまいであり、彼の証明が直接0.999に関係していたかどうかは不明です… 0. b 1 b 2 b 3 …の形式の小数が正の整数であることが証明できる場合、それは0.999 …でなければならず、これが定理の9のソースになります。この方向の研究は、このような概念を動機付けることができる最大公約数、モジュラ算術、フェルマー素数、注文のグループ元素、および二次相反します。

位置は
1 / 4、 2 / 3で、そして1
カントール集合
実際の分析に戻ると、ベース3アナログ0.222 … = 1は、最も単純なフラクタルの1つであるカントール集合の3分の1の特性評価において重要な役割を果たします。
単位区間のポイントは、0と2の数字のみを使用して3値で表すことができる場合に限り、カントール集合に
表現のn番目の桁は、構築のn番目のステージでのポイントの位置を反映しています。例えば、ポイント
2 / 3は、それが最初に削除の右側に、その後、すべての削除の左側に位置するので、… 0.2または0.2000の通常の表現が与えられます。ポイント
1 / 3は、それが最初に削除の左側に、その後、すべての削除の右にあるので、…ない0.1としてではなく0.0222として表されます。
ナインを繰り返すことは、ゲオルク・カントールのさらに別の作品にも現れます。それらを考慮に入れて、1891年の対角論を小数展開に適用し、単位間隔の数えられないことの有効な証明を作成する必要がこのような証明は、実数の特定のペアが10進数の展開に基づいて異なることを宣言できる必要があるため、0.2や0.1999のようなペアを避ける必要があります…簡単な方法は、すべての数値を非終了の展開で表します。反対の方法では、9の繰り返しは除外されます。カントールの元の議論に近いかもしれない変形は、実際には基数2を使用し、基数3の展開を基数2の展開に変えることによって、カントール集合の数えられないことも証明できます。
教育における懐疑論
数学の学生は、0.999 …と1の等式を拒否することがよくこれは、外観の違いから、極限の概念に対する深い不安や、無限小の性質に関する意見の不一致に至るまでの理由からです。混乱の原因となる一般的な要因はたくさん
学生はしばしば「数は小数で一方向にしか表現できないという考えに精神的に取り組んでいます」。同じ数を表す2つの明らかに異なる小数を見ると、パラドックスのように見えます。これは、一見よく理解されている数1の出現によって増幅されます。
一部の学生は、「0.999 …」(または同様の表記)を、おそらく可変の不特定の長さを持つ、大きいが有限の9の文字列として解釈します。彼らが9の無限の文字列を受け入れる場合、彼らはまだ「無限に」最後の9を期待するかもしれません。
直感とあいまいな指導により、生徒はシーケンスの限界を、固定値ではなく一種の無限のプロセスと考えるようになります。これは、シーケンスが限界に達する必要がないためです。数列とその限界の違いを生徒が受け入れる場合、「0.999 …」は、その限界ではなく、数列を意味するものとして読むことができます。
これらのアイデアは、標準の実数のコンテキストでは誤解されていますが、一般的な数学的有用性のために、または0.999をよりよく理解するための有益な反例として、他の数値システムで有効なものも
これらの説明の多くは、大学生で遭遇した誤解のいくつかにつながる教育と認知の特徴を研究したデビッド・トールによって発見されました。大多数が最初に平等を拒否した理由を判断するために彼の学生にインタビューしたところ、彼は「学生は0.999 …を固定値ではなく、1に近づく一連の数値として考え続けました。それが1以下のできるだけ近い小数である」あるいは『どのように多くの場所に指定』」。
0.333を掛けるの基本引数… =
1 / 3、一部の学生は、最初の式の彼らの信念と第二の彼らの不信の間の紛争に直面したとき3によっては、まだ0.999 … = 1という消極的生徒を説得することができます最初の方程式を信じないようになるか、単にイライラするかのどちらかです。また、より洗練された方法は絶対確実ではありません。厳密な定義を完全に適用できる学生は、0.999を含む高度な数学の結果に驚いたときに、直感的な画像に頼ることができます。たとえば、ある実解析の学生0.333 … =ことを証明することができた
1 / 3を使用してsupremumの彼女は以前、長い分裂の理解に基づいて、1 <...定義は、その後0.999と主張しました。その他はまだあることを証明することができます
1 / 3 … = 0.333を、しかし、に直面している時に端数証明、「ロジック」は、数学的な計算に取って代わることを主張します。
ジョセフ・マズールは、「クラスで私が言ったことのほとんどすべてに挑戦したが、電卓に質問したことはなかった」彼の、そうでなければ素晴らしい微積分学の学生の話をします。 23のルート。学生は、9.99 … = 10という限定的な議論に不快感を覚え、「想像を絶する無限の成長過程」と呼んでいました。
Ed Dubinskyの数学学習のAPOS理論の一部として、彼と彼の共同研究者(2005)は、0.999 …を1からの距離が無限に小さい有限の不確定な文字列として考える学生は、「まだ完全なプロセス概念を構築していない」と提案しています。無限小数の」。0.999 …の完全なプロセス概念を持っている他の学生は、1のオブジェクト概念のように、そのプロセスを「オブジェクト概念」に「カプセル化」できない可能性があるため、プロセス0.999 …を表示します。オブジェクト1は互換性がありません。Dubinsky etal。また見にカプセル化のこの精神的な能力をリンク
1 / 3は、自身の右の数字として、全体としての自然数の集合に対処します。
文化現象
インターネットの台頭により、 30214290。
外部リンク
を聞く(50分)
![]()
このオーディオファイルは、2006年10月19日付けのの改訂版から作成されたもの
であり、その後の編集は反映され
(2006-10-19)( 音声ヘルプ ・
より多くの話された記事)
コモンズには0.999に関連するメディアがあります…。
.999999 … = 1?カットノット
なぜ0.9999 … = 1なのですか?
算術に基づく平等の証明
数学の認知に関するDavidTallの研究
実数を無限小数と考えることの何がそんなに悪いのでしょうか?
定理0.999 …にMetamath
![]()
数学ポータル”