1平面グラフ – 日本語百科事典辞書

1-planar_graph
トポロジカルグラフ理論、1平面グラフことができるグラフで描かでユークリッド平面それは単一の追加エッジを横切る各エッジは最大で1つの交点を有するようには。平面グラフの最も自然な一般化の1つである1平面グラフがそのように描画される場合、その描画は1平面グラフまたはグラフの1平面埋め込みと呼ばれます。
ヒーウッドグラフの1平面
図：6つのエッジには単一の交差があり、残りの15のエッジは交差し

コンテンツ
1 着色
2 エッジ密度
3 完全な多部グラフ
4 計算の複雑さ
5 一般化と関連する概念
6 参考文献
7 参考文献

着色
1平面グラフは、Ringel（1965）によって最初に研究され、最大7色で着色できることが示されました。その後、これらのグラフを着色するために必要な正確な色数は、最悪の場合、6色であることが示されました。の例完全グラフ K 6 1平面である、1-平面グラフは、6つの色を時々を必要とするかもしれないことを示しています。ただし、6色で十分であるという証明はもっと複雑です。

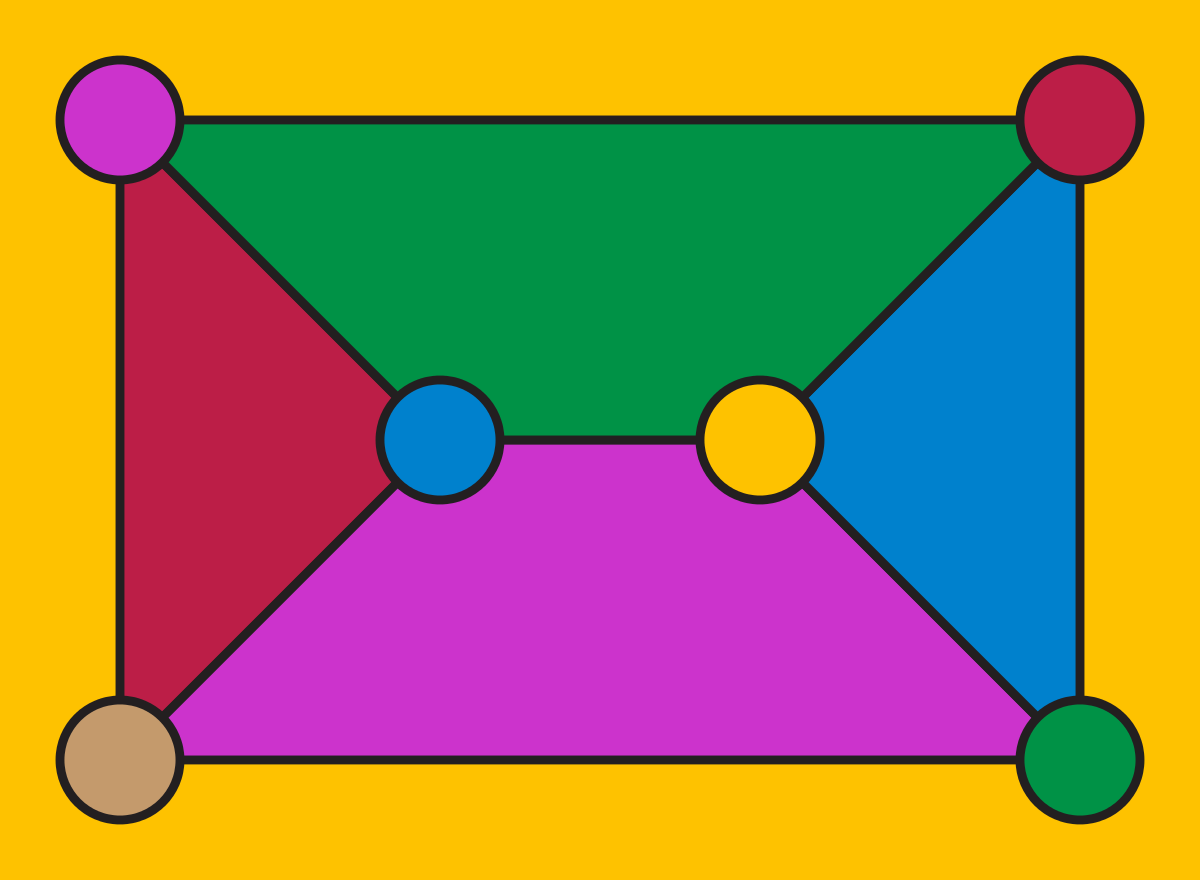
三角プリズムグラフの頂点と面を着色するには、6色が必要です
リンゲルの動機は、平面グラフの全体的な色付けのバリエーションを解決しようとすることでした。この方法では、2つの隣接する頂点が同じ色を持たず、2つの隣接する面が同じ色を持たないように、平面グラフの頂点と面を同時に着色します。色があり、互いに隣接する頂点と面が同じ色になることはありません。これは明らかに、4色の2つの互いに素なセットを使用して、与えられたグラフとその双対グラフに4色定理を別々に適用することにより、8色を使用して行うことができます。ただし、与えられた平面グラフの各頂点または面に頂点を持ち、与えられた平面グラフの隣接する特徴に対応するときはいつでも2つの補助グラフの頂点が隣接する補助グラフを形成することによって、より少ない色が得られる場合が着色頂点元の平面グラフの頂点面の着色に補助グラフ相当の。この補助グラフは1平面であり、このグラフから、リンゲルの頂点面の色付けの問題も6色で解決できる可能性がグラフK 6は、このように補助グラフとして形成することができないが、それでも頂点面着色問題も時々六色を必要とします。たとえば、色付けする平面グラフが三角柱の場合、11個の頂点と面には6色が必要です。これは、3つに単一の色を与えることができないためです。

エッジ密度
n個の頂点を持つすべての1平面グラフには、最大で4 n −8個のエッジがより強力に、各1平面図面には最大でn −2個の交差が交差する各エッジのペアから1つのエッジを削除すると、平面グラフが残ります。このグラフには、最大3 n − 6のエッジがあり、そこから、元の1平面グラフのエッジの数に4 n −8がバインドされます。ただし、平面グラフ（特定の頂点セット上のすべての最大平面グラフが互いに同じ数のエッジを持つ）とは異なり、最大1平面グラフ（保存中に追加のエッジを追加できないグラフ）が存在します。 1平面）4 n −8エッジよりも大幅に少ないエッジ。 1平面グラフの可能な最大エッジ数の4n − 8の境界を使用して、7つの頂点の完全グラフ K 7が1平面ではないことを示すことができます。これは、このグラフに21のエッジがあり、この場合、4 n − 8 = 20 <21です。
1平面グラフは、可能な限り最大の4 n − 8のエッジがある場合、最適な1平面グラフであると言われます。最適な1平面グラフの1平面埋め込みでは、交差していないエッジは必然的に四角形を形成します（すべての面が四角形である多面体グラフ）。すべての四角形は、その四角形の面のそれぞれに2つの対角線を追加することにより、このように最適な1平面グラフを生成します。すべて、最適な1平面グラフであることを以下のオイラー（その頂点の全ても有する程度を、このようなグラフの最小次数は6であり、そしてすべての最適な1平面グラフは度ちょうど6の少なくとも8つの頂点を有することこと）。さらに、すべての最適な1平面グラフは4頂点接続されており、そのようなグラフのすべての4頂点カットは、基礎となる四角形の分離サイクルです。
直線の1平面図面（つまり、各エッジが線分で表され、各線分が最大で1つの他のエッジと交差する図面）を持つグラフは、4 n −9のわずかに狭い境界を持ちます。無限に多くのグラフによって達成されるエッジの最大数。

完全な多部グラフ

1平面描画
カクテルパーティグラフ K 2，2，2，2
1平面完全グラフ、完全2部グラフ、およびより一般的には完全多部グラフの完全な分類が知られています。K 2、nの形式のすべての完全2部グラフは、K 1、1、nの形式のすべての完全3部グラフと同様に、1平面です。これらの無限の例のセットを除いて、完全な多分割1平面グラフはK 6、K 1，1，1，6、K 1，1，2，3、K 2，2，2，2、K1のみです。 1，1，2，2、およびそれらのサブグラフ。最小の非1平面完全多部グラフであるK 3，7、K 4，5、K 1，3，4、K 2，3，3、及びK 1，1，1，1，3。例えば、完全な二部グラフK 3，6は、それがのサブグラフであるため、1平面であるK 1，1，1，6が、K 3，7が1平面上ではありません。

計算の複雑さ
与えられたグラフが1平面であるかどうかをテストすることはNP完全であり、単一のエッジを追加することによって平面グラフから形成されたグラフや、制限された帯域幅のグラフでもNP完全のままです。。この問題は、循環的数またはツリーの深さによってパラメーター化された場合、固定パラメーターで扱いやすいため、これらのパラメーターが制限されている場合、多項式時間で解決される可能性が
平面グラフに関するFáryの定理とは対照的に、すべての1平面グラフがそのエッジに直線セグメントを使用して1平面で描画されるとは限りません。ただし、この方法で1平面の描画を直線化できるかどうかのテストは、多項式時間で実行できます。さらに、すべての3頂点接続された1平面グラフには、図面の外面の多くても1つのエッジに曲がりがある1平面図面がこの図面は、グラフの1平面埋め込みから線形時間で作成できます。 1-平面グラフは有界有する本の厚さを、が、を含むいくつか1平面グラフK 2，2，2，2は、少なくとも4本の厚さを有します。
1平面グラフが持つローカルツリー幅有界（線形）関数が存在することを意味し、Fのようにその直径の1平面グラフD HAVEツリー幅最大でF（D）。同じプロパティは、エッジごとの交差の数が制限されている境界のある属の表面に埋め込むことができるグラフについて、より一般的に当てはまります。それらはまたセパレーター、頂点の小さなセットを持っており、それを取り除くとグラフは接続されたコンポーネントに分解され、そのサイズはグラフ全体のサイズの一定の割合になります。これらの特性に基づいて、近似アルゴリズムを設計するためのベイカーの手法など、平面グラフの多数のアルゴリズムを1平面グラフに拡張できます。例えば、この方法リード多項式時間近似スキームのための最大独立集合1平面グラフ。

一般化と関連する概念
類似したグラフのクラスouterplanarグラフ1平坦ために呼び出される外側-1-平面グラフ。これらは、ディスクの境界に頂点があり、エッジごとに最大1つの交差があるディスクに描画できるグラフです。これらのグラフは、直定規と直角の交差で常に（外側1平面の方法で）描画できます。使用することにより、動的プログラミングにSPQRツリー所与のグラフの、それが外1平面内にあるかどうかをテストすることが可能である線形時間。グラフの3つの接続されたコンポーネント（SPQRツリーのノード）は、閉路グラフ、結合グラフ、および4頂点の完全グラフのみで構成できます。これにより、外側の1平面グラフも平面になります。そして持っているツリー幅を最も三時。
1平面グラフには、4マップグラフが含まれます。これは、平面内の領域の隣接から形成されたグラフで、最大4つの領域が任意の点で交わっています。逆に、すべての最適な1平面グラフは4マップグラフです。ただし、最適な1平面グラフではない1平面グラフは、マップグラフではない場合が
1平面グラフは、k平面グラフに一般化されています。これは、各エッジが最大k回交差するグラフです（0平面グラフは正確に平面グラフです）。リンゲルは、Gの局所交差数を最小の非負の整数kと定義し、Gがk平面図を持つようにしました。ローカル交差数は、最適な図面のエッジの交差グラフの最大次数であり、厚さ（エッジを分割できる平面グラフの最小数）は、の交差グラフの色数として見ることができます。適切な図では、ブルックスの定理から、厚さは最大で1にローカル交差数を加えたものであることがわかります。 Kと-planarグラフN頂点は高々有するO（K 1/2 N）エッジ、及びツリー幅O（（KN）1/2）。浅いマイナーのK -planarグラフで、深さとD、（2自体であるD + 1）kを1平面グラフとの浅い未成年者に、-planarグラフをK -planarグラフでもあるスパースグラフ、1平面グラフとk平面グラフが拡張を制限していることを意味します。
非平面グラフは、グラフの描画で交差するエッジのペアの最小数である交差数によってパラメータ化することもできます。交差数kのグラフは、必然的にk平面ですが、必ずしもその逆ではありません。たとえば、ヒーウッドグラフの交差数は3ですが、3つの交差がすべてグラフの同じエッジで発生する必要はないため、1平面であり、実際には同時に最適化する方法で描画できます。交差点の総数とエッジごとの交差点。
非平面グラフに関連するもう1つの概念は、グラフの歪度です。これは、グラフを平面にするために削除する必要のあるエッジの最小数です。

参考文献
^ Ringel、Gerhard（1965）、 “”Ein Sechsfarbenproblem auf der Kugel””、Abhandlungen aus dem MathematischenSeminarderUniversitätHamburg（in German）、29（1–2）：107–117、doi：10.1007 / BF02996313、MR 0187232、S2CID 123286264。
^ Borodin、OV（1984）、「平面グラフの頂点面の色付けと1平面グラフの色付けに関するリンゲル問題の解決」、Metody Diskretnogo Analiza（41）：12–26、108、MR 0832128
。
^ アルバートソン、マイケルO。; Mohar、Bojan（2006）、「局所平面グラフの頂点と面の着色」（PDF）、Graphs and Combinatorics、22（3）：289–295、doi：10.1007 / s00373-006-0653-4、MR 2264852、S2CID 1028234   。
^ Schumacher、H。（1986）、 “”Zur Struktur 1-planarer Graphen””、Mathematische Nachrichten（ドイツ語）、125：291–300、doi：10.1002 / mana.19861250122、MR 0847368
。
^ Czap、Július; Hudák、Dávid（2013）、「1平面グラフの描画と分解について」、Electronic Journal of Combinatorics、20（2）、P54、doi：10.37236 / 2392 ^ ブランデンブルク、フランツジョセフ; エプスタイン、デビッド; グライスナー、アンドレアス; グッドリッチ、マイケルT。; ハナウアー、カトリン; Reislhuber、Josef（2013）、「最大1平面グラフの密度について」、Didimo、Walter; パトリニャーニ、マウリツィオ（編）、Proc。20thInt。症状。グラフ描画 ^ Czap、Július; Hudák、Dávid（2012）、「完全な多部グラフの1平面性」、離散応用数学、160（4–5）：505–512、doi：10.1016 / j.dam.2011.11.014、MR 2876333
。
^ 鈴木裕介（2010）、「最大1平面グラフの再埋め込み」、SIAM Journal on Discrete Mathematics、24（4）：1527–1540、doi：10.1137 / 090746835、MR 2746706
。
^ Didimo、Walter（2013）、「直線1平面グラフ図面の密度」、情報処理レター、113（7）：236–240、doi：10.1016 / j.ipl.2013.01.013、MR 3017985
。
^ グリゴリエフ、アレクサンダー; Bodlaender、Hans L.（2007）、「エッジごとの交差がほとんどない埋め込み可能なグラフのアルゴリズム」、Algorithmica、49（1）：1–11、doi：10.1007 / s00453-007-0010-x、hdl：1874/17980、MR 2344391、S2CID 8174422
  。
^ Korzhik、Vladimir P。; Mohar、Bojan（2009）、「1-液浸の最小障害物と1-平面性テストの硬度」、Tollis、Ioannis G。; Patrignani、Maurizio（eds。）、Graph Drawing：16th International Symposium、GD 2008、Heraklion、Crete、Greece、September 21-24、2008、Revised Papers、Lecture Notes in Computer Science、5417、Springer、pp。302–312、arXiv：1110.4881、doi：10.1007 / 978-3-642-00219-9_29、S2CID 13436158
。
^ カベッロ、セルジオ; Mohar、ボヤン（2012）は、平面グラフに一つのエッジを追加ハード数と1-平面と交差することができる、arXivの：1203.5944、Bibcode：2012arXiv1203.5944Cを
。2010年の第17回ACM計算幾何学シンポジウムの論文の拡張版。
^ バニスター、マイケルJ。; カベッロ、セルジオ; Eppstein、David（2013）、「1- planarityのパラメータ化された複雑性」、Algorithms and Data Structures Symposium（WADS 2013）、arXiv：1304.5591、Bibcode：2013arXiv1304.5591B、doi：10.7155 / jgaa.00457、S2CID 4417962
。
^ Eggleton、Roger B.（1986）、「グラフの直線図」、Utilitas Mathematica、29：149–172、MR 0846198
。
^ Thomassen、Carsten（1988）、「グラフの直線図」、Journal of Graph Theory、12（3）：335–341、doi：10.1002 / jgt.3190120306、MR 0956195
。
^ ホン、ソクヒ; イーデス、ピーター; リオッタ、ジュゼッペ; Poon、Sheung-Hung（2012）、「1平面グラフのFáryの定理」、Gudmundsson、Joachim; メストレ、ジュリアン; Viglas、Taso（eds。）、Computing and Combinatorics：18th Annual International Conference、COCOON 2012、Sydney、Australia、August 20-22、2012、Proceedings、Lecture Notes in Computer Science、7434、Springer、pp。335–346、doi：10.1007 / 978-3-642-32241-9_29 ^ アラム、Md。Jawaherul; Brandenburg、Franz J。; Kobourov、Stephen G.（2013）、「3接続1平面グラフの直線グリッド描画」、グラフ描画：第21回国際シンポジウム、GD 2013、フランス、ボルドー、2013年9月23〜25日、改訂された選択された論文（ PDF）、コンピュータサイエンス、中講義ノート8242、頁83-94、。DOI：10.1007 / 978-3-319-03841-4_8 。
^ ベコス、マイケルA。; ブルックドルファー、ティル; カウフマン、マイケル; Raftopoulou、Chrysanthi（2015）、「1-平面グラフは一定の本の厚さを持っています」、アルゴリズム– ESA 2015、コンピュータサイエンスのレクチャーノート、9294、Springer、pp。130–141、doi：10.1007 / 978-3-662-48350 -3_12 ^ ベコス、マイケル; カウフマン、マイケル; Zielke、Christian（2015）、「SAT解決の観点からの本の埋め込み問題」、Proc。グラフ描画とネットワーク可視化に関する第23回国際シンポジウム（GD 2015）、113〜125ページ ^ Grigoriev＆Bodlaender（2007）。GrigorievとBodlaenderは、既知の1平面埋め込みを使用したグラフについてのみ結果を示し、交差が4次の頂点に置き換えられた埋め込みの平面化のツリー分解を使用します。ただし、それらのメソッドは、元の1平面グラフの制限されたローカルツリー幅を直接意味し、埋め込みを知らなくてもベイカーのメソッドを直接適用できるようにします。
^ Dehkordi、Hooman Reisi; Eades、Peter（2012）、「すべての外側1平面グラフには直角の交差図があります」、International Journal of Computational Geometry＆Applications、22（6）：543–557、doi：10.1142 / S021819591250015X、MR 3042921
。
^ ホン、ソクヒ; イーデス、ピーター; 加藤直樹; リオッタ、ジュゼッペ; シュバイツァー、パスカル; 鈴木裕介（2013）、「外部1平面性をテストするための線形時間アルゴリズム」、Wismath、Stephen; ウォルフ、アレクサンダー（編）、第21回国際シンポジウム、GD 2013、ボルドー、フランス、月23-25、2013、改訂選択した論文、コンピュータサイエンス、中講義ノート8242、頁71-82、。DOI：10.1007 / 978- 3-319-03841-4_7 ^ アウアー、クリストファー; バッハマイヤー、クリスチャン; Brandenburg、Franz J。; グライスナー、アンドレアス; ハナウアー、カトリン; ニューワース、ダニエル; Reislhuber、Josef（2013）、「線形時間での外側の1平面グラフの認識」、Wismath、Stephen; Wolff、Alexander（eds。）、21st International Symposium、GD 2013、Bordeaux、France、September 23-25、2013、Revised Selected Papers、Lecture Notes in Computer Science、8242、pp。107–118、doi：10.1007 / 978- 3-319-03841-4_10 ^ Chen、Zhi-Zhong; グリニ、ミケランジェロ; Papadimitriou、Christos H.（2002）、「マップグラフ」、Journal of the ACM、49（2）：127–138、arXiv：cs / 9910013、doi：10.1145 / 506147.506148、MR 2147819、S2CID 2657838
  。
^ カイネン、ポール（1973）、「グラフの厚さと粗さ」、Abh。算数。Sem。大学ハンブルク、39：88–95、doi：10.1007 / BF02992822、MR 0335322、S2CID 121667358
  。
^ パッハ、ヤノス; Tóth、Géza（1997）、「エッジごとに交差がほとんどないグラフ」、Combinatorica、17（3）：427–439、doi：10.1007 / BF01215922、MR 1606052、S2CID 20480170
  。
^ ドゥイモビッチ、ビーダ; エプスタイン、デビッド; Wood、David R.（2015）、「属、樹木幅、およびローカル交差数」、Proc。グラフ描画とネットワーク視覚化に関する第23回国際シンポジウム（GD 2015）、77〜88ページ、arXiv：1506.04380、Bibcode：2015arXiv150604380D ^ Nešetřil、Jaroslav ; Ossona de Mendez、Patrice（2012）、Sparsity ：Graphs、Structures、and Algorithms、Algorithms and Combinatorics、28、Springer、Theorem 14.4、p。321、doi：10.1007 / 978-3-642-27875-4、ISBN
978-3-642-27874-7、MR 2920058。

参考文献
コブロフ、スティーブン; リオッタ、ジュゼッペ; Montecchiani、Fabrizio（2017）、 ” Annotated bibliography on 1- planarity “、Computer Science Review、25：49–67、arXiv：1703.02261、Bibcode：2017arXiv170302261K、doi：10.1016 / j.cosrev.2017.06.002、S2CID 7732463”