A *検索アルゴリズム

A*_search_algorithm
A *（「A-star」と発音）は、グラフ走査およびパス検索 アルゴリズムであり、その完全性、最適性、および最適な効率により、コンピューターサイエンスの多くの分野でよく使用されます。 1つの大きな実用上の欠点は、 O （（ NS）。
{O（b ^ {d}）}
生成されたすべてのノードをメモリに格納するため、スペースが複雑になります。したがって、実際の旅行ルーティングシステムでは、一般に、グラフを前処理してパフォーマンスを向上させることができるアルゴリズムや、メモリに制限のあるアプローチよりも優れています。ただし、多くの場合、A *が依然として最良のソリューションです。
クラス
検索アルゴリズム
データ構造
グラフ
最悪の場合の パフォーマンス O （（| E |
）。= O（（NS
NS）。
{O（| E |）= O（b ^ {d}）}
最悪の場合の スペースの複雑さ O （（| V |
）。= O（（NS
NS）。
{O（| V |）= O（b ^ {d}）}
スタンフォード研究所（現在のSRIインターナショナル）のPeter Hart、Nils Nilsson、Bertram Raphaelは、1968年に最初にアルゴリズムを公開しました。これはダイクストラのアルゴリズムの拡張と見なすことができます。A *は、ヒューリスティックを使用して検索をガイドすることにより、パフォーマンスを向上させます。

コンテンツ
1 歴史
2 説明
2.1 擬似コード 2.2 例 2.3 実装の詳細 2.4 特殊なケース
3 プロパティ
3.1 終了と完全性 3.2 許容性 3.3 最適な効率
4 限界のあるリラクゼーション
5 複雑
6 アプリケーション
7 他のアルゴリズムとの関係
8 バリアント
9 も参照してください
10 ノート
11 参考文献
12 参考文献
13 外部リンク

歴史

  A *は、Shakey theRobotの経路計画に取り組んでいる研究者によって発明されました。
A *は、独自のアクションを計画できる移動ロボットの構築を目的としたShakeyプロジェクトの一環として作成されました。Nils Nilssonは当初、Shakeyの経路計画にGraphTraverserアルゴリズムを使用することを提案しました。グラフトラバーサーは、ノードnからゴールノードまでの推定距離であるヒューリスティック関数h（n）によってガイドされます。開始ノードからnまでの距離であるg（n）を完全に無視します。バートラム・ラファエルは、合計g（n）+ h（n）を使用することを提案しました。 Peter Hartは、ヒューリスティック関数の許容性と一貫性と呼ばれる概念を発明しました。A *は元々、パスのコストがそのコストの合計である場合に最小コストのパスを見つけるために設計されましたが、A *を使用して、コスト代数の条件を満たす問題の最適なパスを見つけることができることが示されています。
元の1968年のA *論文には、ヒューリスティック関数が一貫していてA *のタイブレークルールが適切に選択されている場合、A *のようなアルゴリズムはA *よりも少ないノードを拡張できないという定理が含まれていました。一貫性は必要ないと主張する「修正」が数年後に公開されましたが、これはA *の最適性（現在は最適効率と呼ばれています）に関するDechter andPearlの決定的な研究で誤りであることが示されました。許容できるが一貫性のないヒューリスティックを使用したA *の、代替のA *のようなアルゴリズムよりも任意に多くのノードを拡張します。

説明
A *は、情報に基づく検索アルゴリズム、つまり最良優先探索です。つまり、重み付きグラフの観点から定式化されます。グラフの特定の開始ノードから開始して、最小の特定の目標ノードへのパスを見つけることを目的としています。コスト（最短移動距離、最短時間など）。これは、開始ノードで発生するパスのツリーを維持し、その終了基準が満たされるまで、一度に1つのエッジでそれらのパスを拡張することによって行われます。
メインループの各反復で、A *はどのパスを拡張するかを決定する必要がこれは、パスのコストと、パスをゴールまで延長するために必要なコストの見積もりに基づいて行われます。具体的には、A *は最小化するパスを選択します （（ ）。= （（ ）。+ （（ ）。
{f（n）= g（n）+ h（n）}
  ここで、nはパス上の次のノード、g（n）は開始ノードからnまでのパスのコスト、h（n）はnからゴールまでの最も安いパスのコストを推定するヒューリスティック関数です。A *は、延長することを選択したパスが開始からゴールまでのパスである場合、または延長する資格のあるパスがない場合に終了します。ヒューリスティック関数は問題固有です。ヒューリスティック関数が許容可能である場合、つまり、目標に到達するための実際のコストを過大評価しない場合、A *は開始から目標までの最小コストのパスを返すことが保証されます。
A *の一般的な実装では、優先度キューを使用して、拡張する最小（推定）コストノードの繰り返し選択を実行します。この優先キューは、オープンセットまたはフリンジと呼ばれます。アルゴリズムの各ステップで、f（x）値が最も低いノードがキューから削除され、それに応じて隣接ノードのf値とg値が更新され、これらの隣接ノードがキューに追加されます。アルゴリズムは、削除されたノード（つまり、すべてのフリンジノードの中でf値が最も低いノード）がゴールノードになるまで続きます。許容可能なヒューリスティックでは、目標のhがゼロであるため、その目標のf値は最短経路のコストでも
これまでに説明したアルゴリズムでは、最短パスの長さのみが示されます。ステップの実際のシーケンスを見つけるために、アルゴリズムを簡単に修正して、パス上の各ノードがその前のノードを追跡できるようにすることができます。このアルゴリズムが実行された後、終了ノードはその先行ノードを指し、以下同様に、あるノードの先行ノードが開始ノードになるまで続きます。
例として、地図上で最短ルートを検索する場合、h（x）はゴールまでの直線距離を表す場合がこれは、物理的に任意の2点間の最短距離であるためです。ビデオゲームのグリッドマップの場合、使用可能な一連の動き（4方向または8方向）に応じて、マンハッタン距離またはオクタイル距離を使用する方が適切です。

  ランダムに生成された迷路の周りをナビゲートする*パスファインディングアルゴリズム

メディアを再生する
グラフ上の2点間のパスを見つけるためのA *検索の図。
場合ヒューリスティック 時間満たす追加の条件H（X）≤ D（X、Y）+ H（Y）毎にエッジに対する（X、Y）（グラフdはそのエッジの長さを示す）、次いでHが呼び出され単調、または一貫性。一貫ヒューリスティックで、Aは、*複数回任意のノードを処理せずに最適な経路を見つけることが保証され、Aは、*実行するのと同じであるダイクストラ法を用いて低コストの D」（X、Y）= D（X、Y）+ H（y）− h（x）。

擬似コード
次の擬似コードは、アルゴリズムを説明しています。
関数 reconstruct_path （cameFrom 、 現在の） total_path ：= {現在} ながら 電流 で cameFrom 。キー：
current ：= cameFrom
total_path 。prepend （current ） return total_path// A *はスタートからゴールまでのパスを見つけます。// hはヒューリスティック関数です。h（n）は、ノードnから目標に到達するためのコストを見積もります。function A_Star （start 、 goal 、 h ） //（再）展開する必要がある可能性のある検出されたノードのセット。 //最初は、開始ノードのみが認識されています。 //これは通常、ハッシュセットではなく、最小ヒープまたは優先度キューとして実装されます。 openSet ：= {start} //ノードnの場合、cameFrom は、開始から 現在既知のn までの最も安価なパスで//その直前のノードです。cameFrom ：= 空のマップ
//ノードnの場合、gScore は、現在既知の開始からnまでの最も安価なパスのコストです。 gScore ：= マップ と デフォルト 値 の インフィニティ gScore ：= 0 //ノードnの場合、fScore ：= gScore + h（n）。fScore は、 // nを通過する場合、開始から終了までのパスがどれだけ短くなるかについての 現在の最良の推測を表します。fScore ：= マッピング と デフォルト 値 の 無限 fScore ：= H （開始） ながら openSetが され ていない 空
//この操作はOで発生する可能性openSetが最小ヒープ又は優先度キューである場合、（1）時間
電流 ：= ノードにopenSet有する最低fScore []の値があれば、現在=目標リターンreconstruct_path （cameFrom 、現在）
openSet 。削除（現在の）
のための 各 ネイバー の 現在の
隣に電流から// D（現在、ネイバー）エッジの重みである
// tentative_gScoreは貫通電流開始から隣への距離である
tentative_gScore = gScore + D （current 、 neighbor ）
if tentative_gScore < gScore
//このneighborへのパスは以前のパスよりも優れています。それを記録する！
cameFrom ：= 現在
gScore ：= tentative_gScore
fScore ：= gScore + H （隣接）
する場合 、隣接 しない で openSet
openSet 。追加（隣人） //オープンセットは空ですが、目標に到達しませんでした リターン エラー
備考：この擬似コードでは、ノードが1つのパスで到達し、openSetから削除され、その後、より安価なパスで到達すると、openSetに再び追加されます。これは、ヒューリスティック関数が許容できるが一貫性がない場合に、返されるパスが最適であることを保証するために不可欠です。ヒューリスティックが一貫している場合、ノードがopenSetから削除されると、そのノードへのパスが最適であることが保証されるため、ノードに再び到達した場合、テスト ‘tentative_gScore
  ロボット
動作計画問題で開始ノードから目標ノードへのパスを見つけるためのA *検索の図
。空の円は開集合内のノード、つまり探索されていないノードを表し、塗りつぶされた円
は閉集合内に閉じた各ノードの色は、ゴールからの距離を示します。緑が多いほど、近くになります。最初にA *がゴールの方向に直線で移動しているのを見ることができ、次に障害物にぶつかると、オープンセットからノードを通る代替ルートを探索します。
参照： ダイクストラのアルゴリズム

例
ノードが道路に接続された都市であり、h（x）がターゲットポイントまでの直線距離である場合のA *アルゴリズムの動作例は次のとおりです。

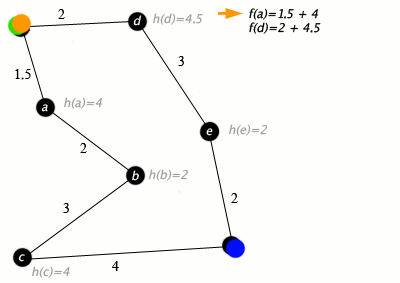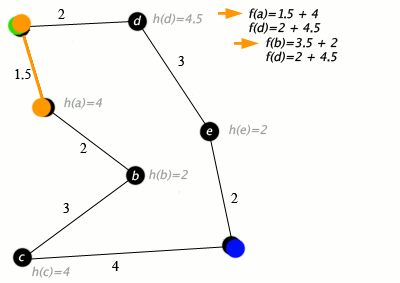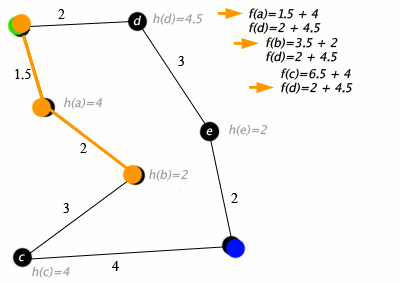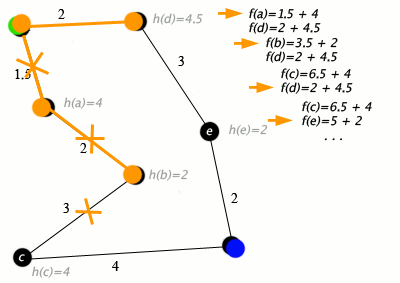
キー：緑：開始; 青：ゴール; オレンジ：訪問
A *アルゴリズムには、実際のアプリケーションもこの例では、エッジは鉄道であり、h（x）はターゲットまでの大円距離（球上で可能な最短距離）です。アルゴリズムは、ワシントンDCとロサンゼルスの間のパスを検索しています。

実装の詳細
A *実装のパフォーマンスに大きな影響を与える可能性のある、いくつかの単純な最適化または実装の詳細が注意すべき最初の詳細は、優先キューがタイを処理する方法が、状況によってはパフォーマンスに大きな影響を与える可能性があることです。同点が壊れてキューがLIFOのように動作する場合、A *は等しいコストパス間で深さ優先探索のように動作します（複数の等しく最適なソリューションの探索を回避します）。
検索の最後にパスが必要な場合、各ノードでそのノードの親への参照を保持するのが一般的です。検索の最後に、これらの参照を使用して最適なパスを復元できます。これらの参照が保持されている場合は、同じノードが優先度キューに複数回表示されないことが重要になる可能性があります（各エントリはノードへの異なるパスに対応し、それぞれ異なるコストがかかります）。ここでの標準的なアプローチは、追加しようとしているノードが優先キューにすでに表示されているかどうかを確認することです。含まれている場合、優先度と親のポインタは、低コストのパスに対応するように変更されます。標準のバイナリヒープベースの優先度キューは、その要素の1つを検索する操作を直接サポートしていませんが、要素をヒープ内の位置にマップするハッシュテーブルで拡張できるため、この優先度の低下操作をで実行できます。対数時間。あるいは、フィボナッチヒープは、一定の償却時間内に同じ優先度の低下操作を実行できます。

特殊なケース
均一コスト探索アルゴリズムの別の例としてのダイクストラのアルゴリズムは、A *の特殊なケースと見なすことができます。 （（ ）。= 0
{h（x）= 0}

 すべてのxに対して。 非常に大きな値で初期化されたグローバルカウンターCがあることを考慮することにより、A *を使用して一般的な深さ優先探索を実装できます。ノードを処理するたびに、新しく検出されたすべてのネイバーにCを割り当てます。単一の割り当てごとに、カウンターCを1つ減らします。したがって、ノードが早期に発見されるほど、そのノードは高くなります （（ ）。
{h（x）}

 価値。ダイクストラのアルゴリズムと深さ優先探索の両方を、 （（ ）。
{h（x）}

  各ノードの値。

プロパティ

終了と完全性
負でないエッジの重みを持つ有限グラフでは、A *は終了することが保証され、完全です。つまり、解決策（開始から目標までのパス）が存在する場合は常にそれを見つけます。有限の分岐係数とゼロから離れて制限されているエッジコストを持つ無限グラフ（ （（ 、 y ）。
>> ε >> 0 { textstyle d（x、y）> varepsilon> 0}
varepsilon >0}””>
  いくつかの固定 ε { varepsilon}

 ）、A *は、解決策が存在する場合にのみ終了することが保証されています。

許容性
最適解を返すことが保証されている場合、検索アルゴリズムは許容できると言われます。A *で使用されるヒューリスティック関数が許容される場合、A *は許容されます。これの直感的な「証拠」は次のとおりです。
A *が検索を終了すると、開始から目標までのパスが見つかりました。実際のコストは、開いているノード（ノードの {f}

 価値）。ヒューリスティックが許容できる場合、これらの推定値は楽観的です（完全ではありません。次の段落を参照）。したがって、A *は、既存のノードよりも安価なソリューションにつながる可能性がないため、これらのノードを安全に無視できます。言い換えれば、A *は、開始から目標までの低コストのパスの可能性を見逃すことはないため、そのような可能性がなくなるまで検索を続けます。
実際の証明は、 {f}

 ヒューリスティックが許容できる場合でも、開いているノードの値が楽観的であるとは限りません。これは、 {g}

  開いているノードの値が最適であるとは限らないため、合計 + {g + h}

  楽観的であるとは限りません。

最適な効率
アルゴリズムAは、Pのすべての問題PおよびAltsのすべてのアルゴリズムA ‘について、Pを解く際にAによって拡張されたノードのセットがサブセットである場合、一連の問題Pに対する一連の代替アルゴリズムAltsに関して最適に効率的です（おそらく等しい）Pを解く際にA ‘によって拡張されたノードのセットの。A*の最適効率の決定的な研究は、RinaDechterとJudeaPearlによるものです。彼らは、AltsとPのさまざまな定義を、A *のヒューリスティックと組み合わせて、単に許容可能であるか、一貫性と許容性の両方であると考えました。彼らが証明した最も興味深い肯定的な結果は、一貫したヒューリスティックを備えたA *が、すべての「非病理学的」探索問題で許容されるすべてのA *のような探索アルゴリズムに関して最適に効率的であることです。大まかに言えば、彼らの非病理学的問題の概念は、私たちが現在「タイブレークまで」と意味しているものです。この結果は、A *のヒューリスティックが許容できるが、一貫性がない場合には当てはまりません。その場合、DechterとPearlは、いくつかの非病理学的問題でA *よりも任意に少ないノードを拡張できる許容可能なA *のようなアルゴリズムが存在することを示しました。
最適な効率は、ノード拡張の数（A *のメインループの反復数）ではなく、拡張されたノードのセットに関するものです。使用されているヒューリスティックが許容できるが一貫性がない場合、ノードがA *で何度も拡張される可能性があり、最悪の場合は指数関数的に拡張されます。このような状況では、ダイクストラのアルゴリズムはA *を大幅に上回る可能性が

限界のあるリラクゼーション

  一貫性のあるヒューリスティックの5.0（=ε）倍のヒューリスティックを使用し、次善のパスを取得する*検索 許容基準は最適なソリューションパスを保証しますが、A *が最適なパスを見つけるためにすべての同等に価値のあるパスを調べる必要があることも意味します。おおよその最短経路を計算するために、許容基準を緩和することにより、最適性を犠牲にして検索を高速化することができます。多くの場合、この緩和を制限して、解のパスが最適な解のパスの（1 + ε）倍より悪くないことを保証できるようにします。この新しい保証は、ε許容と呼ばれます。
いくつかのε許容アルゴリズムがあります：
加重A * /静的加重。場合にはH（nは）許容ヒューリスティック関数であり、Aの加重バージョンの*いずれかを使用し検索H W（nは）= εH A（N）、ε > 1ヒューリスティック関数として、及び実行通常どおりのA *検索（展開されるノードが少ないため、最終的にはh aを使用するよりも高速に実行されます）。したがって、検索アルゴリズムによって検出されたパスのコストは、グラフ内の最小コストのパスの最大ε倍になる可能性が
動的重み付けはコスト関数を使用します （（ ）。= （（ ）。 + （（ 1+ ε w（（ ）。
）。 （（ ）。
{f（n）= g（n）+（1+ varepsilon w（n））h（n）}

 、 どこ w （（ ）。 = {{ 1 − （（ ）。 （（ ）。
≤ 0
それ以外は
{w（n）= { begin {cases} 1-{ frac {d（n）} {N}}＆d（n） leq N \ 0＆{ text {otherwise}} end {cases }}}

 、 そしてどこに （（ ）。
{d（n）}

 は検索の深さであり、Nはソリューションパスの予想される長さです。
Sampled Dynamic Weighting は、ノードのサンプリングを使用して、ヒューリスティックエラーをより適切に推定およびバイアス除去します。 ε ∗ {A _ { varepsilon} ^ {*}}

 。は2つのヒューリスティック関数を使用します。1つ目はFOCALリストで、候補ノードを選択するために使用され、2つ目のh Fは、FOCALリストから最も有望なノードを選択するために使用されます。
ε 機能を有する選択ノード （（ ）。+（（ ）。
{Af（n）+ Bh_ {F}（n）}

 、ここで、AとBは定数です。ノードを選択できない場合、アルゴリズムは関数でバックトラックします （（ ）。+（（ ）。
{Cf（n）+ Dh_ {F}（n）}

 、ここで、CとDは定数です。
AlphA * は、最近拡張されたノードを優先することにより、深さ優先探索を促進しようとします。AlphA *はコスト関数を使用します α（（ ）。 = （（ 1+ w α（（ ）。
）。 （（ ）。
{f _ { alpha}（n）=（1 + w _ { alpha}（n））f（n）}

 、 どこw α（（ ）。 = {{
λ （（ π（（ ）。 ）。 ≤ （（ 〜
）。 Λ それ以外は
{w _ { alpha}（n）= { begin {cases} lambda＆g（ pi（n）） leq g（{ tilde {n}}）\ Lambda＆{ text {otherwise }} end {cases}}}

 、ここで、λとΛは次の定数です。λ ≤ Λ
{ lambda leq Lambda}

 、πは、（N）の親であるN、及びNは最近拡張ノードです。

複雑
A *の時間計算量は、ヒューリスティックに依存します。無制限の探索空間の最悪の場合、展開されるノードの数は、解の深さ（最短経路）で指数関数的になります。d：O（b d）、ここで、bは分岐係数（状態ごとの後続の平均数）です。 ）。これは、目標状態がまったく存在し、開始状態から到達可能であることを前提としています。そうではなく、状態空間が無限大である場合、アルゴリズムは終了しません。
良いヒューリスティックは、A *は離れて、多くのプルーニングすることができますので、ヒューリスティック機能は、A *サーチの実用性能に大きな影響を与えたB Dの無知検索が拡大することにノードを。その品質は、有効な分岐係数b *で表すことができます。これは、展開によって生成されたノードの数Nと解の深さを測定し、解くことによって、問題のインスタンスに対して経験的に決定できます。 +1 = 1+ ∗ + （（ ∗）。2 + ⋯ +（（ ∗）。 。
{N + 1 = 1 + b ^ {*} +（b ^ {*}）^ {2} + dots +（b ^ {*}）^ {d}。}
  優れたヒューリスティックは、有効な分岐係数が低いものです（最適なのはb * = 1です）。
探索空間がツリーであり、単一の目標状態があり、ヒューリスティック関数hが次の条件を満たす場合、時間計算量は多項式です。
| （（ ）。
− ∗（（ ）。 | = O （（ ログ ∗（（ ）。 ）。 {| h（x）-h ^ {*}（x）| = O（ log h ^ {*}（x））}
  ここで、h *は最適なヒューリスティックであり、xからゴールに到達するための正確なコストです。言い換えると、hの誤差は、xからゴールまでの真の距離を返す「完全なヒューリスティック」h *の対数よりも速く大きくなることはありません。
A *のスペースの複雑さは、生成されたすべてのノードをメモリに保持するため、他のすべてのグラフ検索アルゴリズムのスペースの複雑さとほぼ同じです。実際には、これがA *検索の最大の欠点であることが判明し、反復的な深化A *、メモリ制限A *、SMA *などのメモリ制限ヒューリスティック検索の開発につながります。

アプリケーション
A *は、ビデオゲームなどのアプリケーションで一般的なパスファインディングの問題によく使用されますが、元々は一般的なグラフ走査アルゴリズムとして設計されました。これは問題を含む、多様な問題にアプリケーションを見出す解析使用して確率的文法でNLPを。他のケースには、オンライン学習による情報検索が含まれます。

他のアルゴリズムとの関係
A *を貪欲な最良優先探索アルゴリズムと区別するのは、すでに移動したコスト/距離g（n）を考慮に入れることです。
ダイクストラのアルゴリズムのいくつかの一般的な変形は、ヒューリスティックなA *の特殊なケースと見なすことができます。 （（ ）。= 0
{h（n）= 0}

 すべてのノードに対して。 次に、ダイクストラとA *はどちらも動的計画法の特殊なケースです。 A *自体は、分枝限定法の一般化の特殊なケースです。

バリアント
いつでもA *
ブロックA * フィールドD *
フリンジ
フリンジセービングA *（FSA *）
一般化されたアダプティブA *（GAA *）
インクリメンタルヒューリスティック検索
削減されたA *
反復的な深化A *（IDA *）
ジャンプポイント検索
生涯計画A *（LPA *）
新しい双方向A *（NBA *）
簡略化されたメモリ制限A *（SMA *）
シータ*
A *は、双方向検索アルゴリズムに適合させることもできます。停止基準には特別な注意が必要です。

も参照してください
幅優先探索
深さ優先探索
任意の角度のパス計画、グラフのエッジに沿って移動するだけでなく、任意の角度をとることができるパスを検索します

ノート
^ 「A *のような」とは、A *と同様に、開始ノードから始まるパスを一度に1エッジずつ拡張することによってアルゴリズムが検索することを意味します。これには、たとえば、ゴールから後方に、または両方向に同時に検索するアルゴリズムは含まれません。さらに、この定理の対象となるアルゴリズムは、A *よりも許容可能であり、「十分な情報がない」必要が ^ f値が低い他のノードが残っている場合、ゴールへのパスが短くなる可能性があるため、ゴールノードは複数回渡される可能性が

参考文献
^ Russell、Stuart J.（2018）。人工知能は現代的なアプローチです。ノーヴィグ、ピーター（第4版）。ボストン：ピアソン。ISBN 978-0134610993。OCLC  1021874142。
^ デリング、D。; サンダース、P。; Schultes、D。; ワーグナー、D。（2009）。「エンジニアリングルート計画アルゴリズム」。大規模で複雑なネットワークのアルゴリズム：設計、分析、およびシミュレーション。コンピュータサイエンスの講義ノート。5515。スプリンガー。pp。11μ$ 7–139。CiteSeerX 10.1.1.164.8916。土井：10.1007 / 978-3-642-02094-0_7。ISBN
  978-3-642-02093-3。
^ Zeng、W。; チャーチ、RL（2009）。「実際の道路網で最短経路を見つける：A *の場合」。地理情報科学の国際ジャーナル。23（4）：531–543。土井：10.1080 / 13658810801949850。S2CID 14833639。
^ ハート、PE; ニルソン、NJ; ラファエル、B。（1968）。「最小コストパスのヒューリスティック決定の正式な基礎」。システム科学とサイバネティックスに関するIEEEトランザクション。4（2）：100–107。土井：10.1109 /TSSC.1968.300136。
^ ドラン、JE; Michie、D。（1966-09-20）。「グラフトラバーサープログラムを使用した実験」。手順 R.Soc。ロンド。A。294（1437）：235–259。Bibcode：1966RSPSA.294..235D。土井：10.1098 /rspa.1966.0205。ISSN 0080から4630まで。S2CID 21698093。
  
^ Nilsson、Nils J.（2009-10-30）。人工知能の探求（PDF）。ケンブリッジ：ケンブリッジ大学出版局。ISBN  9780521122931。
^ Edelkamp、Stefan; ジャバー、シャヒド; Lluch-Lafuente、Alberto（2005）。「コスト代数ヒューリスティック検索」（PDF）。人工知能に関する第20回全国会議（AAAI）の議事録：1362–1367。
^ ハート、ピーターE。; ニルソン、ニルスJ。; ラファエル、バートラム（1972-12-01）。「「最小コストパスのヒューリスティック決定の正式な根拠」への修正」（PDF）。ACM SIGART Bulletin（37）：28–29。土井：10.1145 /1056777.1056779。ISSN 0163から5719まで。S2CID 6386648。   
^ chter、Rina; ジューディアパール（1985）。「一般化された最良優先探索戦略とA *の最適性」。ACMのジャーナル。32（3）：505–536。土井：10.1145 /3828.3830。S2CID 2092415。
^ Smith、Michael John; グッドチャイルド、マイケルF。; Longley、Paul（2007）、Geospatial Analysis：A Comprehensive Guide to Principles、Techniques and Software Tools、Troubadour Publishing Ltd、p。344、ISBN
 9781905886609。
^ Hetland、Magnus Lie（2010）、Python Algorithms：Mastering Basic Algorithms in the Python Language、Apress、p。214、ISBN
 9781430232377。
^ マルテッリ、アルベルト（1977）。「許容される検索アルゴリズムの複雑さについて」。人工知能。8（1）：1–13。土井：10.1016 / 0004-3702（77）90002-9。
^ ポール、イラ（1970）。「ヒューリスティック検索におけるエラーの影響に関する最初の結果」。マシンインテリジェンス。5：219–236。
^ パール、ジューディア（1984）。ヒューリスティック：コンピューターの問題解決のためのインテリジェントな検索戦略。アディソン-ウェスリー。ISBN
 978-0-201-05594-8。
^ ポール、イラ（1973年8月）。「ヒューリスティックな問題解決における（相対的な）大惨事、ヒューリスティックな能力、真の動的な重み付け、および計算上の問題の回避」（PDF）。人工知能に関する第3回国際合同会議（IJCAI-73）の議事録。3。米国カリフォルニア州。pp。11–17。
^ Köll、Andreas; ヘルマン・カインドル（1992年8月）。「動的重み付けへの新しいアプローチ」。人工知能に関する第10回欧州会議（ECAI-92）の議事録。ウィーン、オーストリア。pp。16–17。
^ パール、ジューディア; ジン・H・キム（1982）。「半許容ヒューリスティックスの研究」。パターン分析とマシンインテリジェンスに関するIEEEトランザクション。4（4）：392–399。土井：10.1109 /TPAMI.1982.4767270。PMID 21869053。S2CID 3176931。
  
^ Ghallab、Malik; デニスアラード（1983年8月）。「ε -効率的に近い許容ヒューリスティック検索アルゴリズム」（PDF） 。人工知能に関する第8回国際合同会議（IJCAI-83）の議事録。2。カールスルーエ、ドイツ。pp。789–791。2014年8月6日にオリジナル（PDF）からアーカイブされました。
^ リース、ビョルン（1999）。「AlphA *：ε許容ヒューリスティック検索アルゴリズム」。
^ ラッセル、スチュアート; Norvig、Peter（2003）。人工知能：現代的なアプローチ（第2版）。プレンティスホール。pp。97–104。ISBN
 978-0137903955。
^ ラッセル、スチュアート; Norvig、Peter（2009）。人工知能：現代的なアプローチ（第3版）。プレンティスホール。NS。103. ISBN
 978-0-13-604259-4。
^ ラッセル、スチュアートJ.（2018）。人工知能は現代的なアプローチです。ノーヴィグ、ピーター（第4版）。ボストン：ピアソン。ISBN
 978-0134610993。OCLC  1021874142。
^ クライン、ダン; マニング、クリストファーD.（2003）。A *解析：高速で正確なビタビ解析選択。手順 NAACL-HLT。
^ Kagan E。; ベンガルI.（2014）。「オンライン情報学習によるグループテストアルゴリズム」（PDF）。IIEトランザクション。46（2）：164–184。土井：10.1080 /0740817X.2013.803639。
^ ファーガソン、デイブ; リカチェフ、マキシム; ステンツ、アンソニー（2005）。ヒューリスティックベースのパスプランニングガイド（PDF）。手順 自律システムの不確実性の下での計画に関するICAPSワークショップ。
^ ナウ、ダナS。; クマール、ヴィピン; カナル、ラビーン（1984）。「一般的な分枝限定法とそのA ∗およびAO ∗との関係」（PDF）。人工知能。23（1）：29–58。土井：10.1016 / 0004-3702（84）90004-3。
^ Hansen、Eric A.、およびRongZhou。「いつでもヒューリスティック検索。 ウェイバックマシンで2016年11月5日にアーカイブ」J.Artif。Intell。Res。（JAIR）28（2007）：267-297
^ https：//www.cambridge.org/core/journals/robotica/article/abs/investigating-reduced-path-planning-strategy-for-differential-wheeled-mobile-robot/6EDFFC11CEF00D0E010C0D149FE9C811。
^ Pijls、Wim; 投稿、ヘンク「最短経路のためのさらに別の双方向アルゴリズム」 Econometric Institute Report EI 2009-10 / Econometric Institute、エラスムス大学ロッテルダム。エラスムス経済大学院。
^ 「効率的なポイントツーポイント最短経路アルゴリズム」（PDF）。
プリンストン大学から

参考文献
ニルソン、NJ（1980）。人工知能の原則。カリフォルニア州パロアルト：Tioga Publishing Company ISBN 978-0-935382-01-3。

外部リンク
パスファインディングに関するアドバイスと考えを含む、明確な視覚的なA *説明
階層パスファインディングA *（HPA *）と呼ばれるA *のバリエーション
ブライアン・グリンステッド。「JavaScriptでのA *検索アルゴリズム（更新）」。”