ベジエ三角形

B%C3%A9zier_triangle
Aベジエ三角形の特別なタイプであるベジエ面（によって作成され、線形、二次、キュービックの制御点以上度）の補間。

コンテンツ
1 n次ベジエ三角形
2 キュービックベジエ三角形
2.1 立方体のベジエ三角形を半分にする
3 も参照してください
4 参考文献
5 外部リンク

n次ベジエ三角形
一般的なN番目の次ベジエ三角形を有する（N  + 1）（N  + 2）/ 2の制御点 α I β jのγ kはここで、I、  J、  kは非負である整数ようにI  +  J  +  K  =  N。次に、サーフェスは次のように定義されます。     （（ α +
β +γ u
）。 =∑ I+ + k = 私
、 、k ≥ 0（（NS I k ）。 I uk α I β γ
k= ∑ I+ + k = 私
、 、k ≥
0 ！ I ！ ！ k ！ I uk α I β γ k { displaystyle（ alpha s + beta t + gamma u）^ {n} = sum _ { begin {smallmatrix} i + j + k 、= 、n \ i、j、k 、 geq 、0 end {smallmatrix}} {n choice i j k} s ^ {i} t ^ {j} u ^ {k} alpha ^ {i} beta ^ {j} gamma ^ { k} = sum _ { begin {smallmatrix} i + j + k 、= 、n \ i、j、k 、 geq 、0 end {smallmatrix}} { frac {n！} {i！j！k！}} s ^ {i} t ^ {j} u ^ {k} alpha ^ {i} beta ^ {j} gamma ^ {k}}
  すべての非負の実数に対して s  +  t  +  u  = 1。
リニア（オーダー = 1 { textstyle n = 1}

 ）、結果のベジエ三角形は実際には通常の平らな三角形であり、三角形の頂点は3つの制御点に等しくなります。二次（ = 2 { textstyle n = 2}

 ）ベジェ三角形は、すべてエッジに配置された6つのコントロールポイントを備えています。キュービック（ = 3 { textstyle n = 3}

 ）ベジエ三角形は10個の制御点によって定義され、エッジに配置されていない内部制御点を持つ最低次のベジエ三角形です。すべての場合において、三角形のエッジは同じ次数のベジェ曲線になります。

キュービックベジエ三角形

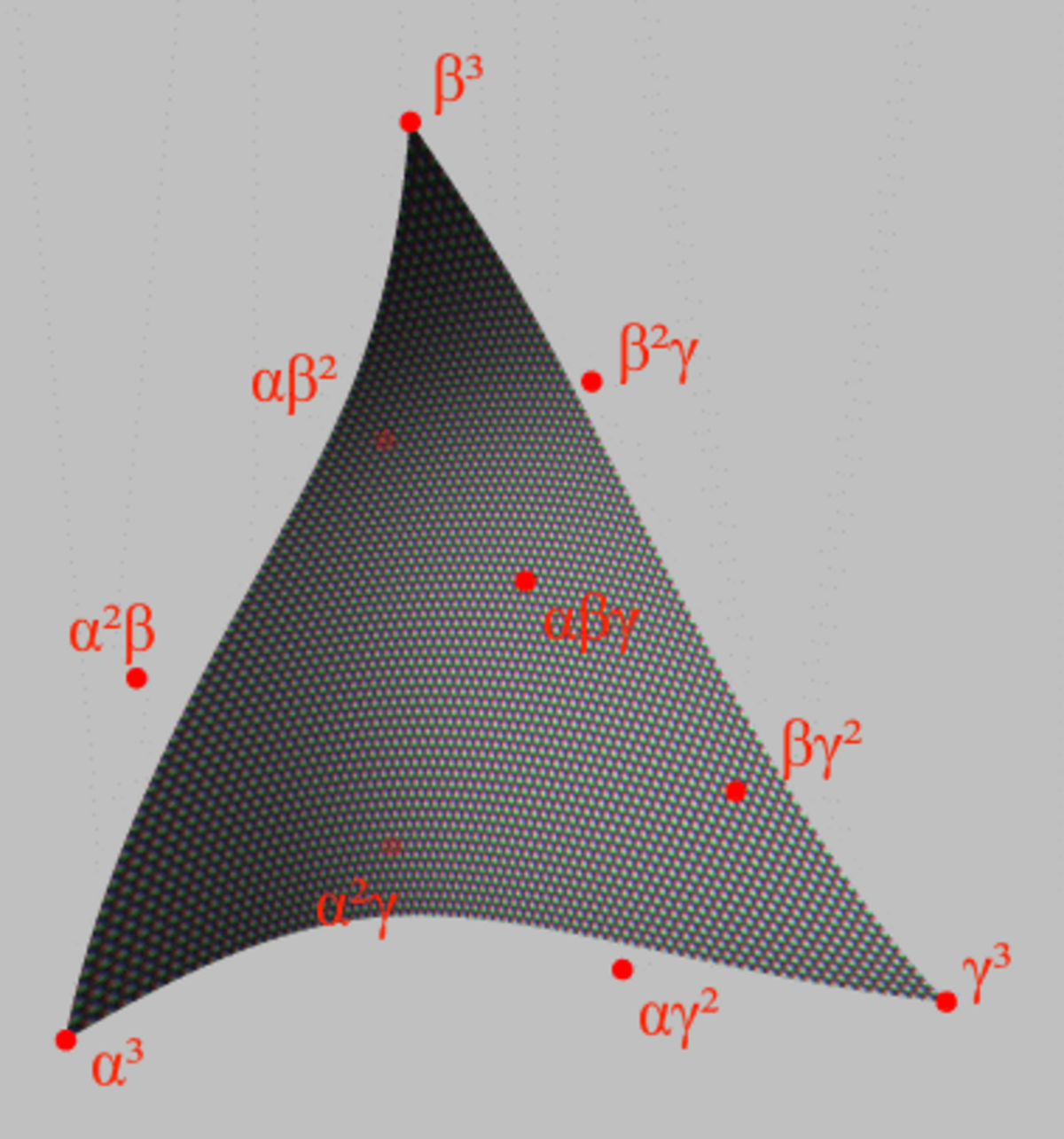
  制御点がマークされたベジェ三角形の例
立方ベジェ三角形である表面式 （（ 、 、 u ）。 = （（ α +
β + γ u
）。3 = β 3 3+3 2 2 +3 2
γ 2
u 3 2
β 2 +6
γ u+3 2 u 2 +
α 3 3 +3 2
γ 2 u +3 2 u 2 + γ 3 u 3 {{ begin {aligned} p（s、t、u）=（ alpha s + beta t + gamma u）^ {3} = ;＆ beta ^ {3} 、t ^ {3} +3 、 alpha beta ^ {2} 、st ^ {2} + 3 、 beta ^ {2} gamma 、t ^ {2} u ; + \＆3 、 alpha ^ {2} beta 、s ^ {2} t + 6 、 alpha beta gamma 、stu + 3 、 beta gamma ^ {2} 、tu ^ {2} 、+ \ ＆ alpha ^ {3} 、s ^ {3} + 3 、 alpha ^ {2} gamma 、s ^ {2} u + 3 、 alpha gamma ^ {2} 、su ^ {2} + gamma ^ {3} 、u ^ {3} end {aligned}}}
  ここで、α 3、β 3、γ 3、α 2 β、αβ 2、β 2 γ、βγ 2、αγ 2、α 2 γ及びαβγは三角形との制御点であるS、T、U 0≤と（S、t、u≤1およびs + t + u = 1）は、三角形の内側の重心座標です。
あるいは、3次ベジエ三角形は、次のように、より一般化された定式化として表すことができます。 （（ 、 、 u ）。= ∑ I+ +k I
、 、 k 0 （（ 3 I k ）。 I uk α I
β γk = ∑ I+ +k I
、 、
k 0 I ！ ！ k ！ I uk α I
β γ k {{ begin {aligned} p（s、t、u）＆= sum _ { begin {smallmatrix} i + j + k 、= 、3 \ i、j、k 、 geq 、0 end {smallmatrix}} {3 choice i j k} s ^ {i} t ^ {j} u ^ {k} alpha ^ {i} beta ^ {j} gamma ^ { k} = sum _ { begin {smallmatrix} i + j + k 、= 、3 \ i、j、k 、 geq 、0 end {smallmatrix}} { frac {6} { i！j！k！}} s ^ {i} t ^ {j} u ^ {k} alpha ^ {i} beta ^ {j} gamma ^ {k} end {aligned}}}
  処方に従って§ のn番目の次ベジエ三角形。
三角形の頂点は点αである3、β 3、γ 3。三角形のエッジはそれ自体がベジェ曲線であり、ベジエ三角形と同じ制御点が
γ除去することでUの期間、通常のベジェ曲線の結果を。また、物理的なコンピューター画面での表示にはあまり役立ちませんが、用語を追加すると、ベジエ四面体またはベジエポリトープが生成されます。
方程式の性質上、三角形全体が制御点で囲まれたボリューム内に含まれ、制御点のアフィン変換は同じ方法で三角形全体を正しく変換します。

立方体のベジエ三角形を半分にする
コンピュータグラフィックスにおけるベジエ三角形の利点は、ベジエ三角形を2つの別々のベジエ三角形に分割するために、浮動小数点演算ではなく、加算と2による除算のみが必要なことです。つまり、ベジエ三角形は滑らかですが、結果の三角形が十分に小さいと見なされるまで、三角形を2つに再帰的に分割することにより、正三角形を使用して簡単に近似できます。
以下を計算α角との完全なベジエ三角形の半分のための新たな制御点3、途中αとの間のベジエ曲線に沿って隅3およびβ 3、γ及び第三のコーナー3。（（ α
3′ α
2 β ′α β2′ β 3′ α
2 γ ′α β γ
′ β 2 γ ′α γ
2′ β γ
2′ γ
3 ′ ）。 = （（ 10 0 0 0 0 0 0 0 0 00 01 02 03
00 0 0 0 0 0 0 1 4 00 01 02 03
00 0 0 0 0 0 1 8 3 00 01 02 03
80 0 0 0 0 0 0 0 0 00 01 02 03
00 0 0 0 0 0 1 2 1 00 01 02 03
00 0 0 0 1 4 2 4 1 00 01 02 03
00 0 0 0 0 0 1 0 0 00 01 02 03
00 0 1 2 1 2 0 0 0 00 01 02 030 0 0 1
）。 ⋅ （（ α
3 α 2β α β
2 β 3 α 2γ α β γ β
2γ α γ
2β γ
2 γ 3 ）。 {{ begin {pmatrix} { boldsymbol { alpha ^ {3}}} {‘} \ { boldsymbol { alpha ^ {2} beta}} {‘} \ { boldsymbol { alpha beta ^ {2}}} {‘} \ { boldsymbol { beta ^ {3}}} {‘} \ { boldsymbol { alpha ^ {2} gamma}} {‘} \ { boldsymbol { alpha beta gamma}} {‘} \ { boldsymbol { beta ^ {2} gamma}} {‘} \ { boldsymbol { alpha gamma ^ {2}}} {‘} \ { boldsymbol { beta gamma ^ {2}}} {‘} \ { boldsymbol { gamma ^ {3}}} {‘} end {pmatrix}} = { begin { pmatrix} 1＆0＆0＆0＆0＆0＆0＆0＆0＆0 \ {1 over 2}＆{1 over 2}＆0＆0＆0＆0＆0＆0＆0＆0 \ {1 over 4}＆{2 over 4}＆{1 over 4}＆0＆0＆0＆0＆0＆0＆0 \ {1 over 8} ＆{3 over 8}＆{3 over 8}＆{1 over 8}＆0＆0＆0＆0＆0＆0 \ 0＆0＆0＆0＆1＆0＆0＆0＆0＆0 \ 0＆0＆0＆0＆{1 over 2}＆{1 over 2}＆0＆0＆0＆0 \ 0＆0＆0＆0＆{1 over 4 }＆{2 over 4}＆{1 over 4}＆0＆0＆0 \ 0＆0＆0＆0＆0＆0＆0＆1＆0＆0 \ 0＆0＆0＆0＆0＆0＆0＆{1 over 2}＆{1 over 2}＆0 \ 0＆0＆0＆0＆0＆0＆0＆0＆0＆1 end {pmatrix} {pmatrix} { boldsymbol { alpha ^ {3}}} \ { boldsymbol { alpha ^ {2} beta}} \ { boldsymbol { alpha beta ^ {2}}} \ { boldsymbol { beta ^ {3}}} \ { boldsymbol { alpha ^ {2} gamma}} \ { bolds ymbol { alpha beta gamma}} \ { boldsymbol { beta ^ {2} gamma}} \ { boldsymbol { alpha gamma ^ {2}}} \ { boldsymbol { beta gamma ^ {2}}} \ { boldsymbol { gamma ^ {3}}} end {pmatrix}}}
  同様に、加算と2による除算のみを使用して、 β 3 ：= （（ α β 2+ β 3 ）。/ 2 α β 2 ：=（（ α
2β + α β 2 ）。/ 2 β 3 ：=（（ α β 2+ β 3 ）。/ 2 α
2 β ：=（（ α
3+ α
2 β ）。
/2 β 2 ：= （（ α
2β + α β 2 ）。/ 2 β 3 ：=（（ α β 2+ β 3 ）。/ 2
{{ begin {matrix} && beta ^ {3}：=（ alpha beta ^ {2} + beta ^ {3}）/ 2 \＆ alpha beta ^ {2}：= （ alpha ^ {2} beta + alpha beta ^ {2}）/ 2＆ beta ^ {3}：=（ alpha beta ^ {2} + beta ^ {3}）/ 2 \ alpha ^ {2} beta：=（ alpha ^ {3} + alpha ^ {2} beta）/ 2＆ alpha beta ^ {2}：=（ alpha ^ {2} beta + alpha beta ^ {2}）/ 2＆ beta ^ {3}：=（ alpha beta ^ {2} + beta ^ {3}）/ 2 \ end {matrix}}}
β 2 γ ：=（（ αβ γ + β
2 γ ）。/ 2 α β γ ：= （（ α
2γ + α β γ
）。/ 2 β
2 γ ：=（（ αβ γ + β
2 γ ）。/ 2
{{ begin {matrix}＆ beta ^ {2} gamma：=（ alpha beta gamma + beta ^ {2} gamma）/ 2 \ alpha beta gamma：=（ alpha ^ {2} gamma + alpha beta gamma）/ 2＆ beta ^ {2} gamma：=（ alpha beta gamma + beta ^ {2} gamma）/ 2 \ end {matrix}}}
β γ 2 =（（ α
γ2 β γ
2）。/ 2
{ beta gamma ^ {2}：=（ alpha gamma ^ {2} + beta gamma ^ {2}）/ 2}

ここで、：=は、左側のベクトルを右側のベクトルに置き換えることを意味します。
ベジエ三角形を半分にすることは、ベジエ三角形の次数までのすべての次数のベジエ曲線を半分にすることに似ていることに注意して

も参照してください
ベジェ曲線
ベジエ曲面（双二次パッチはベジエ長方形です）
水面

参考文献
^ Farin、Gerald（2002）、コンピューター支援幾何学的設計の曲線と表面（5 ed。）、Academic Press Science＆Technology Books、ISBN 978-1-55860-737-8 ^ Postscriptでの3Dサーフェスレンダリング

外部リンク
描画プリミティブとしての2次ベジエ三角形平面および2次ベジエ三角形に関する詳細情報が含まれています。
レイトレーシングでのキュービックベジエパッチの使用に関する論文（ドイツ語）
「レイトレーシング三角形ベジェパッチ」。CiteSeerX  10.1.1.18.5646。 欠落または空|url=（ヘルプ）
「三角形のベジェクリッピング」。CiteSeerX  10.1.1.62.8062。 欠落または空|url=（ヘルプ）
湾曲したPN三角形（特殊な種類の3次ベジエ三角形）
多面体近似からの曲面シェーディングの形状認識法線補間
ピクセルシェーダーベースの湾曲した三角形
「三角形メッシュの頂点法線に基づく最小二乗加速度に近い表面構築」。CiteSeerX  10.1.1.6.2521。 欠落または空|url=（ヘルプ）”