カントール集合

Cantor_set

カントール空間
と混同しないでください 数学、カントール集合は単一である点の集合である線分直感的特性の数を有しています。1874年にヘンリージョンスティーブンスミスによって発見され 、1883年にドイツの数学者ゲオルクカントールによって導入されました。
このセットを検討することで、カントールと他の人々は、最新のポイントセットトポロジの基礎を築くのに役立ちました。カントール自身が一般的で抽象的な方法でセットを定義しましたが、最も一般的な現代の構造は、線分の中央3分の1を削除し、残りの短いセグメントでプロセスを繰り返すことによって構築されたカントール三元セットです。Cantor自身は、より一般的なアイデアの例として、どこにも密集していない完全集合の三項構造について言及しました。
カントール集合を​​拡大します。セット内の各ポイントは、ここでは垂直線で表されています。

コンテンツ
1 三項セットの構成と式
2 構成
3 プロパティ
3.1 カーディナリティ 3.2 自己相似性 3.3 保存則 3.43.4 トポロジー的および分析的特性 3.5 測定と確率 3.6 カンター番号 3.7 記述集合論
4 バリアント
4.1 スミス-ボルテラ-カントール集合 4.2 確率的カントール集合 4.3 カンターダスト
5 歴史的発言
6 も参照してください
7 ノート
8 参考文献
9 外部リンク

三項セットの構成と式
カントール三進集合 C { { mathcal {C}}}

 線分のセットから開いている中央の3分の1を繰り返し削除することによって作成されます。1つは、開いている中央の3分の1を削除することから始まります（（ 13 2 3 ）。 { textstyle left（{ frac {1} {3}}、{ frac {2} {3}} right）}

 間隔から
[ 0 1 ] { textstyle left }

 、2つの線分を残します：
[ 0 13 ] ∪ [ 2 3 1]
{ textstyle left [0、{ frac {1} {3}} right] cup left [{ frac {2} {3}}、1 right]}

 。次に、これらの残りの各セグメントの開いている中央の3分の1が削除され、4つの線分が残ります。
[ 0 19 ] ∪
[ 29 1 3 ] ∪
[ 23 7 9 ] ∪ [ 8 9 1]
{ textstyle left [0、{ frac {1} {9}} right] cup left [{ frac {2} {9}}、{ frac {1} {3}} right] cup left [{ frac {2} {3}}、{ frac {7} {9}} right] cup left [{ frac {8} {9}}、1 right]}

 。カントール3進集合には、区間内のすべての点が含まれます
[ 0 1 ] { }

 この無限のプロセスのどのステップでも削除されません。同じ事実を設定することで再帰的に記述できますC 0 ：= [ 0 1 ] { C_ {0}：= }

 と C n
：=C n
− ∪ （（ 23 C n
−1 3
）。 1 3（（ Cn − 1 ∪（（ 2 + Cn − 1 ）。 ）。 { C_ {n}：= { frac {C_ {n-1}} {3}} cup left（{ frac {2} {3}} + { frac {C_ {n-1} } {3}} right）= { frac {1} {3}} { bigl（} C_ {n-1} cup left（2 + C_ {n-1} right）{ bigr） }}
  にとってn ≥ 1
{ n geq 1}

 、 となることによって C ：=
{ { mathcal {C}}：=}

 ム n ∞ C n
{ { color {Blue} lim _ {n to infty} C_ {n}}}
= ⋂
n= 0 ∞
Cn = ⋂
n= m ∞
C n { = bigcap _ {n = 0} ^ { infty} C_ {n} = bigcap _ {n = m} ^ { infty} C_ {n}}

    任意の  m ≥ 0
{ m geq 0}

 。
このプロセスの最初の6つのステップを以下に示します。

自己相似変換のアイデアを使用して、
T L （（ X
）。=X / 3 T R （ X ）。 = （（ 2 +X ）。/ 3
{ T_ {L}（x）= x / 3、T_ {R}（x）=（2 + x）/ 3}

  と
Cn T L（（ Cn −
1）。∪ T R（（ Cn −
1）。 { C_ {n} = T_ {L}（C_ {n-1}） cup T_ {R}（C_ {n-1}）、}

 カントール集合の明示的な閉じた式はです。C =
[ 0 1] ∖ ⋃ = 0 ∞ =0 3 n 1 （（ 3 k +1 3n + 1 3 k+2 3n + 1
）。 { { mathcal {C}} = 、 setminus 、 bigcup _ {n = 0} ^ { infty} bigcup _ {k = 0} ^ {3 ^ {n} -1} left（{ frac {3k + 1} {3 ^ {n + 1}}}、{ frac {3k + 2} {3 ^ {n + 1}}} right）、}
  ここで、中央3分の1ごとが開区間として削除されます（（ 3 k +1 3n + 1 3 k+2 3n + 1 ）。 { textstyle left（{ frac {3k + 1} {3 ^ {n + 1}}}、{ frac {3k + 2} {3 ^ {n + 1}}} right）}

  閉区間から 3 k+0 3n + 1 3 k+3 3n + 1 ] = [ k +0 3 n k +1 3n ]
{ textstyle left [{ frac {3k + 0} {3 ^ {n + 1}}}、{ frac {3k + 3} {3 ^ {n + 1}}} right] = left [ { frac {k + 0} {3 ^ {n}}}、{ frac {k + 1} {3 ^ {n}}} right]}

  それを囲む、またはC = ⋂ = 1 ∞ =0 3 n − 1（（ [ 3 k +0 3n 3 k+1 3n ] ∪
[ 3 k +2 3n 3 k+3 3n ]
）。 { { mathcal {C}} = bigcap _ {n = 1} ^ { infty} bigcup _ {k = 0} ^ {3 ^ {n-1} -1} left（ left [ { frac {3k + 0} {3 ^ {n}}}、{ frac {3k + 1} {3 ^ {n}}} right] cup left [{ frac {3k + 2} { 3 ^ {n}}}、{ frac {3k + 3} {3 ^ {n}}} right] right）、}
  真ん中の3分の1（（ 3 k +1 3n 3 k+2 3 n ）。
{ textstyle left（{ frac {3k + 1} {3 ^ {n}}}、{ frac {3k + 2} {3 ^ {n}}} right）}

  前述の閉区間の [ k +0 3n − 1 k+1 3n − 1 ] =
[ 3 k +0 3n 3 k+3 3n ]
{ textstyle left [{ frac {k + 0} {3 ^ {n-1}}}、{ frac {k + 1} {3 ^ {n-1}}} right] = left [ { frac {3k + 0} {3 ^ {n}}}、{ frac {3k + 3} {3 ^ {n}}} right]}

  と交差することによって削除されます 3 k+0 3n 3 k+1 3n ] ∪
[ 3 k +2 3n 3 k+3 3 n ] { textstyle left [{ frac {3k + 0} {3 ^ {n}}}、{ frac {3k + 1} {3 ^ {n}}} right] cup left [{ frac {3k + 2} {3 ^ {n}}}、{ frac {3k + 3} {3 ^ {n}}} right]。}

中間の3分の1を削除するこのプロセスは、有限の細分割ルールの簡単な例です。カントール3進集合は、フラクタル文字列の例です。

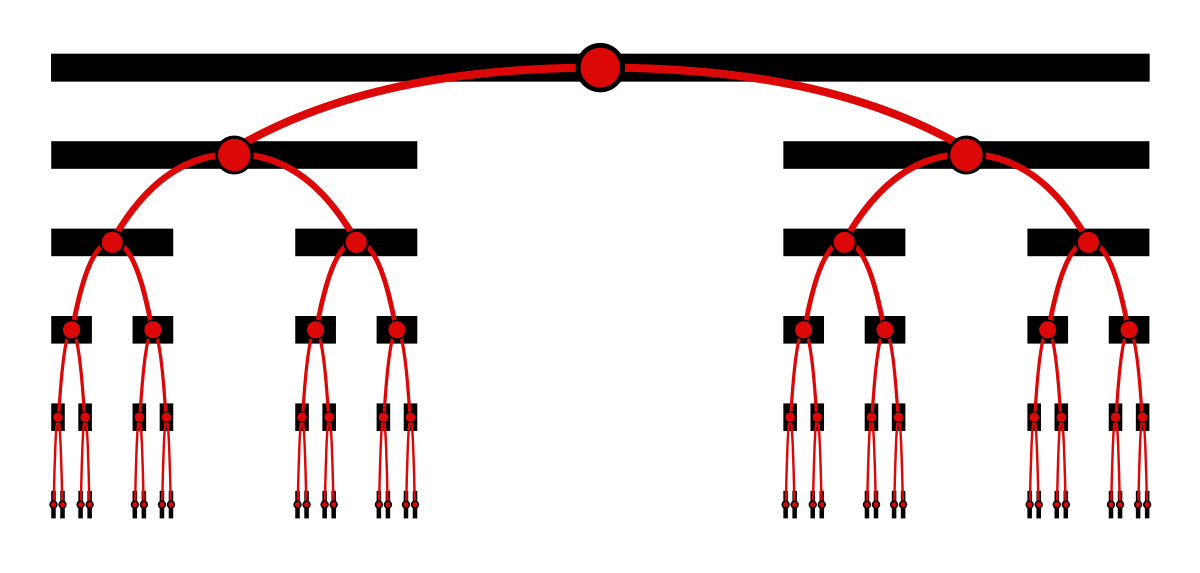
算術的には、カントール集合は単位区間のすべての実数で構成されます
[ 0 1 ] { }

 3進数（基数3）の分数として表現するために数字1を必要としないもの。上の図が示すように、カントール集合の各ポイントは、無限に深い二分木を通るパスによって一意に配置されます。パスは、削除されたセグメントのどちら側にあるかに従って、各レベルで左または右に曲がります。各左折を0で表し、各右折を2で表すと、ポイントの3項分数が得られます。

構成
カントール集合は除外されない点の集合として定義されるため、残りの単位区間の割合（つまり、メジャー）は、削除された全長によって求めることができます。この合計は等比数列です ∑ n= 0 ∞ 2 n 3 n+1 1 3 +2 9 +4 27+8 81+ ⋯ =1 3 （（ 1 1 −2 3
）。 = 1.1。
{ sum _ {n = 0} ^ { infty} { frac {2 ^ {n}} {3 ^ {n + 1}}} = { frac {1} {3}} + { frac {2} {9}} + { frac {4} {27}} + { frac {8} {81}} + cdots = { frac {1} {3}} left（{ frac {1} {1-{ frac {2} {3}}}} right）= 1。}
  残りの比率が1− 1 = 0になるようにします。
この計算は、カントール集合がゼロ以外の長さの区間を含むことができないことを示唆しています。何かが残っているのは意外に思われるかもしれません。結局のところ、削除された間隔の長さの合計は、元の間隔の長さに等しくなります。ただし、プロセスを詳しく見ると、各間隔の「中央3分の1」を削除するには、オープンセット（エンドポイントを含まないセット）を削除する必要があるため、何かが残っている必要があることがわかります。したがって、線分を削除します（1/3、
2/3）元の間隔からポイントを残します
1/3 と
2/3。削除される間隔は常に残りの間隔の内部にあるため、後続の手順ではこれら（または他の）エンドポイントは削除されません。したがって、カントール集合は空ではなく、実際には数え切れないほどの数の点が含まれています（無限の二分木のパスに関する上記の説明から次のように）。
建設セグメントの端点だけが残っているように見えるかもしれませんが、そうではありません。数字
1/4例えば、ユニークな三部形式0.020202 … = 0がある02。それは下3分の1、その3分の1の上3分の1、その上3分の1の下3分の1というように続きます。中央のセグメントの1つに含まれることはないため、削除されることはありません。ただし、1/3の累乗の倍数ではないため、中間セグメントのエンドポイントでもありません。セグメントのすべてのエンドポイントは、三項分数を終了しており、セットに含まれています
{{X ∈ [ 0 1] ∣ ∃ I ∈ N 0 X 3 ]0
∈Z }（（ ⊂N0 3 − N 0 ）。 { left {x in mid examples i in mathbb {N} _ {0}：x 、3 ^ {i} in mathbb {Z} right } qquad { Bigl（} subset mathbb {N} _ {0} 、3 ^ {- mathbb {N} _ {0}} { Bigr）}}
  これは可算無限集合です。したようカーディナリティ、ほぼすべてのカントール集合の要素は、間隔のエンドポイント、また1/4のような合理的なポイントではありません。カントール集合全体は実際には数えられません。

プロパティ

カーディナリティ
このプロセスには、最初から残っているポイントがいくつも残っているため、カントール集合は数えられないことを示すことができます。これを確認するために、カントール集合の関数fがあることを示します。 C { { mathcal {C}}}

 全射である閉区間に（すなわち、fマップから C { { mathcal {C}}}

 に）のカーディナリティが C { { mathcal {C}}}

 のそれ以上です。以来 C { { mathcal {C}}}

 はのサブセットであり、そのカーディナリティもそれ以上ではないため、Cantor–Bernstein–Schröderの定理により、2つのカーディナリティは実際には等しくなければなりません。
この関数を作成するには、基数3（または3進）表記で区間の点を考慮します。適切な三項分数、より正確には、次の要素を思い出して（（ Z ∖ {{0 }
）。 3− N 0 { { bigl（} mathbb {Z} setminus {0 } { bigr）} cdot 3 ^ {- mathbb {N} _ {0}}}

 、たとえば、この表記法で複数の表現を許可します
1/3、これは0.1 3 = 0.1 0 3と書くことができますが、0.0222 … 3 = 0.0 2 3、と
書くこともできます。2/3、それは0.2のように書くことができる3 = 0.2 0 3も0.1222 …として3 = 0.1 2 3。真ん中の3分の1を削除すると、これには0.1xxxxx … 3の形式の3進数の数字が含まれます。ここで、xxxxx … 3は厳密に00000 … 3から22222 … 3の間にしたがって、最初のステップの後に残っている数は、
0.0xxxxx … 3の形式の番号（0.022222 … 3 = 1/3を含む）
0.2xxxxx … 3の形式の番号（0.222222 … 3 = 1を含む）
これは、基数点の後の最初の桁が1ではないような3進表現の数値は、最初のステップの後に残っている数値であると言うことで要約できます。
2番目のステップでは、0.01xxxx … 3および0.21xxxx … 3の形式の数字を削除します。（エンドポイントに適切な注意を払って）残りの数字は、最初の数字のどちらも3進数ではないものであると結論付けることができます。2桁は1です。
このように続けると、ステップnで除外されない数は、n番目の桁が1ではない3進表現を持っている必要がカントール集合に含まれる数は、どのステップでも除外されてはなりません。完全に0と2で構成される数字表現を許可する必要が
1のような数字を強調する価値があります
1/3= 0.1 3及び
7/9= 0.21 3は、それらが0と2Sの完全なる三元符号有するように、カントール集合である：1 = 0.222を… 3 = 0 2 3、
1/3= 0.0222 … 3 = 0.0 2 3及び
7/9= 0.20222 … 3 = 0.20 2 3。すべての後者の数字は、「エンドポイント」であり、これらの実施例は正しい限界点の C { { mathcal {C}}}

 。同じことが左の限界点にも当てはまります C { { mathcal {C}}}

 、例えば
2/3= 0.1222 … 3 = 0.1 2 3 = 0.2 0 3及び
8/9= 0.21222 … 3 = 0.21 2 3 = 0.22 0 3。これらのエンドポイントはすべて、適切な三元 分数です（の要素Z ⋅ 3 − N 0 { mathbb {Z} cdot 3 ^ {- mathbb {N} _ {0}}}

 ）の形式
p/qここで、分数が既約分数の場合、分母qは3の累乗です。これらの分数の3進表現は終了します（つまり、有限です）。または、適切な3進分数にはそれぞれ2つの表現があることを上から思い出して無限であり、無限に多くの繰り返し0または無限に多くの繰り返し2で「終了」します。そのような分数はの左限界点です C { { mathcal {C}}}

 その3進表現に1が含まれておらず、無限に多くの繰り返し0で「終了」する場合。同様に、適切な三項分数は、 C { { mathcal {C}}}

  再びその3進展開に1が含まれず、無限に多くの繰り返し2で「終了」する場合。
エンドポイントのこのセットは、密で C { { mathcal {C}}}

 （ただし、では密ではありません）、可算無限集合を構成します。の数字 C { { mathcal {C}}}

 エンドポイントではないものも、3進表現に0と2しかありませんが、エンドポイントになるため、数字0または数字2の無限の繰り返しで終了することはできません。
からの機能 C { { mathcal {C}}}

 to は、完全に0と2で構成される3進数を取り、すべての2を1に置き換え、シーケンスを実数の2進表現として解釈することによって定義されます。式では、 f （（ ∑
k∈ N a k 3 − k
）。= ∑
k∈ N a k 2 − k
{ f { bigg（} sum _ {k in mathbb {N}} a_ {k} 3 ^ {-k} { bigg）} = sum _ {k in mathbb {N} } { frac {a_ {k}} {2}} 2 ^ {-k}}

    どこ  ∀ k ∈ N
：a k ∈
{{ 0 2 } { forall k in mathbb {N}：a_ {k} in {0，2 }。}
  任意の数のためにY で、そのバイナリ表現は、数値の三元表現に変換することができるXで C { { mathcal {C}}}

 すべての1を2に置き換えます。これとF（X）= yのようにYがである範囲のF。たとえば、y =
3/5= 0.100110011001 … 2 = 0の1001年、私たちは書くのx = 0。2002 = 0.200220022002 … 3 =
7/10。したがって、fは全射です。ただし、fは単射ではありません 。f（x）が一致する値は、削除された中央3分の1の一方の両端の値です。たとえば、
1/3= 0.0 2 3（これはの正しい限界点です C { { mathcal {C}}}

  中央3分の1の左限界点[ 1/3、
2/3]） と
2/3= 0.2 0 3（これはの左限界点です C { { mathcal {C}}}

  中央3分の1の右限界点[ 1/3、
2/3]）
それで f （（1 3
）。= f（（ 0.02 ¯ 3
）。= 0.0 1 ¯ 2 = 0.1 2 = =0 =1 =2 =3= f（（ 0.20 ¯ 3
）。= f（（2 3
）。 ∥ 2
{ { begin {array} {lcl} f { bigl（} {} ^ {1} ！！/ ！_ {3} { bigr）} = f（0.0 { overline {2} } _ {3}）= 0.0 { overline {1}} _ {2} = ！！＆！！0.1_ {2} ！！＆！！= 0.1 { overline {0 }} _ {2} = f（0.2 { overline {0}} _ {3}）= f { bigl（} {} ^ {2} ！！/ ！_ {3} { bigr） }。\＆ parallel \＆{} ^ {1} ！！/ ！_ {2} end {array}}}
  したがって、カントール集合には、区間（数え切れないほどのカーディナリティがあります）にあるのと同じ数のポイントがc = 2 ℵ 0
{ { mathfrak {c}} = 2 ^ { aleph _ {0}}}

 ）。ただし、削除された区間の端点のセットは可算であるため、カントール集合には区間の端点ではない数が数え切れないほど多く存在する必要が上記のように、そのような数の一例は次のとおりです。
1/4、これは、0.020202 …のように書くことができる3 = 0 02三元表記。実際、a ∈
[ −1 1 ]
{ a in }

 、 が存在しますX y∈ C
{ x、y in { mathcal {C}}}

  そのようなa = y −X
{ a = yx}

 。これは、1917年にスタインハウスによって最初に実証されました。スタインハウスは、幾何学的な議論を通じて、次のような同等の主張を証明しました。 {{ （（ X y
）。∈ R2 y =X + a } ∩（（ C ×× C）。≠ ∅
{ {（x、y） in mathbb {R} ^ {2} mid y = x + a } ; cap ;（{ mathcal {C}} times { mathcal { C}}） neq emptyset}

  すべてのためのa ∈
[ −1 1 ]
{ a in }

 。この構造はからの注入を提供するので
[ −1 1 ]
{ }

  にC × C
{ { mathcal {C}} times { mathcal {C}}}

 、 我々は持っています
|C × C | ≥ |
[ −1 1 ] | = c
{ | { mathcal {C}} times { mathcal {C}} | geq | | = { mathfrak {c}}}

 即時の結果として。仮定して| A
××A | = | A |
{ | A times A | = | A |}

  無限集合の場合 A { A}

 （と同等であることが示さ声明選択公理によってタルスキー）、これはという別のデモを提供します| C | = c
{ | { mathcal {C}} | = { mathfrak {c}}}

 。
カントール集合には、それが取得された間隔と同じ数の点が含まれていますが、それ自体にはゼロ以外の長さの間隔は含まれ無理数は同じ性質を持っていますが、カントール集合には閉じられるという追加の性質があるので、すべての区間で密である無理数とは異なり、どの区間でも密ではありません。
すべての代数的無理数は正常であると推測されています。カントール集合のメンバーは正常ではないため、これは、カントール集合のすべてのメンバーが有理数または超越数のいずれかであることを意味します。

自己相似性
カントール集合はフラクタルのプロトタイプです。それは自己相似各コピーは3倍に縮小し、翻訳される場合には、自身の2枚のコピーに等しいので、。より正確には、カントール集合は、それ自体の左右の自己相似変換という2つの関数の和集合に等しくなります。T L （ X ）。=X / 3
{ T_ {L}（x）= x / 3}

  と
T R （（ X
）。 = （（ 2 +X ）。/ 3
{ T_ {R}（x）=（2 + x）/ 3}

 、カントール集合を同相写像まで不変のままにします：T L（（ C）。≅ T R（（ C）。≅ C =T L （（ C）。∪ T R（（ C）。 { T_ {L}（{ mathcal {C}}） cong T_ {R}（{ mathcal {C}}） cong { mathcal {C}} = T_ {L}（{ mathcal { C}}） cup T_ {R}（{ mathcal {C}}）。}

繰り返される反復のT L
{ T_ {L}}

  と
T R { T_ {R}}

 無限の二分木として視覚化することができます。つまり、ツリーの各ノードで、左側または右側のサブツリーを検討できます。セットを取る
{{T L T R } { {T_ {L}、T_ {R} }}

 関数の合成とともに、モノイド、ダイアディックモノイドを形成します。
二分木の自己同型はその双曲線回転であり、モジュラー群によって与えられます。したがって、カントール集合は、任意の2点に対して等質空間です。X
{ x}

  と y { y}

  カントール集合 C { { mathcal {C}}}

 、同相写像が存在するh ： C C
{ h：{ mathcal {C}} to { mathcal {C}}}

  と h （（ X
）。= y
{ h（x）= y}

 。の明示的な構成 h { h}

 カントール集合を離散空間の可算数のコピーの積空間として見ると、より簡単に説明できます。
{{0 1 }
{ {0，1 }}

 。次に地図h ：
{{0 1 } N
{{0 1 } N
{ h： {0，1 } ^ { mathbb {N}} to {0，1 } ^ { mathbb {N}}}

  によって定義されます
h n （（ u ）。 ：=u n X n +y n モッド 2 { h_ {n}（u）：= u_ {n} + x_ {n} + y_ {n} mod 2}

  交換する対合同相写像ですX
{ x}

  と y { y}

 。

保存則
スケーリングと自己相似性の背後には、何らかの形の保存則が常に責任があることがわかっています。カントール集合の場合、d f
{ d_ {f}}

 この瞬間（ここで
d f = ln （（ 2
）。/ ln （ 3 ）。
{ d_ {f} = ln（2）/ ln（3）}

 はフラクタル次元です）、構築プロセスの任意の段階で存続するすべての間隔は、カントール集合の場合は1に等しい定数に等しくなります。 あることを私たちは知っていますN = 2 n
{ N = 2 ^ {n}}

  サイズの間隔1 /
3 n { 1/3 ^ {n}}

  システムに存在する n { n}

 その建設の第3段階。次に、存続する間隔に次のようにラベルを付けます。X 1 X 2 … X2
{ x_ {1}、x_ {2}、 ldots、x_ {2 ^ {n}}}

  そうして
d f { d_ {f}}

 この瞬間は 1 d f+X 2 d
f+ ⋯+X2 d f= 1
{ x_ {1} ^ {d_ {f}} + x_ {2} ^ {d_ {f}} + cdots + x_ {2 ^ {n}} ^ {d_ {f}} = 1}

  以来 1X2 ⋯=X2 = 1 /
3 n { x_ {1} = x_ {2} = cdots = x_ {2 ^ {n}} = 1/3 ^ {n}}

 。
カントール集合のハウスドルフ次元は、ln（2）/ ln（3）≈0.631に等しくなります。

トポロジー的および分析的特性
「the」カントール集合は通常、上記の元の3分の1のカントールを指しますが、トポロジー学者はしばしば「a」カントール集合について話します。これは、同相写像（トポロジー的に同等）の位相空間を意味します。
上記の総和引数が示すように、カントール集合は非可算ですが、ルベーグ測度は0です。カントール集合は開いた集合の和集合の補数であるため、それ自体が実数の閉じたサブセットであり、したがって完全なメトリック空間です。全有界空間でもあるため、ハイネ・ボレルの定理はコンパクトでなければならないと言っています。
カントール集合内の任意の点およびその点の任意の小さな近傍には、3進数が0と2のみのその他の数値、および3進数に1が含まれる数値がしたがって、カントール集合のすべての点は、カントール集合の累積点（クラスター点または限界点とも呼ばれます）ですが、内部点はありません。すべてのポイントが蓄積ポイントとも呼ばれされている閉集合完璧なセットでトポロジなしインテリアのポイントとの間隔の閉じたサブセットであるが、どこにも密な間隔インチ
カントール集合のすべての点は、カントール集合の補集合の累積点でも
カントール集合の任意の2つのポイントについて、それらが異なる3進数が1つは0で、もう1つは2です。この数字の値に応じてカントール集合を​​「半分」に分割することにより、1つは次のパーティションを取得します。カントール集合は、元の2つの点を分離する2つの閉じた集合になります。カントール集合の相対トポロジーでは、点は開かつ閉集合で区切られています。その結果、カントール集合は完全に切断されます。コンパクトな完全不連結ハウスドルフ空間として、カントール集合はストーン空間の一例です。
位相空間、カントール集合は当然である同相に、製品の可算多くのスペースのコピー
{{0 1 }
{ {0，1 }}

 、ここで、各コピーは個別のトポロジを運びます。これは、2桁のすべてのシーケンスのスペースです2 N = {{ （（ X n ）。∣X n ∈
{{0 1 }
 にとって 
n∈ N
} { 2 ^ { mathbb {N}} = {（x_ {n}） mid x_ {n} in {0，1 } { text {for}} n in mathbb {N } }、}
  これは、2アディック整数のセットでも識別できます。製品トポロジーのオープンセットの基礎はシリンダーセットです。同相写像は、カントール集合が実数直線上の自然なトポロジーから継承する部分空間トポロジーにこれらをマッピングします。コンパクト空間の積としてのカントール空間のこの特徴付けは、チコノフの定理を介して、カントール空間がコンパクトであることの2番目の証拠を与えます。
上記の特性から、カントール集合はp進数の整数に同相であり、1つの点が削除されている場合は、p進数の数に同相です。
カントール集合は実数のサブセットであり、通常の距離計量に対する距離空間です。したがって、カントール集合自体は、同じ距離を使用することにより、距離空間になります。または、p進メトリックを使用することもできます。2 N
{ 2 ^ { mathbb {N}}}

 ：与えられた2つのシーケンス（（ X
n）。 （（ y
n）。∈ 2 N
{（x_ {n}）、（y_ {n}） in 2 ^ { mathbb {N}}}

 、それらの間の距離は d （（ （（ X
n）。 （（ y
n）。
）。= 2 − k { d（（x_ {n}）、（y_ {n}））= 2 ^ {-k}}

 、 どこ k { k}

  次のような最小のインデックスです
Xk y k
{ x_ {k} neq y_ {k}}

 ; そのようなインデックスがない場合、2つのシーケンスは同じであり、1つは距離をゼロと定義します。これらの2つのメトリックは、カントール集合で同じトポロジーを生成します。
カントール集合は完全に切り離された完全コンパクト距離空間であることを上で見てきました。確かに、ある意味ではそれが唯一のものです。空でない完全に切断された完全コンパクト距離空間はすべて、カントール集合と同相です。カントール集合に同相の空間の詳細については、カントール空間を参照して
カントール集合は、コンパクト距離空間のカテゴリでは「ユニバーサル」と見なされることがこれは、コンパクト距離空間がカントール集合の連続画像であるためです。ただし、この構造は一意ではないため、カントール集合は正確なカテゴリの意味で普遍的ではありません。「普遍的」特性は、関数解析において重要な用途があり、コンパクトな距離空間の表現定理として知られることも
任意の整数のためのQ ≥2、グループG =でトポロジーZ Q ω（可算直接和）が離散的です。がPontrjaginデュアルΓもあるZのq ω、Γのトポロジーはコンパクトです。Γは完全に切断されており、完全であることがわかります。したがって、カントール集合と同相です。q = 2の場合、同相写像を明示的に書き出すのが最も簡単です。（Rudin 1962 p 40を参照して）
カントール集合の幾何平均は約0.274974です。

測定と確率
カントール集合は、バイナリシーケンスのコンパクトグループと見なすことができるため、自然なハール測度が与えられます。セットの測度が1になるように正規化すると、コイン投げの無限シーケンスのモデルになります。さらに、区間の通常のルベーグ測度はカントール集合のハール測度の画像であり、三元集合への自然注入は特異測度の標準的な例であることを示すことができます。ハール測度が任意の確率のイメージであることも示すことができ、カントールはいくつかの方法で普遍的な確率空間を設定します。
ルベーグ測度理論、カントール集合は無数であり、ゼロ指標を有する一連の一例です。

カンター番号
カントール集合のメンバーとしてカントール数を定義すると、
のすべての実数は、2つのCantor数の合計です。
任意の2つのCantor番号の間に、Cantor番号ではない番号が

記述集合論
カントール集合は、のサブセットとしてのわずかなセット（または最初のカテゴリのセット）です（ただし、ベール空間であるため、それ自体のサブセットとしてではありません）。したがって、カントール集合は、カーディナリティ、メジャー、および（ベール）カテゴリの観点からの「サイズ」の概念が一致する必要がないことを示しています。セットのようにQ ∩
[ 0 1 ] { mathbb {Q} cap }

 、カントール集合 C { { mathcal {C}}}

 はヌルセット（メジャーゼロのセット）であり、のわずかなサブセットであるという意味で「小さい」です。ただし、Q ∩
[ 0 1 ] { mathbb {Q} cap }

 、可算で「小さな」カーディナリティを持っている、 0
{ aleph _ {0}}

 、のカーディナリティ C { { mathcal {C}}}

  連続体であると同じです c { { mathfrak {c}}}

 、およびカーディナリティの意味で「大きい」です。実際、のサブセットを構築することも可能です。これは、わずかであるが正のメジャーであり、サブセットは、わずかではないがメジャーがゼロです。「太い」カントールの可算和集合を取ることによって。セット C （（ n ）。 { { mathcal {C}} ^ {（n）}}

  メジャーのλ =（（ n− 1
）。/ n
{ lambda =（n-1）/ n}

  （構造については、以下のSmith–Volterra–Cantorセットを参照してください）、セットを取得しますA = ⋃ n = 1 ∞ C（（ n ）。 { textstyle { mathcal {A}}：= bigcup _ {n = 1} ^ { infty} { mathcal {C}} ^ {（n）}}

 これは正の測度（1に等しい）を持ちますが、ではわずかです。 C （（ n ）。 { { mathcal {C}} ^ {（n）}}

 どこにも密ではありません。次に、セットを検討しますA c =
[ 0 1] ∖ ⋃ n = 1 ∞ C（（ n ）。 { textstyle { mathcal {A}} ^ { mathrm {c}} = setminus bigcup _ {n = 1} ^ { infty} { mathcal {C}} ^ {（n ）}}

 。以来 A ∪A c =
[ 0 1 ] { { mathcal {A}} cup { mathcal {A}} ^ { mathrm {c}} = }

 、A c
{ { mathcal {A}} ^ { mathrm {c}}}

  貧弱になることはできませんが、 μ （（ A）。= 1
{ mu（{ mathcal {A}}）= 1}

 、A c
{ { mathcal {A}} ^ { mathrm {c}}}

  メジャーゼロが必要です。

バリアント

スミス-ボルテラ-カントール集合
Smith–Volterra–Cantorセット
カントール集合のようにすべてのピースの中央3分の1を繰り返し削除する代わりに、中央から他の固定パーセンテージ（0％と100％以外）を削除し続けることもできます。真ん中の場合
8/10間隔の一部が削除されると、非常にアクセスしやすいケースが得られます。セットはのすべての数値で構成され、完全に0と9で構成される小数として記述できます。各段階で一定のパーセンテージが削除されると、残りの長さがゼロになるため、制限セットの測定値はゼロになります。（（ 1− f
）。n 0
{（1-f）^ {n} to 0}

  なのでn ∞
{ n to infty}

 そのような任意のfのために0 < f ≤ 1
{ 0
 。
一方、ポジティブメジャーの「ファットカントール集合」は、各反復でセグメントの中央の小さな部分を削除することによって生成できます。したがって、どこにも密ではないが、正のルベーグ測度を持つカントール集合に同相写像を構築することができます。長さの間隔の場合r n
{ r ^ {n}}

  （（ r≤ 1 / 3
{ r leq 1/3}

 ）はn回目の反復で各セグメントの中央から削除され、削除された全長は次のようになります。∑ n = 1 ∞ 2 n − 1r n =r /（（ 1− 2 r ）。 { textstyle sum _ {n = 1} ^ { infty} 2 ^ {n-1} r ^ {n} = r /（1-2r）}

 、および極限集合には、ルベーグ測度がλ =（（ 1− 3 r
）。 / （（ 1− 2 r ）。 { lambda =（1-3r）/（1-2r）}

 。したがって、ある意味で、カントール集合の3分の1は、r = 1 / 3
{ r = 1/4}

 。もしも0 < r < 1 / 3
{ 0
 、その後、残りの部分は正の測度を持ちます0 < λ < 1
{ 0 < lambda <1}

 。ケースr = 1 / 4
{ r = 1/4}

 スミス-ボルテラ-カントール集合として知られています。これは、ルベーグ測度が1 / 2
{ 1/2}

 。

確率的カントール集合
カントール集合の構成は、均等にではなくランダムに分割することで変更できます。さらに、時間を組み込むために、使用可能なすべての間隔を分割するのではなく、各ステップで使用可能な間隔の1つだけを分割できます。確率的三項カントール集合の場合、結果として生じるプロセスは次の反応速度式で記述できます ∂ c（（ X t ）。 ∂t =
−X2 c （（ X t
）。+ 2 ∫
X ∞ （（ y −X ）。 c （（ y t
）。 d y { { frac { partial c（x、t）} { partial t}} =-{ frac {x ^ {2}} {2}} c（x、t）+2 int _ { x} ^ { infty}（yx）c（y、t）、dy、}
  確率的二項カントール集合∂ c（（ X t ）。 ∂t = −X c（（ X t
）。 + （（ 1+ p
）。 ∫ X∞ c（（ y t
）。 d y { {{ partial c（x、t）} over { partial t}} = -xc（x、t）+（1 + p） int _ {x} ^ { infty} c（y 、t）、dy、}
  どこ c （（ X t
）。 dX { c（x、t）dx}

  間のサイズの間隔の数ですX
{ x}

  とX+ dX
{ x + dx}

 。トライアドカントール集合の場合、フラクタル次元は 0.5616 { 0.5616}

  これは決定論的な対応物よりも少ないです 0.6309 { 0.6309}

 。確率的二項カントール集合の場合、フラクタル次元は p { p}

  これもまた、決定論的な対応物よりも少ないです ln （（ 1+ p
）。/ ln 2 { ln（1 + p）/ ln 2}

 。確率的二項カントールの場合、 c （（ X t ）。 { c（x、t）}

 長時間の制限でのソリューションとして動的スケーリングを示しますt −（（ 1+ d f ）。e −
X t { t ^ {-（1 + d_ {f}）} e ^ {-xt}}

  ここで、確率的二項カントール集合のフラクタル次元
d f = p { d_ {f} = p}

 。どちらの場合でも、トライアドカントール集合のように、d f
{ d_ {f}}

 この瞬間（ ∫X d f c （（ X t
）。dX =
絶え間ない
{ textstyle int x ^ {d_ {f}} c（x、t）、dx = { text {constant}}}

 ）確率的三項および二項カントール集合も保存量です。

カンターダスト
カントールダストは、カントール集合の多次元バージョンです。カントール集合の有限デカルト積をカントール空間にすることで形成できます。カントール集合と同様に、カントールダストの測定値はゼロです。

  カントールの立方体がカントールの塵に向かって再帰的に進行する

カンターダスト（2D）

カンターダスト（3D）
カントール集合の別の2Dアナログは、シェルピンスキーのカーペットです。このカーペットでは、正方形が9つの小さな正方形に分割され、中央の正方形が削除されています。その後、残りの正方形はさらにそれぞれ9つに分割され、中央が削除され、以下同様に無限に続きます。これの3Dアナログの1つは、メンガースポンジです。

歴史的発言

  カントール集合を​​連想させるパターンを持つ柱頭ですが、3項ではなく2進数で表されます。イル=ドフィラエの彫刻
説明ドールエジプトジーン・バプティスト・プロスパー・ジョロイスとエドゥアール・Devilliers、IMPRIMERIEインペリアーレ、パリ、1809年から1828年によって
Cantor自身がセットを一般的で抽象的な方法で定義し、より一般的なアイデアの例として、どこにも密集していない完全集合の三項構造について言及しました。元の論文は、抽象的な概念のいくつかの異なる構造を提供します。
このセットは、Cantorが考案した時点では抽象的であると見なされていたでしょう。Cantor自身は、三角級数が収束しない可能性のある一連の点に関する実際的な懸念によってそれに導かれました。この発見は、彼を無限集合の抽象的な一般理論を開発するための道に導くのに大いに役立ちました。

も参照してください
カントール集合のインジケーター機能
スミス-ボルテラ-カントール集合
六十四卦（易経）
カントール関数
カントールの立方体
アントワーヌの首輪
コッホスノーフレーク
ナスタークラトフスキファン
ハウスドルフ次元によるフラクタルのリスト
モーザー-ドゥブランシーケンス

ノート
^ スミス、ヘンリーJS（1874）。「不連続関数の統合について」。ロンドン数学会の議事録。最初のシリーズ。6：140〜153。
^ 「カントール集合」は、 Paul du Bois-Reymond（1831–1889）によっても発見されました。参照 デュ・ボワレイモン、ポール（1880年）、””Integralrechnungデア・デアBeweisデFundamentalsatzes”” 、Mathematische Annalen（ドイツ語）、16、P上の脚注。128。「カントール集合」は、1881年にVito Volterra（1860–1940）によっても発見されました。参照：
Volterra、Vito（1881）、 “”Alcune osservazioni sulle funzioni punteggiate discontinue”” [点ごとの不連続関数に関するいくつかの観察]、Giornale di Matematiche（イタリア語）、19：76–86。
^ Ferreirós、José（1999）。思考の迷宮：集合論の歴史と現代数学におけるその役割。スイス、バーゼル：BirkhäuserVerlag。頁 162 -165。ISBN
 9783034850513。
^ スチュワート、イアン（1997年6月26日）。神はダイスを演じますか？：カオスの新しい数学。ペンギン。ISBN
 0140256024。
^ カントール、ゲオルク（1883）。「Überunendliche、lineare Punktmannigfaltigkeiten V」 [無限の線形点多様体（セット）、パート5]。Mathematische Annalen（ドイツ語）。21：545–591。土井：10.1007 / bf01446819。S2CID 121930608。
^ Peitgen、H.-O。; ユルゲンス、H。; Saupe、D。（2004）。カオスとフラクタル：科学の新しいフロンティア（第2版）。NY、NY：SpringerVerlag。p。 65。ISBN
 978-1-4684-9396-2。
^ Soltanifar、Mohsen（2006）。「ミドルファミリーの異なる記述-カントール集合」。学部研究のアメリカジャーナル。5（2）：9–12。土井：10.33697 /ajur.2006.014。
^ Belcastro、Sarah-Marie; グリーン、マイケル、「カントール集合には1 4
{ { tfrac {1} {4}}}

 ？本当に？」、The College Mathematics Journal、32（1）：55、doi：10.2307 / 2687224、JSTOR  2687224
^ 終端符号付き数のこの代替繰り返し表示は任意で発生位置システムとアルキメデスの絶対値。
^ Carothers、NL（2000）。実解析。ケンブリッジ：ケンブリッジ大学出版局。頁。  31 -32。ISBN
 978-0-521-69624-1。
^ Krapivsky、PL; ベンナイム、E。（1994）。「確率的フラクタルにおけるマルチスケーリング」。物理文字A。196（3-4）：168 Bibcode：1994PhLA..196..168K。土井：10.1016 / 0375-9601（94）91220-3。
^ Hassan、MK; ロジャース、GJ（1995）。「断片化と確率的フラクタルのモデル」。物理文字A。95（1）：208 Bibcode：1995PhLA..208 … 95H。土井：10.1016 / 0375-9601（95）00727-K。
^ ウィラード、スティーブン（1968）。一般的なトポロジ。アディソン-ウェスリー。ASIN B0000EG7Q0。
^ カントール集合の幾何平均
^ アーバイン、ローラ。「定理36：カントール集合はゼロ測度の非可算集合です」。今週の定理。
^ Schroeder、Manfred（1991）。フラクタル、カオス、べき法則：無限の楽園から数分。ドーバー。pp。164–165。ISBN
 0486472043。
^ Gelbaum、Bernard R.（1964）。分析における反例。Olmsted、John MH（John Meigs Hubbell）、1911-1997。サンフランシスコ：Holden-Day。ISBN
 0486428753。OCLC  527671。
^ ハッサン、MK; パベル、NI; パンディット、RK; クルツ、J。（2014）。「ダイアディックカントール集合とその速度論的および確率論的対応物」。カオス、ソリトン、フラクタル。60：31–39。arXiv：1401.0249。Bibcode：2014CSF …. 60 … 31H。土井：10.1016 /j.chaos.2013.12.010。S2CID 14494072。
^ Helmberg、Gilbert（2007）。フラクタルに精通する。Walter de Gruyter p。46. ISBN
 978-3-11-019092-2。
^ Helmberg、Gilbert（2007）。フラクタルに精通する。Walter de Gruyter p。48. ISBN
 978-3-11-019092-2。

参考文献
スティーン、リン・アーサー; Seebach、J。Arthur Jr.（1995）。トポロジーの反例（1978年版のドーバー復刻版）。ベルリン、ニューヨーク：Springer-Verlag。実施例29 ISBN 978-0-486-68735-3。MR  0507446。
ワイズ、ゲイリーL。; ホール、エリックB.（1993）。確率と実解析の反例。ニューヨーク：オックスフォード大学出版局。第1章ISBN 0-19-507068-2。
ファルコナー、KJ（1986年7月24日）。フラクタル集合の幾何学。ケンブリッジ数学の道。ケンブリッジ大学出版局。ISBN 0521337054。
マティラ、ペルッティ（1999年2月25日）。ユークリッド空間における集合と測度の幾何学：フラクタルと修正可能性。ケンブリッジは高度な数学を研究しています。ケンブリッジ大学出版局。ISBN 0521655951。
マティラ、ペルッティ（2015）。フーリエ解析とハウスドルフ次元。ケンブリッジは高度な数学を研究しています。ケンブリッジ大学出版局。ISBN 9781316227619。。
ジグムンド、A。（1958）。三角級数、巻。IとII。ケンブリッジ大学出版局。

外部リンク
「カントール集合」、数学百科事典、EMS Press、2001年
カントール集合とカントールの設定や機能でカットノット
プラトニックレルムに設定されたカントール”