Delta-v_budget
アストロダイナミクスと航空宇宙では、デルタ v バジェットは、宇宙ミッションに必要な速度 (デルタ v)の合計変化の推定値です。これは、ミッション中に必要な各推進操作を実行するために必要なデルタ v の合計として計算されます。ツィオルコフスキー ロケット方程式への入力として、与えられた空の質量と推進システムのビークルに必要な推進剤の量を決定します。 Delta- v (フィート/秒)、および典型的なアポロ月面着陸ミッション
の燃料要件 デルタvは、宇宙船の質量ではなく、目的の軌道のみに依存するスカラー量です。たとえば、重い通信衛星を地球低軌道から静止軌道に移動させるには、軽い通信衛星よりも多くの燃料が必要ですが、必要なデルタvは同じです。ロケットの燃焼時間とは対照的に、 Delta- vも付加的であり、後者は、より多くの燃料が使い果たされたミッションの後半に大きな影響を与えます。
異なる宇宙体制の間を移動するために必要なデルタvの表は、宇宙ミッションの概念計画に役立ちます。大気がない場合、デルタvは通常、どちらの方向の軌道の変化でも同じです。特に、速度を上げることと下げることは、同じ労力を要します。大気は、エアロブレーキングによって宇宙船を減速させるために使用できます。
典型的な delta- v予算は、さまざまなクラスの操縦、操縦ごとの delta – v 、およびミッションの存続期間中に必要な各操縦の数を列挙し、典型的な財務予算と同様に、合計 delta- vを単純に合計します。ミッションを達成するために必要な delta-v は通常、重力体の相対位置によって異なるため、打ち上げ時間は、打ち上げ時間に対してプロットされたdelta – vを示すポークチョップ プロットから計算されることがよく
コンテンツ
1 一般原理
2 バジェット
2.1 打ち上げ・着陸 2.2 地球 – 月空間 – 高推力 2.3 地球 – 月空間 – 低推力 2.4 地球月面ゲートウェイ — 高推力 2.5 惑星間 2.6 地球、月、火星間のデルタ対 2.7 近地球天体
3 こちらもご覧ください
4 ノート
5 参考文献
6 外部リンク
一般原理
ツィオルコフスキー ロケットの式は、ロケット (ステージ) のデルタ v が、ロケットの燃料と空の質量比の対数、およびロケット エンジンの特定のインパルスに比例することを示しています。宇宙ミッションの軌道を設計する際の重要な目標は、必要なデルタ v を最小限に抑えて、特定のペイロードを目的地にうまく運ぶために必要なロケットのサイズと費用を削減することです。
最も単純なデルタ v バジェットは、ある円軌道から別の共面円軌道に楕円トランスファー軌道を介して移動するホーマン トランスファーを使用して計算できます。場合によっては、双楕円転送の方がデルタ v が低くなることが
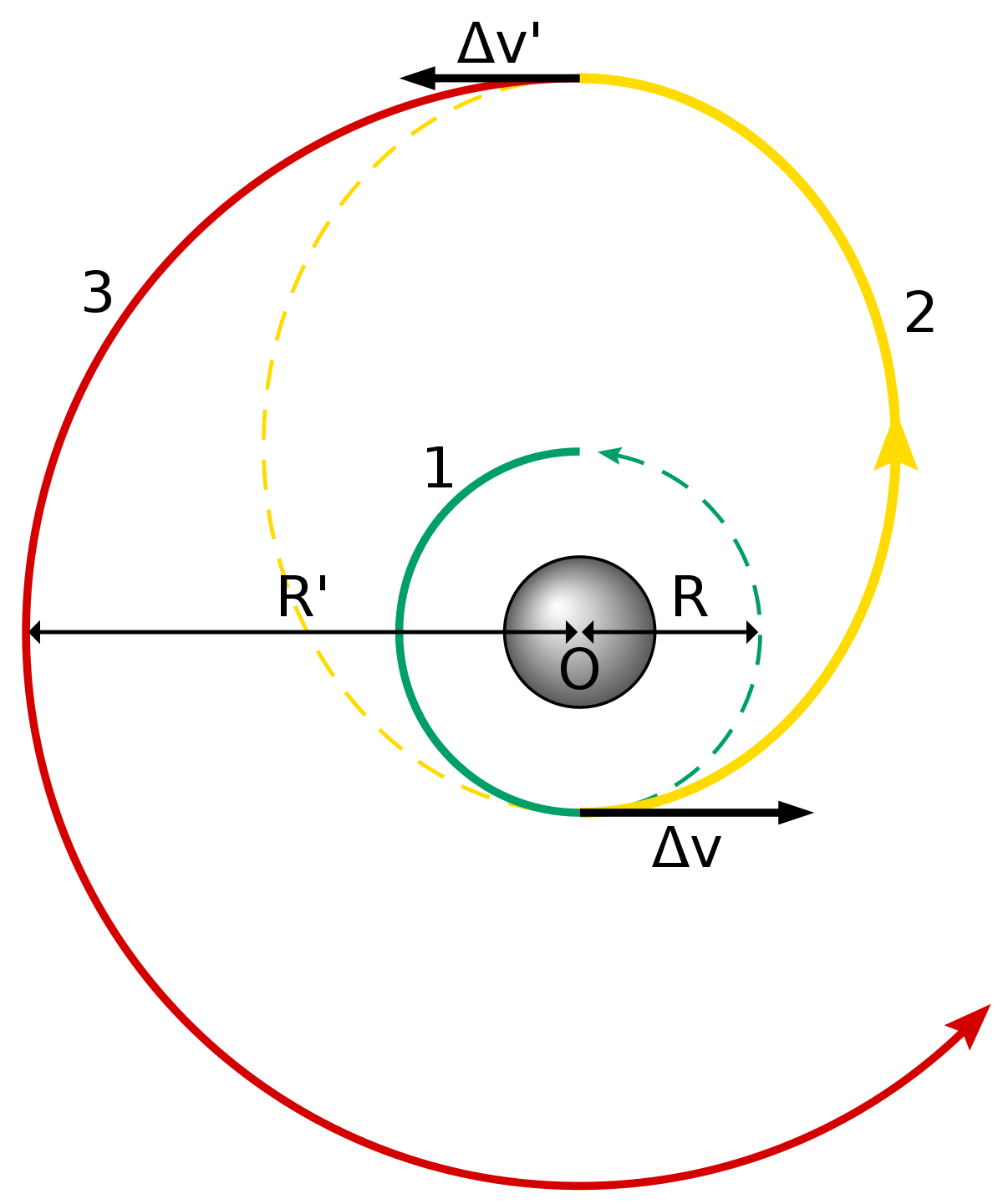
軌道 (1) からより高い軌道 (3) への 2 とラベル付けされたホーマン遷移軌道。これは、軌道間で非常に一般的に使用される操作です。
軌道が同一平面上にない場合、より複雑な移動が発生します。その場合、軌道の平面を変更するために必要な追加の delta-v がビークルの速度は、2 つの軌道面の交点でかなりの燃焼を必要とし、デルタ v は通常非常に高くなります。しかし、これらの平面の変化は、惑星体の重力と質量を使用してたわみを実行する場合、場合によってはほとんど自由にできる。他の場合では、比較的高い高度の遠点までブーストすると、飛行機の変更を実行する前に速度が低下するため、必要なデルタ v の合計が低くなります。
スリングショット効果を使用して、速度/エネルギーを高めることができます。車両が惑星または月体を通過すると、太陽または別の惑星に対するその物体の軌道速度の一部を拾う (または失う) 可能性が
もう 1 つの効果はオーベルト効果です。これを使用すると、必要なデルタ v を大幅に減らすことができます。これは、低ポテンシャル エネルギー/高速で推進剤を使用すると燃焼の効果が倍増するためです。したがって、たとえば、地球の軌道半径から火星の軌道半径への (太陽の重力を克服するための) ホーマン移動のデルタ v は、1 秒あたり数キロメートルですが、地球低軌道(LEO) からの増分燃焼は、克服するための燃焼を超えるものです。火星の移動軌道に到達するための燃焼が地球の軌道で行われるが、地球から遠く離れている場合よりも、燃焼が地球の近くで行われる場合、地球の重力ははるかに小さくなります。
あまり使用されない効果は、低エネルギー転送です。これらは、軌道共鳴によって機能し、ラグランジュ点に近い軌道を選択することによって機能する高度に非線形な効果です。それらは非常に遅くなる可能性がありますが、delta-v をほとんど使用しません。
delta-v は天体の位置と動きに依存するため、特にスリングショット効果とオーベルト効果を使用する場合、delta-v の予算は打ち上げ時間によって変化します。これらは、ポークチョップ プロットにプロットできます。
進路修正には、通常、推進剤の予算も必要です。推進システムは、常に正確な推進力を正確に正しい方向に提供することはなく、ナビゲーションも不確実性をもたらします。最適な軌道からの変動を修正するために、一部の推進剤を確保する必要が
バジェット

太陽系の選択された天体の Delta-v マップ。火傷は近点にあり、重力アシストと傾斜角の変化は無視されると仮定します(原寸)
打ち上げ・着陸
準軌道宇宙飛行のデルタ v 要件は、軌道宇宙飛行の場合よりもはるかに低くなります。Ansari X Prizeの高度 100 km に対して、Space Ship Oneは約 1.4 km/s のデルタ v を必要としました。国際宇宙ステーションの最初の地球低軌道300 km (現在は 400 km) に到達するには、デルタ v は 6 倍以上高く、約 9.4 km/s です。ロケット方程式の指数関数的な性質のため、軌道ロケットはかなり大きくする必要が
LEOへの打ち上げ— これには速度を 0 から 7.8 km/s に上げるだけでなく、通常、大気抵抗と重力抵抗のために 1.5 ~ 2 km/s にする必要があります
LEO からの再突入— 必要なデルタ v は、近地点を大気圏に降下させるための軌道操作燃焼であり、残りは大気抗力が処理します。
地球 – 月空間 – 高推力
地球-月系内を移動するのに必要なデルタ v (脱出速度 より遅い速度) は、km/s で与えられます。この表は、オーベルト効果が使用されていることを前提としています。これは、高推力の化学推進では可能ですが、現在 (2018 年現在) の電気推進では可能ではありません。
LEO の数値に戻ると、ヒート シールドとエアロブレーキング/エアロキャプチャーを使用して速度を最大 3.2 km/s 減速することを想定しています。熱シールドは、質量をおそらく 15% 増加させます。熱シールドが使用されていない場合、「LEO から」より高い Delta-v 値が適用されます。エアロブレーキを交換するために必要な追加の推進剤は、熱シールドよりも重い可能性がLEO-Ken は、ケネディ宇宙センターからの打ち上げに対応する、赤道に対して 28 度の傾斜角を持つ低地球軌道を指します。LEO-Eq は赤道軌道です。 q レオケン LEO-Eq ジオ EML-1 EML-2
EML-4/5LLO 月 C3=0
地球 9.3–10
地球低軌道(LEO-Ken).24 4.33 3.77 3.43 3.97 4.04 5.93 3.22 地球低軌道(LEO-Eq)4.24 .90 3.77 3.43 3.99 4.04 5.93 3.22 静止軌道(GEO)2.06 1.63 .38 1.47 1.71 2.05 3.92 1.30 ラグランジュ点 1 (EML-1)0.77 0.77 1.38 .14 0.33 0.64 2.52 0.14 ラグランジュ点 2 (EML-2)0.33 0.33 1.47 0.14 .34 0.64 2.52 0.14 ラグランジュ点 4/5 (EML-4/5)0.84 0.98 1.71 0.33 0.34 .98 2.58 0.43 月低軌道(LLO)0.90 0.90 2.05 0.64 0.65 0.98 .87 1.40 月面 2.742.74 3.92 2.52 2.53 2.58 1.87 .80
地球 脱出速度( C3 =0)0 01.30 0.14 0.14 0.43 1.40
2.80
地球 – 月空間 – 低推力
現在の電気イオンスラスターは非常に低い推力 (ミリニュートン、1 gのごく一部) を生成するため、オーベルト効果は通常使用できません。これにより、高推力の化学ロケットと比較して、より高いデルタvが必要になり、多くの場合、時間の大幅な増加が必要になります。それにもかかわらず、電気スラスターの高い比推力は、飛行のコストを大幅に削減する可能性が地球 – 月系でのミッションでは、有人宇宙飛行では移動時間が数日から数か月に増加することは受け入れられない可能性がありますが、惑星間飛行の飛行時間の違いはそれほど重要ではなく、有利になる可能性があります.
以下の表はデルタvを km/s で表したもので、通常は有効数字 2 桁まで正確で、上記の高推力セクションで説明したようにエアロブレーキングが使用されない限り、両方向で同じになります。
から デルタ v (km/s)
地球低軌道 (LEO)
地球-月ラグランジアン 1 (EML-1) 7.0 地球低軌道 (LEO)
静止地球軌道 (GEO) 6.0 地球低軌道 (LEO)
月低軌道 (LLO) 8.0 地球低軌道 (LEO)
太陽地球ラグランジアン 1 (SEL-1) 7.4 地球低軌道 (LEO)
太陽地球ラグランジアン 2 (SEL-2) 7.4 地球-月ラグランジアン 1 (EML-1)
月低軌道 (LLO)
0.60~0.80
地球-月ラグランジアン 1 (EML-1)
静止地球軌道 (GEO)
1.4–1.75
地球-月ラグランジアン 1 (EML-1)
太陽地球ラグランジアン 2 (SEL-2)
0.30~0.40
地球月面ゲートウェイ — 高推力
月のゲートウェイ宇宙ステーションは、月の周りの非常に楕円形の 7 日間のほぼ直線的なハロー軌道 (NRHO) に配備される予定です。地球から打ち上げられた宇宙船は、月のパワード フライバイを実行し、続いて NRHO 軌道挿入燃焼を実行して、軌道の遠点に近づくとゲートウェイとドッキングします。
から デルタ v (km/s)
地球低軌道 (LEO)
月横断噴射 (TLI) 3.20 月横断噴射 (TLI)
低(極)月軌道(LLO) 0.90 月横断噴射 (TLI)
月のゲートウェイ 0.43 月のゲートウェイ
低(極)月軌道 0.73 低(極)月軌道
月のゲートウェイ 0.73 月のゲートウェイ
アース インターフェイス (EI) 0.41
惑星間
宇宙船は、化学推進とオーベルト効果を使用していると想定されています。
から デルタ v (km/s)
レオ
火星トランスファー軌道
4.3 (「典型的」、最小ではない)
地球 脱出速度(C3=0)
火星 トランスファー軌道 0.6
火星 トランスファー軌道 火星 捕獲軌道 0.9
火星 捕獲軌道 ダイモス 転送軌道 0.2
ダイモス 転送軌道 ダイモス表面
0.7
ダイモス 転送軌道 フォボス 転送軌道 0.3
フォボス 転送軌道 フォボス表面
0.5
火星 捕獲軌道 火星低軌道
1.4
火星低軌道
火星表面
4.1
地球と月のラグランジュ点 2
火星トランスファー軌道
<1.0
火星トランスファー軌道
火星低軌道
2.7 (最低ではない)
地球 脱出速度(C3=0)
最も近いNEO
0.8–2.0
マースデンとロスによると、「太陽と地球の L 1点と L 2点のエネルギー レベルは、地球と月のシステムのエネルギー レベルとわずか 50 m/s しか違いません (マニューバ速度で測定)」。
式を適用する場合があります△ v = μ r 1 (2
r2 r 1 + r 2 −1 )
{ Delta v={sqrt {frac {mu }{r_{1}}}}left({sqrt {frac {2r_{2}}{r_{1}+r_{2} }}}-1右)}
(ここで、μ = GM は太陽の標準的な重力パラメーターです。ホーマン伝達軌道を参照してください)地球からさまざまな目的地に到着するために必要なΔ v (km/s 単位) を計算します (惑星の軌道が円形であると仮定し、冥王星の近日点距離を使用します)。 )。この表では、「地球の軌道からホーマン軌道に入るΔ v 」というラベルの付いた列は、地球の速度からホーマン楕円に乗るのに必要な速度までの変化を示しています。””v exiting LEO”” というラベルの付いた列は、地球の表面から 300 km 上空にある場合に必要な速度 (地球を中心とする非回転座標系) を示しています。これは、比運動エネルギーに、この地球低軌道の速度 (7.73 km/s) の 2 乗 (つまり、この LEO における地球の重力の深さ) を加えることによって得られます。「Δ v from LEO」という列は、単純に以前の速度から 7.73 km/s を引いたものです。通過時間は次のように計算されます。( ( 1 + 軌道半径) / 2 ) 3 / 2/ 2
{ ((1+{text{軌道半径}})/2)^{3/2}/2}
年。
表の値は、惑星の軌道距離に到達するために必要な Δv のみを示していることに注意して惑星に対する相対的な速度は依然としてかなりのものであり、惑星の周りの軌道に入るには、惑星の大気を使用した航空捕獲が必要になるか、より多くの Δv が必要になります。
行き先
軌道半径( AU )
地球軌道からホーマン軌道に入るΔv
LEOを出るΔv
LEOからのΔv
輸送時間
太陽 029.8 31.7 24.0
2.1ヶ月
水星 0.397.5 13.3 5.5
3.5ヶ月
金星 0.722.5 11.2 3.5
4.8ヶ月
火星 1.522.9 11.3 3.6
8.5ヶ月
木星 5.28.8 14.0 6.3
2.7年
土星 9.5410.3 15.0 7.3
6.0年
天王星 19.1911.3 15.7 8.0
16.0年
ネプチューン 30.0711.7 16.0 8.2
30.6年
冥王星 29.66(周辺)11.6 16.0 8.2
45.5年
1光年 63,24112.3 16.5 8.8
280万年
冥王星へのニュー ホライズンズ宇宙探査機は、太陽から逃れるのに十分な 16 km/s 以上の近地球速度を達成しました。(木星のフライバイの影響も受けています。)
太陽に到達するために、実際には 24 km/s のΔ vを使用する必要はありません。8.8 km/s を使用して太陽から非常に遠くに移動し、無視できる Δ vを使用して角運動量をゼロにしてから、太陽に落ちることができます。これは、1 回がアップ、もう 1 回がダウンの 2 つのホーマン転送のシーケンスと見なすことができます。また、この表には、月を重力アシストに使用する場合に適用される値は示され他の惑星や太陽への到達を支援するために、最も到達しやすい金星のような 1 つの惑星を使用する可能性もガリレオ探査機は、木星に到達するために金星を 1 回、地球を 2 回使用しました。ユリシーズ太陽探査機は、木星を使用して太陽の周りの極軌道に到達しました。
地球、月、火星間のデルタ対

Delta-v は、従来のロケットを使用したさまざまな軌道操作に必要です。
略語キー
低周心で軌道を脱出– C3 = 0
静止軌道– GEO
静止トランスファー軌道– GTO
地球–月L 5 ラグランジュ点– L5
地球低軌道– LEO
月軌道とは、月の低軌道を意味します。
赤い矢印は、その特定の方向でオプションのエアロブレーキング/エアロキャプチャを実行できる場所を示し、黒い数字は、どちらの方向にも適用される km/s 単位のデルタ v を示します。多くの場合、示されているよりも低いデルタ v 転送を実現できますが、まれな転送ウィンドウを伴うか、大幅に時間がかかります。ファジー軌道転送を参照して
オーベルト効果を使用せずに火星 C3 = 0 から地球 C3 = 0 に移動する電気推進車両には、2.6 km/s から 3.15 km/s の間のより大きな Delta-v が必要です。すべての可能なリンクが示されているわけではありません。
C3 = 0 から火星への移動の Delta-v は、中心点で、つまり脱出軌道に加速した直後に適用する必要があり、地球からの脱出から 0.4、火星からの脱出から 0.65 を与える上記の式と一致しません。
LEO から GTO、GTO から GEO、LEO から GEO の数値は一致しません。太陽に対するしし座の 30 という数値も高すぎます。
近地球天体
地球近傍天体は、軌道が地球から約 0.3天文単位以内に収まる小惑星です。月や火星よりも到達しやすいそのような天体は何千もLEO からの一方向のデルタ v バジェットは 3.8 km/s (12,000 フィート/秒) 以上の範囲であり、月面に到達するのに必要なデルタ v の 2/3 未満です。しかし、デルタ v バジェットが低い NEO は会議期間が長く、地球への最接近 (したがって最も効率的なミッション) の間隔は数十年にも及ぶ可能性が
地球に近いオブジェクトから戻るために必要なデルタ v は、通常は非常に小さく、地球の大気を使用した航空写真では 60 m/s (200 フィート/秒) になることもただし、これには熱シールドが必要であり、質量が増加し、宇宙船の形状が制約されます。軌道の位相は問題になる可能性がランデブーが達成されると、体によっては、低デルタ-V リターン ウィンドウがかなり離れている可能性があります (1 年以上、多くの場合、何年も)。
一般に、地球よりもはるかに遠くまたは太陽に近い天体は、移動のための窓がより頻繁にありますが、通常はより大きなデルタ対が必要です。
こちらもご覧ください
![]()
宇宙飛行ポータル
双楕円転送
重力アシスト
ホーマン転移
オーベルト効果
軌道速度
ツィオルコフスキーロケット方程式
ポークチョッププロット
会議期間
ノート
^ LEO から GTO および GTO から GEO の合計は、LEO から GEO に等しくなければなりません。正確な数値は、どの地球低軌道が使用されているかによって異なります。静止トランスファー軌道によると、近地点での GTO の速度はわずか 9.8 km/s です。これは、高度約 700 km の LEO に相当し、その速度は 7.5 km/s であり、デルタ v は 2.3 km/s になります。低い LEO から開始すると、GTO に到達するにはより多くのデルタ v が必要になりますが、LEO から GEO までの合計はより高くする必要が ^ 太陽の周りを公転する地球の速度は、平均して秒速 29.78 km で、比運動エネルギー 443 km 2 /秒2に相当します。31.8 km/s の速度に対応する504 km 2 /s 2の地球に近い運動エネルギーを与えるには、これに LEO の位置エネルギー深さ、約 61 km 2 /s 2を追加する必要がLEO の速度は 7.8 km/s であるため、delta-v はわずか 24 km/s です。重力アシストを使用すると、より少ないデルタ v で太陽に到達することが可能になります。パーカーソーラープローブを参照して太陽から遠く離れて (Δv 8.8 km/s)、非常に小さな Δv を使用して角運動量を打ち消し、太陽に落ちるという長い道のりをたどることも可能です。
参考文献
^ Robert W. Farquhar (1972 年 6月)。「ハロー軌道月面ステーション」 (PDF) . 宇宙工学と航空学。10 (6): 59–63. 2015-12-25のオリジナル (PDF)からのアーカイブ。2016 年3 月17 日閲覧。
^ FISO「ゲートウェイ」コンセプト 2010、さまざまな著者の 26 ページ 2012 年 4 月 26 日、Wayback Machineでアーカイブ
^ ホイットリー、ライアン。マルティネス、ローランド (2015 年 10 月 21 日)。「Cis-Lunar 空間におけるステージング軌道のオプション」 (PDF) . nasa.gov . ナサ。2018年9 月 19 日閲覧。
^ フランク・ゼグラー; バーナード・クッター(2010)。「デポベースの宇宙輸送アーキテクチャへの進化」 (PDF) . 2011 年 10 月 20 日にオリジナル (PDF)からアーカイブされました。
^ i
「ロケットと宇宙輸送」 . 2007 年 7 月 1 日にオリジナルからアーカイブされました。2013年6 月 1 日閲覧。
^「NEOリスト」 . 2001-06-03のオリジナルからのアーカイブ。
^ 「天体力学とミッション設計の新しい方法」 . ブル。アメール。算数。社会
^ 「デルタV電卓」 . 2000 年 3 月 12 日にオリジナルからアーカイブされました。地表から LEO までは 8.6、LEO から月軌道 (または L5) までは 4.1 と 3.8、GEO はそれぞれ 0.7、L5 から月軌道までは 0.7、月軌道から月面までは 2.2 の数値を与える。図は、NASA の Web サイトにあるSpace Settlements: A Design Studyの第 2 章からのものです。
^”「火星サンプル リターン ミッションのイオン推進」ジョン R. ブロフィーとデビッド H. ロジャース、AIAA-200-3412、表 1″ (PDF) . 2011 年 8 月 7 日にオリジナル (PDF)からアーカイブされました。
^ 「宇宙船ランデブーのための近地球小惑星デルタ-V」 . JPL NASA. 2001-06-03のオリジナルからのアーカイブ。
^「小惑星ランデブー軌道の調査」 . ccar.colorado.edu。2017-04-10のオリジナルからのアーカイブ。2017 年 2月2 日閲覧。
^「NASA、惑星間航海を計画するための新しいウェブサイトを立ち上げ」 . スペース.com . 2017 年 2月2 日閲覧。
外部リンク
JavaScript デルタ V 計算機
装飾デルタ V マップ
原子ロケット – ミッションは何ですか? delta-v の長い Web ページ (ソースではありません – を引用しています)”