Demihypercube
Hemicube (ジオメトリ)
と混同しないでください 幾何学では、デミハイパーキューブ (n-デミキューブ、n-ヘミキューブ、ハーフ メジャー ポリトープとも呼ばれます) は、n-ハイパーキューブの交替から構築されたn-ポリトープのクラスであり、ハイパーキューブ ファミリーの半分であるγ nとしてhγ nとラベル付けされています。 . 頂点の半分が削除され、新しいファセットが形成されます。2 n 個のファセットは 2 n ( n −1)-デミキューブ、および 2 n ( n −1) – シンプレックスファセットが、削除された頂点の代わりに形成されます。
3-立方体の
3-デミキューブとして生じる
2 つの四面体の3 次元図のように
、 n-立方体の交替により
、2 つの
n-デミキューブのうちの 1 つが生成されます。
デミキューブは通常の四面体と同じで、デミテセラクトは通常の16 セルと同じです。半透膜は、規則的なファセットのみを持つため、半規則的であると見なされます。高次の形は、すべてが規則的なファセットを持っているわけではありませんが、すべて均一なポリトープです。
準超立方体の頂点とエッジは、半分に分割された立方体グラフの 2 つのコピーを形成します。
nが偶数の場合、nデミキューブは反転対称性を持ちます。
コンテンツ
1 発見
2 構造
3 対称群
4 同所性構造
5 こちらもご覧ください
6 参考文献
7 外部リンク
発見
Thorold Gossetは、1900 年の出版物で、 3 次元以上のn次元のすべての正則図形と半正則図形をリストした半中間体について説明しました。彼はそれを5-ic 準正則と呼びました。また、半規則的なk 21ポリトープファミリー内にも存在します。
半超立方体は、{4，3，…，3} の半分の頂点として h{4，3，…，3} の形式の拡張シュレーフリ記号で表すことができます。半超立方体の頂点図形は修正された n-シンプレックスです。
構造
これらは、次の 3 つの構成形式のCoxeter-Dynkin ダイアグラムによって表されます。
.. (代替 同位体として) s{2 1，1，…，1 }
..
(交互超立方体として) h{4，3 n −1 }
..
. (半超立方体として) {3 1， n −3，1 }
HSM Coxeterはまた、3 番目の分岐図に1 k 1というラベルを付け、3つの枝の長さを表し、環状の枝が先導しました。
nデミキューブ( nが 2 より大きい) には、各頂点で接するn ( n −1)/2 個のエッジが以下のグラフは、対称投影でエッジが重なっているために、各頂点のエッジが少ないことを示しています。
n 1k1 _ _ ペトリポリゴン シュレフリ記号 コクセター線図A 1 n B n D n
要素
ファセット:デミハイパーキューブ &シンプレックス
頂点図
頂点
エッジ 顔
細胞4面 5面 6面 7面 8面 9面
2 1 −1，1
デミススクエア(ディゴン)
s{2} h{4} {3 1，−1，1 }
2 2
2 つのエッジ —
3 1 01
デミキューブ（四面体）
s{2 1，1 } h{4，3} {3 1，0，1 }
4 6 4
(6角形) 4 つの三角形 トライアングル（直角三角形）
4 1 11
デミセラクト( 16セル)
s{2 1，1，1 } h{4，3，3} {3 1，1，1 }
8 24 32 16
8 個のデミキューブ(四面体) 8個の四面体 八面体（正四面体）
5 1 21
半腸骨
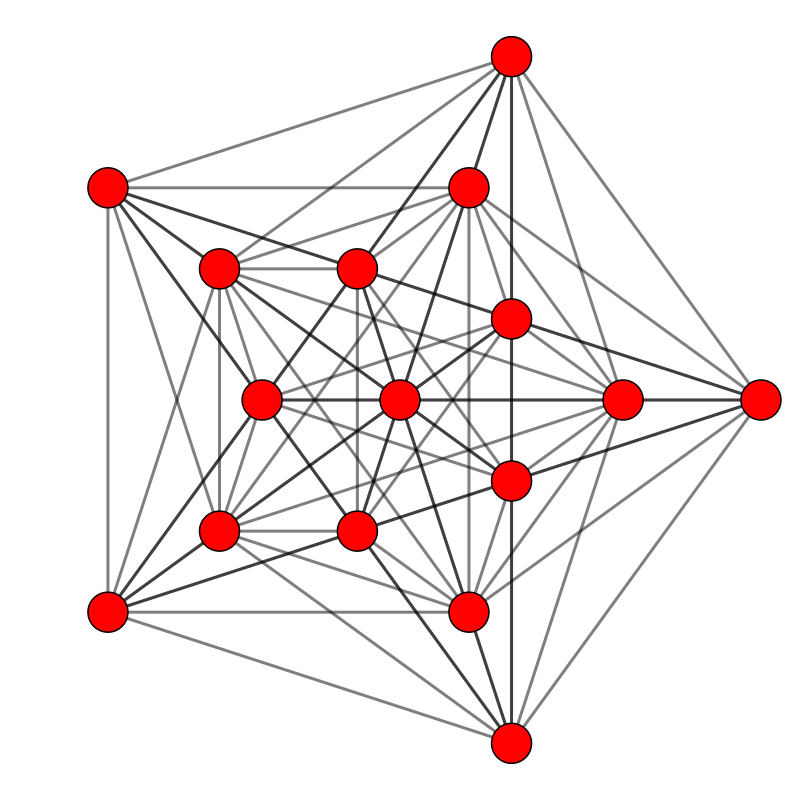
s{2 1，1，1，1 } h{4，3 3 }{3 1，2，1 }
16 80 160 120 26
10 16 セル16 5 セル 整流 5 セル
6 1 31
デミヘキサラクト
s{2 1，1，1，1，1 } h{4，3 4 }{3 1，3，1 }
32 240 640 640 252 44
12個の半腸類32個の5-シンプリス 整流ヘキサテロン
7 1 41
半ヘプタラクト
s{2 1，1，1，1，1，1 } h{4，3 5 }{3 1，4，1 }
64 672 2240 2800 1624 532 78
14デミヘキサラクト64 6-シンプリス 修正された 6 シンプレックス
8 1 51
八角形
s{2 1，1，1，1，1，1，1 } h{4，3 6 }{3 1，5，1 }
128 1792年7168 10752 8288 4032 1136 144
16デミヘプタラクト128 7-シンプリックス 修正された 7 シンプレックス
9 1 61
半端者
s{2 1，1，1，1，1，1，1，1 } h{4，3 7 }{3 1，6，1 }
256 4608 21504 37632 36288 23520 9888 2448 274
18デミオクテラクト256 8-シンプリス 修正された 8 シンプレックス
10 1 71
デミデケラクト
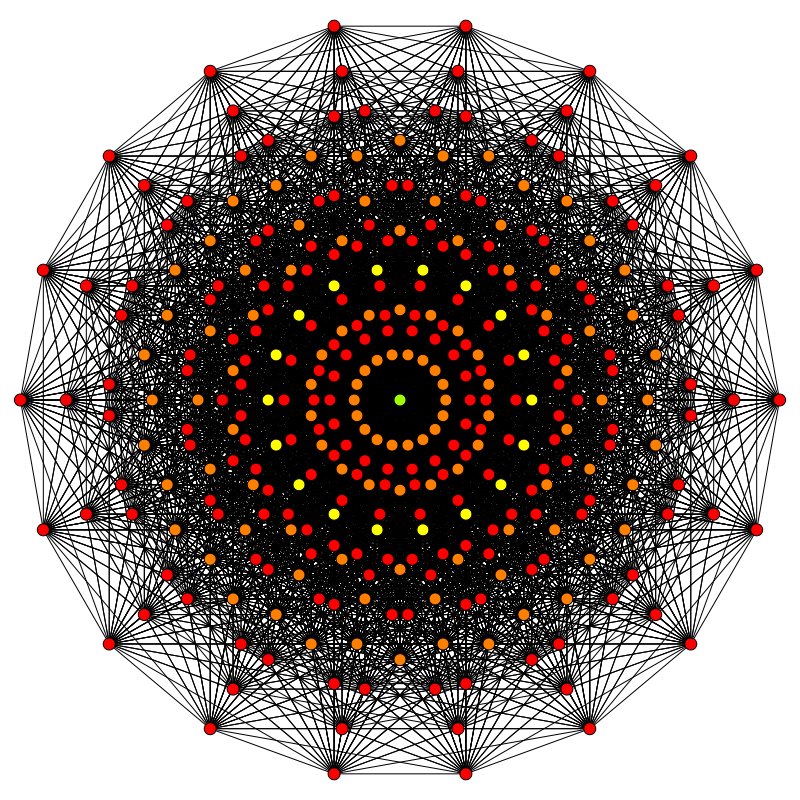
s{2 1，1，1，1，1，1，1，1，1 } h{4，3 8 }{3 1，7，1 }
512 11520 61440 122880 142464 115584 64800 24000 5300 5120
20個のデミネナクト512 個の 9-単純化 修正された 9 シンプレックス
…
n 1 n −3，1
n-デミキューブ s{2 1，1，…，1 } h{4，3 n −2 }{3 1， n −3，1 }
…
…
…
2 n −1
2 n ( n −1)-デミキューブ2 n −1 ( n −1)-単純化 Rectified ( n −1)-シンプレックス
一般に、デミキューブの要素は、元のnキューブから決定できます。_ _ _ )
頂点: D n ，0 = 1/2 C n ，0 = 2 n −1 ( n立方体の頂点の半分が残る)
エッジ: D n ，1 = C n ，2 = 1/2 n ( n −1) 2 n −2 (元のエッジはすべて失われ、正方形の面ごとに新しいエッジが作成されます)
面: D n ，2 = 4 * C n ，3 = 2/3 n ( n −1)( n −2) 2 n −3 (元の面はすべて失われ、立方体ごとに 4 つの新しい三角形面が作成されます)
セル: D n ，3 = C n ，3 + 2 3 C n ，4 (元のセルと新しいセルの四面体)
ハイパーセル: D n ，4 = C n ，4 + 2 4 C n ，5 (それぞれ 16 セルと 5 セル)
…
[For m = 3，…， n −1]: D n ， m = C n ， m + 2 m C n ， m +1 (それぞれm -デミキューブとm -シンプレックス)
…
ファセット: D n ， n −1 = 2 n + 2 n −1 (( n −1)-デミキューブおよび ( n −1)-シンプリス)
対称群
超八面体群(コクセター群)における半超立方体の安定剤B ハ n
{ BC_{n}}
) のインデックスは 2 です。これはコクセター群です。 D n { D_{n}，}