Double_pendulum
物理学と数学では、力学系の分野では、二重振り子は振り子の端にもう 1 つの振り子が取り付けられたもので、初期条件に強い感度を持つ豊かな動的挙動を示す単純な物理システムを形成します。二重振り子の運動は、結合された一連の常微分方程式によって支配され、カオスです。
二重振り子は、
端と端を
つないだ2つの振り子で構成されています。
コンテンツ
1 分析と解釈
1.1 ラグランジアン
2 カオスモーション
3 こちらもご覧ください
4 ノート
5 参考文献
6 外部リンク
分析と解釈
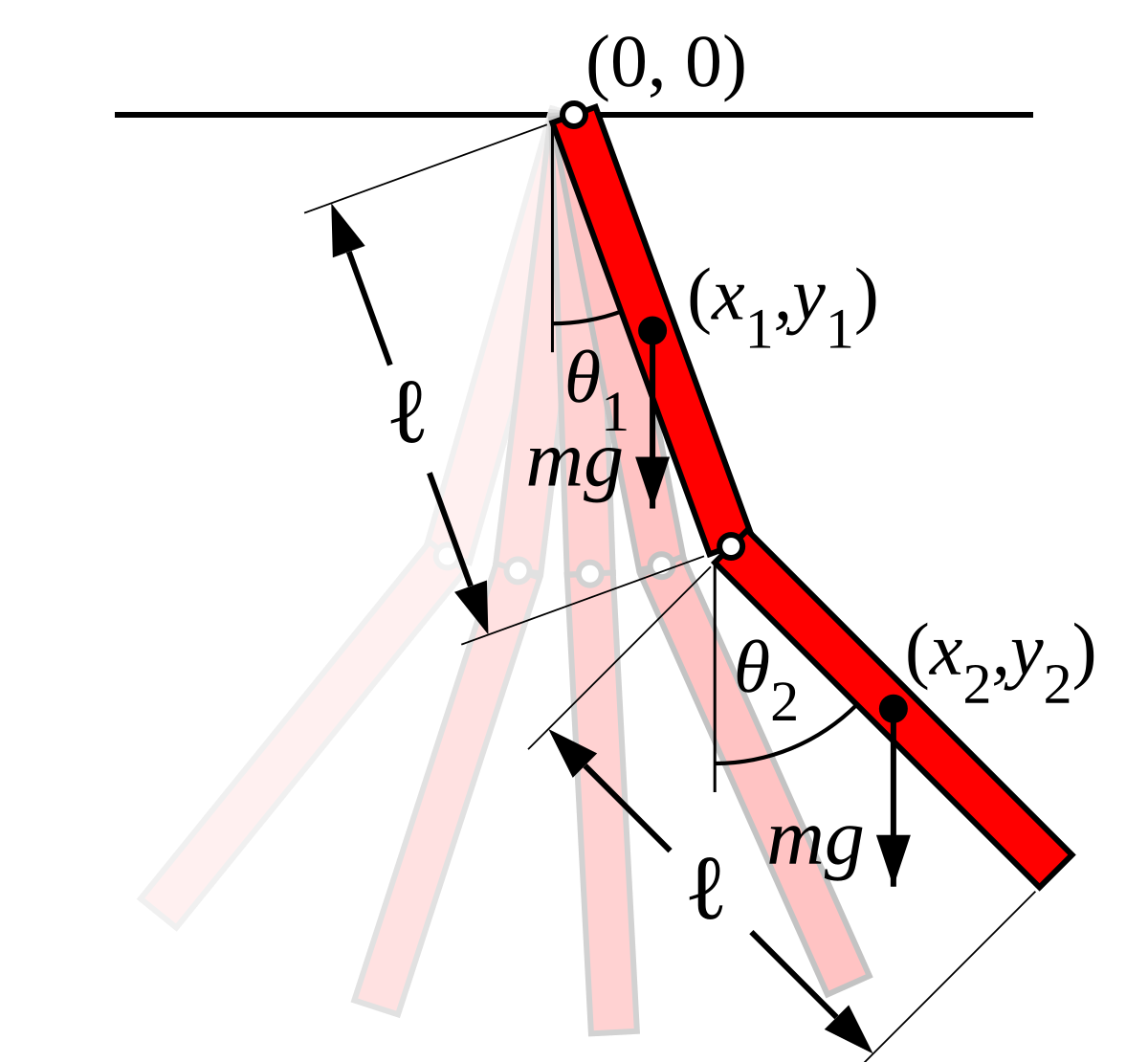
二重振り子のいくつかの変形が考えられます。2 本の手足は、長さと質量が同じでも等しくなくてもよく、単純な振り子または複合振り子(複雑な振り子とも呼ばれます) である場合もあり、動きが 3 次元または垂直面に制限されている場合も次の分析では、四肢は長さlと質量mの同一の複合振り子であると見なされ、運動は 2 次元に制限されます。
二重複式振り子

二重複式振り子
の運動(運動方程式の
数値積分より)
二重振り子の軌道
複合振り子では、質量はその長さに沿って分布します。質量が均等に分布している場合、各リムの重心はその中間点にあり、リムの慣性モーメントはI =1/12ml 2その点について。
システムの構成を定義する一般化された座標として、各肢と垂直の間の角度を使用すると便利です。これらの角度は、θ 1およびθ 2で示される。各ロッドの重心の位置は、これらの 2 つの座標で記述できます。デカルト座標系の原点が最初の振り子の吊り点にあると見なされる場合、この振り子の重心は次の場所にX1 = l 2
sin θ1 y 1 = − l 2
コスθ 1
{ {begin{aligned}x_{1}&={frac {l}{2}}sin theta _{1}\y_{1}&=-{frac {l}{2 }}costheta_{1}end{整列}}}
そして、2 番目の振り子の重心はX2 = l( sinθ 1 +1 2 sinθ 2) y 2 = − l ( コス +1 2 コス ) { {begin{aligned}x_{2}&=lleft(sin theta _{1}+{tfrac {1}{2}}sin theta _{2}right) y_{2}&=-lleft(cos theta _{1}+{tfrac {1}{2}}cos theta _{2}right)end{aligned}}}
これは、ラグランジアンを書き出すのに十分な情報です。
ラグランジアン
ラグランジアンは_L =
運動エネルギー − 位置エネルギー =1 2 メートル( v1 2+ v2 2 )+1 2 I ( θ
˙1 2+ θ
˙2 2) −
メートル g ( y1 + y 2 ) =1 2 メートル (X ˙1 2+ y
˙1 2 +X ˙2 2+ y
˙2 2 ) +1 2 I ( θ
˙1 2+ θ
˙2 2) −
メートル g ( y1 + y 2 )
{ {begin{aligned}L&={text{運動エネルギー}}-{text{位置エネルギー}}\&={tfrac {1}{2}}mleft(v_{1} ^{2}+v_{2}^{2}right)+{tfrac {1}{2}}Ileft({{dot {theta}}_{1}}^{2}+ {{dot {theta }}_{2}}^{2}right)-mgleft(y_{1}+y_{2}right)\&={tfrac {1}{2 }}mleft({{dot {x}}_{1}}^{2}+{{dot {y}}_{1}}^{2}+{{dot {x}} _{2}}^{2}+{{dot {y}}_{2}}^{2}right)+{tfrac {1}{2}}Ileft({{dot { theta }}_{1}}^{2}+{{dot {theta }}_{2}}^{2}right)-mgleft(y_{1}+y_{2} right)end{aligned}}}
最初の項は物体の質量中心の線形 運動エネルギーで、2 番目の項は各ロッドの質量中心の周りの回転運動エネルギーです。最後の項は、一様な重力場における物体の位置エネルギーです。ドット表記は、問題の変数の時間導関数を示します。
上記の座標を代入して式を整理すると、 L =1 6
メートルl 2( θ
˙2 2 4 θ ˙1 2 3θ ˙
1θ ˙ 2 コス(θ1 θ 2)
) 1 2
メートルg l ( 3 コス
θ1
コスθ 2 ) . { L={tfrac {1}{6}}ml^{2}left({{dot {theta }}_{2}}^{2}+4{{dot {theta }}_{1}}^{2}+3{{dot {theta}}_{1}}{{dot {theta}}_{2}}cos(theta_{1} -theta _{2})right)+{tfrac {1}{2}}mglleft(3cos theta _{1}+cos theta _{2}right)}
保存される量 (エネルギー) は 1 つだけで、運動量は保存されません。2 つの一般化された運動量は、次のように記述できます。p θ
1= ∂ L ∂ θ ˙ 1 =1 6 メートルl 2( 8θ ˙ 1 + 3 θ ˙ 2 コス ( θ 1− θ
2) ) p θ
2= ∂ L ∂ θ ˙ 2 =1 6 メートルl 2( 2θ ˙ 2 + 3 θ ˙ 1 コス ( θ 1− θ
2) ) .
{ {begin{aligned}p_{theta _{1}}&={frac {partial L}{partial {{dot {theta }}_{1}}}}={ tfrac {1}{6}}ml^{2}left(8{{dot {theta}}_{1}}+3{{dot {theta}}_{2}}cos( theta _{1}-theta _{2})right)\p_{theta _{2}}&={frac {partial L}{partial {{dot {theta }} _{2}}}}={tfrac {1}{6}}ml^{2}left(2{{dot {theta}}_{2}}+3{{dot {theta }}_{1}}cos(theta _{1}-theta _{2})right).end{整列}}}
これらの式は、取得するために逆にすることができます θ ˙1 6
メートルl 2 p θ
1− 3
コス( θ 1 − 2) p
θ 16− 9
コス 2 ( θ 1 − 2) θ
˙2 6
メートルl 8 p θ
2− 3
コス( θ 1 − 2) p
θ 16− 9
コス 2 ( θ 1 − 2) .
{ {begin{aligned}{{dot {theta }}_{1}}&={frac {6}{ml^{2}}}{frac {2p_{theta _{1 }}-3cos(theta _{1}-theta _{2})p_{theta _{2}}}{16-9cos ^{2}(theta _{1}-シータ _{2})}}\{{dot {シータ }}_{2}}&={frac {6}{ml^{2}}}{frac {8p_{シータ _{ 2}}-3cos(theta _{1}-theta _{2})p_{theta _{1}}}{16-9cos ^{2}(theta _{1}- theta _{2})}}.end{整列}}}
残りの運動方程式は次のように書かれます。p ˙ θ 1 = ∂ L
∂ 1 = − 2
メートルl 2( θ˙ 1 θ ˙ 2
sin ( θ
1− θ
2) + 3 g l sinθ
1 ) p˙ θ 2 = ∂ L
∂ 2 = − 2
メートルl 2( −θ ˙ 1 θ ˙ 2
sin ( θ
1− θ
2) + g l sinθ
2) .
{ {begin{aligned}{{dot {p}}_{theta _{1}}}&={frac {partial L}{partial theta _{1}}}=- {tfrac {1}{2}}ml^{2}left({{dot {theta }}_{1}}{{dot {theta }}_{2}}sin( theta _{1}-theta _{2})+3{frac {g}{l}}sin theta _{1}right)\{{dot {p}}_{theta _{2}}}&={frac {partial L}{partial theta _{2}}}=-{tfrac {1}{2}}ml^{2}left(-{{ dot {theta }}_{1}}{{dot {theta }}_{2}}sin(theta _{1}-theta _{2})+{frac {g} {l}}sin theta _{2}right).end{aligned}}}
これらの最後の 4 つの方程式は、現在の状態が与えられたシステムの時間発展の明示的な公式です。さらに進んで、これらの方程式を閉じた形式の式に統合して、時間の関数としてθ 1とθ 2の式を取得することはできません 。ただし、ルンゲ クッタ法または類似の手法を使用して、この積分を数値的に実行することは可能です。
カオスモーション

振り子がひっくり返るまでの時間を初期条件の関数として表したグラフ

無秩序な動きを示す二重振り子の長時間露光 ( LEDで追跡)
二重振り子はカオス運動を起こし、初期条件に敏感に依存します。右の画像は、振り子がひっくり返るまでの経過時間を、静止状態で解放されたときの初期位置の関数として示しています。ここで、 θ 1の初期値はx方向に沿って-3.14 から 3.14 の範囲です。初期値θ 2の範囲はy方向に沿って、-3.14 から 3.14 です。各ピクセルの色は、振り子が内側で反転するかどうかを示します。
l g { {sqrt {frac {l}{g}}}}
(黒)10 l g
{ 10{sqrt {frac {l}{g}}}}
(赤)100 l g
{ 100{sqrt {frac {l}{g}}}}
(緑)1000 l g
{ 1000{sqrt {frac {l}{g}}}}
(青)または10000 l g
{ 10000{sqrt {frac {l}{g}}}}
(紫の)。

ほぼ同一の初期条件を持つ 3 つの二重振り子は、システムの混沌とした性質を示す時間の経過と共に発散します。
内で反転につながらない初期条件10000 l g
{ 10000{sqrt {frac {l}{g}}}}
白でプロットされます。
中央の白い領域の境界は、次の曲線のエネルギー保存によって部分的に定義されます。 3 コス θ 1 + コス θ 2= 2.
{ 3cos theta _{1}+cos theta _{2}=2.}
この曲線によって定義された領域内で、つまり 3 コス θ 1 + コス θ 2 > 2 { 3cos theta _{1}+cos theta _{2}>2,}
2,}””>
その場合、どちらの振り子も反転することはエネルギー的に不可能です。この領域の外では、振り子は反転する可能性がありますが、いつ反転するかを判断するのは複雑な問題です。同様の挙動は、質量が分散された 2 本の棒ではなく、2 つの質量点で構成される二重振り子でも観察されます。
自然励振周波数の欠如は、建物自体が一次倒立振子であり、二次質量が接続されて二重振り子を完成させる、建物の耐震設計に二重振り子システムを使用することにつながりました。
こちらもご覧ください
二重倒立振子
振り子(力学)
20 世紀半ばの物理学の教科書では、「二重振り子」という用語を使用して、V 字型のストリングから吊り下げられたストリングから吊り下げられた単一のボブを意味します。リサージュ曲線を生成するこのタイプの振り子は、現在、ブラックバーン振り子と呼ばれています。
ノート
^ レビエン、RB; タン、SM (1993)。「二重振り子: カオスの実験」. 物理学のアメリカのジャーナル。61 (11): 1038. Bibcode : 1993AmJPh..61.1038L . ドイ: 10.1119/1.17335 . ^ Alex Small、 Sample Final Project: One Signature of Chaos in the Double Pendulum、(2013). 学生向けの例として作成されたレポート。運動方程式の導出、および 2 つの点質量を持つ二重振り子と 2 つの棒を持つ二重振り子の比較が含まれます。
参考文献
マイロビッチ、レナード(1986)。振動解析の要素(第 2 版)。マグロウヒル科学/工学/数学. ISBN 0-07-041342-8.
Eric W. Weisstein, Double pendulum (2005), ScienceWorld (関連する複雑な方程式の詳細を含む)およびRob Morris による” Double Pendulum “, Wolfram Demonstrations Project , 2007 (これらの方程式のアニメーション).
ピーター・リンチ、二重振り子、(2001)。(Java アプレットのシミュレーション。)
Northwestern University、Double Pendulum、(Java アプレット シミュレーション)。
UBC の理論的高エネルギー天体物理学グループ、二重振り子、(2005)。
外部リンク
Mike Wheatland (Univ. Sydney) による二重振り子と物理的な二重振り子 (2 つの正方形プレート)のアニメーションと説明
詳細な方程式を使用したインタラクティブなオープンソース物理 JavaScript シミュレーション二重振り子
二重振り子の対話型 Javascript シミュレーション
オープン ソースの JavaScript コードを使用したwww.myphysicslab.comの二重振り子物理シミュレーション
ロットの振り子のシミュレーション、方程式、説明
YouTubeに同じ初期始動条件の二重振り子の比較動画
Double Pendulum Simulator – Qt ツールキットを使用してC++で記述されたオープン ソース シミュレーター。
イマジナリー展のオンラインJavaシミュレーター。”