Green’s_law
は、流体力学の法則についてです。グリーンの定理と混同しないでください 流体力学では、19世紀の英国の数学者ジョージグリーンにちなんで名付けられたグリーンの法則は、深さと幅が徐々に変化する浅瀬を伝播する非破壊の表面重力波の進化を説明する保存則です。最も単純な形式では、互いに平行な波面と深さの等高線(および海岸)について、次のように述べています。
水深の減少に伴う
波長と
波高の変化を示す、浅瀬の長い波の伝播 H1 ⋅ h1 4 = H 2 ⋅ h2 4 { H_ {1} 、 cdot 、{ sqrt {h_ {1}}} = H_ {2} 、 cdot 、{ sqrt {h_ { 2}}}}
また ((H
1)。4 ⋅ h 1 = ((H 2)。4 ⋅ h
2 { left(H_ {1} right)^ {4} 、 cdot 、h_ {1} = left(H_ {2} right)^ {4} 、 cdot 、h_ { 2}、}
どこH 1
{ H_ {1}}と H 2
{ H_ {2}}
は、波が通過する2つの異なる場所(それぞれ1と2)での波の高さです。h 1
{ h_ {1}}と h 2
{ h_ {2}}
同じ2つの場所での平均水深です。
グリーンの法則は、海岸工学でビーチでの長い浅瀬の波のモデリングによく使用されます。「長い」とは、平均水深の約20倍を超える波長を意味します。 津波は、屈折と回折によって支配され、海を越えて大陸棚を上って伝播するため、この法則に従って浅瀬になります(高さを変更します)。海岸に非常に近い(そして走り上がる)と、非線形効果が重要になり、グリーンの法則は適用されなくなります。
コンテンツ
1 説明
1.1 波長と周期
2 導出
2.1 開水路の波動方程式 2.2 独立変数としての波動位相への変換 2.3 均質性へのさらなる変革 2.4 正弦波とグリーンの法則 2.5 流速
3 ノート
4 参考文献
4.1 緑 4.2 その他
説明
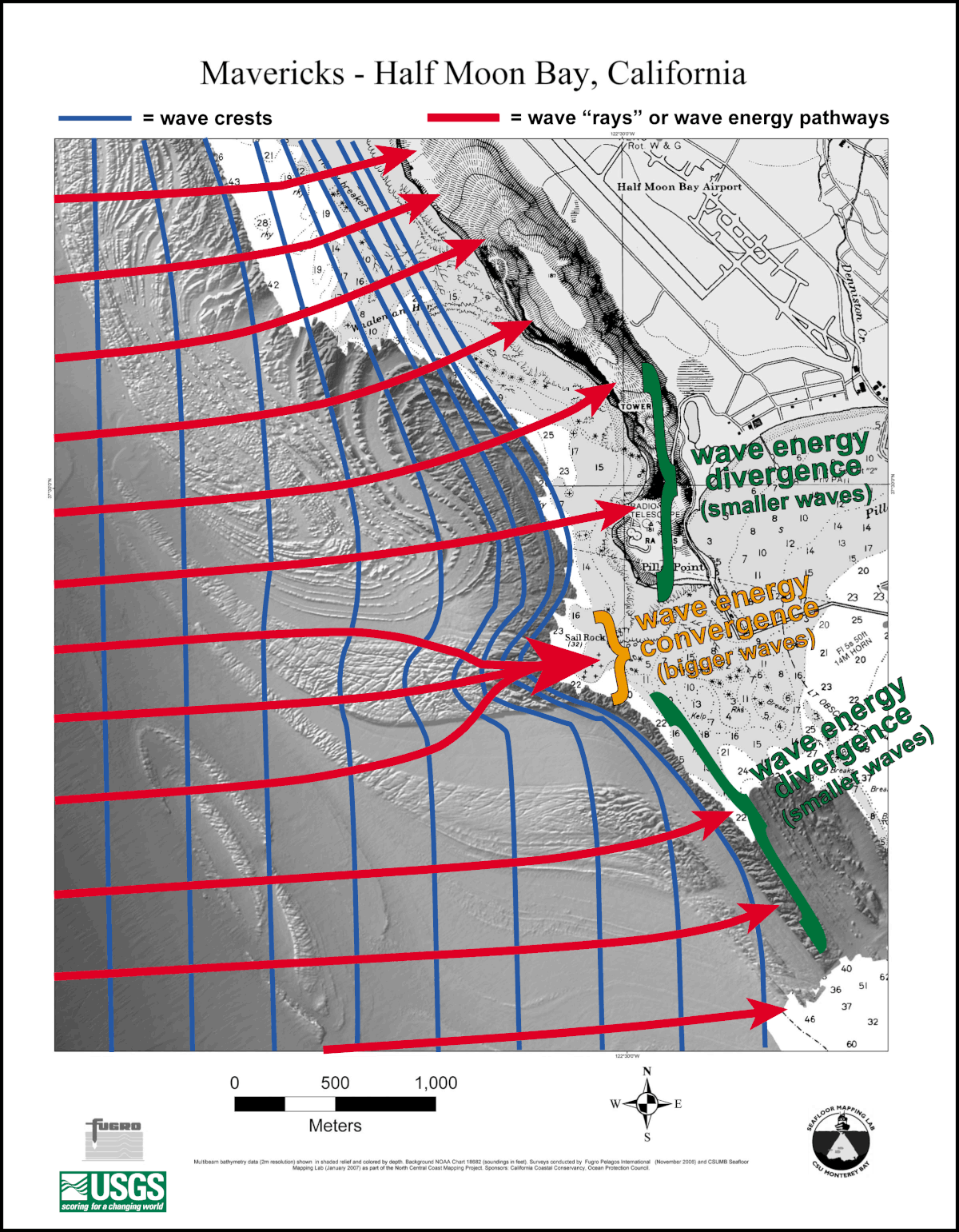
波線の収束(幅の縮小 b { b}
)
カリフォルニア州マーベリックスで、高いサーフィン波を生み出して
います。赤い線は波の光線です。青い線は
波面です。隣接する波の光線間の距離は
、深浅測量による
屈折(深さの変化)のために海岸に向かって変化します。波面間の距離は、
波の浅瀬(深さの減少)
のために海岸に向かって減少します h { h}
)。
線形化された 浅水方程式に基づくこの法則によれば、波高の空間的変動 H { H}
(振幅の2倍 a { a}
正弦波の場合、孤立波の振幅に等しい)平均深度の水中を進行波の場合 h { h}
と幅 b { b}
(開水路の場合) を満たすH b h
4 = 絶え間ない { H 、{ sqrt {b}} 、{ sqrt {h}} = { text {constant}}、}
どこh 4
{ { sqrt {h}}}
の4番目のルートです
h {h。}
したがって、1と2のラベルが付いた開水路の2つの断面を考慮すると、セクション2の波高は次のようになります。H 2 = b 1 b 2h 1 h2 H
1 { H_ {2} = { sqrt { frac {b_ {1}} {b_ {2}}}} ; { sqrt { frac {h_ {1}} {h_ { 2}}}} ; H_ {1}、}
下付き文字1および2は、関連する断面の数量を示します。したがって、深さが16分の1に減少すると、波は2倍の高さになります。そして、チャネル幅が徐々に4分の1に減少した後、波高は2倍になります。海岸線に平行な深さの等高線を持つまっすぐな海岸に向かって垂直な波の伝播にb
{ b}
定数、たとえば1メートルまたはヤード。
海や海岸近くで長波を屈折させるための幅 b { b}
波の光線間の距離として解釈することができます。光線(および光線間の間隔の変化)は、幾何光学近似から線形波の伝播まで続きます。真っ直ぐな平行な深さの等高線の場合、これはスネルの法則の使用を単純化します。
グリーンは1838年に彼の結果を発表しました 。これは現在WKB近似として知られている方法に進化する方法–リウヴィル–グリーン法–に基づいています。グリーンの法則は、長波の平均水平波エネルギーフラックスの不変性にも対応しています。 b g h1 8 ρ g H 2 = 絶え間ない { b 、{ sqrt {gh}} 、{ tfrac {1} {8}} rho gH ^ {2} = { text {constant}}、}
どこg h
{ { sqrt {gh}}}
群速度(浅瀬での位相速度に等しい)、1 8ρ g
H2 1 2ρ g a 2
{ { tfrac {1} {8}} rho gH ^ {2} = { tfrac {1} {2}} rho ga ^ {2}}
は、深さ全体および水平面積の単位あたりに統合された平均波エネルギー密度です。 g { g}
は重力加速度であり、 ρ { rho}
は水の密度です。
波長と周期
さらに、グリーンの分析から、波長 λ { lambda}
浅瀬への浅瀬での波の長さは短くなり、 λ g h =
絶え間ない
{ { frac { lambda} { sqrt {g 、h}}} = { text {constant}}}
波に沿って。グリーンの線形理論によれば、浅瀬波の振動周期(したがって周波数も)は変化しません。
導出
グリーンは、水深の段階的な変化に適用できる、現在リウビル-グリーン法として知られている方法を使用して、水の波に対する彼の浅瀬の法則を導き出しました。 h { h}
と幅 b { b}
波の伝播の経路に沿って。
開水路の波動方程式
開始点は、長方形の断面(垂直の側壁)を持つ開水路の線形化された1次元のSaint-Venant方程式です。これらの方程式は、自由表面の標高を持つ波の進化を表しています η (( X t )。 { eta(x、t)}
および水平流速 u (( X t
)。 { u(x、t)、}
とX
{ x}
チャネル軸に沿った水平座標と t { t}
時間: b ∂ η ∂t + ∂(( bh u
)。∂X =
0 ∂u ∂ t + g
∂η X =
0 { { begin {aligned}&b 、{ frac { partial eta} { partial t}} + { frac { partial(b 、h 、u)} { partial x}} = 0、\&{ frac { partial u} { partial t}} + g 、{ frac { partial eta} { partial x}} = 0、 end {aligned}}}
どこ g { g}
は地球の重力(定数と見なされます)、 h { h}
は平均水深であり、 b { b}
はチャネル幅であり、∂ / ∂ t
{ partial / partial t}
と∂ / ∂X
{ partial / partial x}
は、空間と時間に関する偏導関数を示しています。幅のゆっくりとした変化 b { b}
と深さ h { h}
距離でX
{ x}
チャネル軸に沿って、次のように表すことで考慮されます。 b (( μX )。 { b( mu x)}
と h (( μX
)。 { h( mu x)、}
どこ μ { mu}
は小さなパラメータです:μ ≪
1.1。
{ mu ll 1.}
上記の2つの方程式は、表面標高の1つの波動方程式に組み合わせることができます。
∂2 ∂ t 2 − g b ∂ ∂X (( b h ∂
X)。 = 0 { { frac { partial ^ {2} eta} { partial t ^ {2}}}-{ frac {g} {b}} 、{ frac { partial} { partial x }} left(b 、h 、{ frac { partial eta} { partial x}} right)= 0、}
と次の速度でu = − g ∫ ∂ η∂X d
t { u = -g int { frac { partial eta} { partial x}} ; mathrm{d}t。}
(1) Liouville–Green法では、アプローチは、不均一な係数を持つ上記の波動方程式を均一なものに変換することです( μ
{ mu}
)。
独立変数としての波動位相への変換
次のステップは、座標変換を適用して、移動時間(または波の位相)を導入することです。 τ { tau}
によって与えられたdX d τ = g
h { { frac { mathrm {d} x} { mathrm {d} tau}} = { sqrt {g 、h}}、}
それで
τ = ∫X 0X1 h(( μ s )。 d s
{ tau = int _ {x_ {0}} ^ {x} { frac {1} { sqrt {g 、h( mu s)}}} ; mathrm {d} s}
とX { x}
セレリティを通じて関連しているc = g
h { c = {sqrt{gh}}。}
スロー変数の紹介X= μX
{ X = mu x}
およびの導関数を示す b (( X )。 { b(X)}
と h (( X )。 { h(X)}
に関してX
{ X}
プライムで、例えばb ′ = d b /
dX { b’= mathrm {d} b / mathrm {d} X、}
theX { x}
-波動方程式の導関数、式。(1)、になる:∂ η X =(( dXd τ
)。 1∂ η ∂ τ 1g h ∂ η
∂τ と
∂ ∂X (( bh ∂ η ∂X
)。= b
h∂ 2
η + μ(( b ′ h+ b h
′)。∂ η X = b g ∂ 2 η 2+ μ b ′ h+1 2 ′ g h ∂ η ∂ τ { { begin {aligned}&{ frac { partial eta} { partial x}} = left({ frac { mathrm {d} x} { mathrm {d} tau}} right)^ {-1} 、{ frac { partial eta} { partial tau}} = { frac {1} { sqrt {g 、h}}} 、{ frac { partial eta} { partial tau}} qquad { text {and}} \&{ frac { partial} { partial x}} left(b 、h 、{ frac { partial eta} { partial x}} right)= b 、h 、{ frac { partial ^ {2} eta} { partial x ^ {2}}} + mu left( b’、h + b 、h’ right)、{ frac { partial eta} { partial x}} = { frac {b} {g}} 、{ frac { partial ^ {2} eta} { partial tau ^ {2}}} + mu 、{ frac {b’、h + { tfrac {1} {2}} 、b 、h’} { sqrt {gh}}} 、{ frac { partial eta} { partialtau}}。end{aligned}}}
ここで、波動方程式(1)は次のように変換されます。
∂2 ∂ t 2 −
∂2 ∂ τ 2 − μ
g h (( b′ b+1 2h ′ h
)。∂ η ∂ τ = 0。
{ { frac { partial ^ {2} eta} { partial t ^ {2}}}-{ frac { partial ^ {2} eta} { partial tau ^ {2}} }- mu 、{ sqrt {g 、h}} 、 left({ frac {b’} {b}} + { tfrac {1} {2}} 、{ frac {h ‘} {h}} right)、{ frac { partial eta} { partial tau}}=0。}
(2) 次のステップは、近似の2次の均一性からの偏差のみが残るように、つまりに比例するように方程式を変換することです。 μ 2 { mu^{2}。}
均質性へのさらなる変革
均一波動方程式(すなわち、方程式(2) μ { mu}
ゼロです)解決策がありますη = F(( t± τ )。 { eta = F(t pm tau)}
負または正のいずれかで伝播する永続的な形の進行波の場合X
{ x}
-方向。不均一な場合、正の波が伝播することを考慮しますX
{ x}
-方向、グリーンはおおよその解決策を提案します: η (( τ t
)。= Θ(( X
)。 F (( t− τ
)。 { eta( tau、t)= Theta(X)、F(t- tau)。}
(3) それで∂ 2
η = Θ d
2F d τ 2∂ η
∂τ = Θ d F d τ+μ g h Θ ′ F
と∂ 2
η 2= Θ d
2F d τ 2+2 g h Θ ′ d F d τ +μ 2 g ″
F { { begin {aligned} { frac { partial ^ {2} eta} { partial t ^ {2}}}&= Theta 、{ frac { mathrm {d} ^ {2 } F} { mathrm {d} tau ^ {2}}}、\ { frac { partial eta} { partial tau}}&= Theta 、{ frac { mathrm {d } F} { mathrm {d} tau}} + mu 、{ sqrt {g 、h}} 、 Theta’、F qquad { text {and}} \ { frac { partial ^ {2} eta} { partial tau ^ {2}}}&= Theta 、{ frac { mathrm {d} ^ {2} F} { mathrm {d} tau ^ {2}}} + 2 、 mu 、{ sqrt {g 、h}} 、 Theta’、{ frac { mathrm {d} F} { mathrm {d} tau }} + mu ^ {2} 、g 、h 、 Theta” 、F。 end {aligned}}}
ここで、式の左辺。(2)は次のようになります。μ g h(( 2Θ ′ Θ + b ′
b 1 2h ′ h )。 Θd F d τ + μ 2g h (( Θ″ Θ ′ + b ′
b 1 2h ′ h
)。 Θ ′
F { mu 、{ sqrt {g 、h}} 、 left(2 、{ frac { Theta’} { Theta}} + { frac {b’} {b}} + { tfrac {1} {2}} 、{ frac {h’} {h}} right)、 Theta 、{ frac { mathrm {d} F} { mathrm {d} tau}} + mu ^ {2} 、g 、h 、 left({ frac { Theta”} { Theta’}} + { frac {b’} {b}} + { tfrac {1} {2}} 、{ frac {h’} {h}} right)、 Theta’ 、F。}
したがって、式(1)で提案されたソリューション。(3)は式を満たします。(2)、したがって、式も。(1)上記の2つの項は別として μ { mu}
とμ 2
{ mu ^ {2}}
、 とμ ≪
1.1。
{ mu ll 1.}
ソリューションのエラーは順序どおりに作成できます O (( μ
2)。
{ { mathcal {O}}( mu ^ {2})}
提供された2 Θ ′ Θ + b ′ b +1 2h ′ h = 0。
{ 2 、{ frac { Theta’} { Theta}} + { frac {b’} {b}} + { tfrac {1} {2}} 、{ frac {h ‘ } {h}}=0。}
これには解決策があります: Θ (( X
)。= α b
−1 2h − 1
4 { Theta(X)= alpha 、b ^ {-{ tfrac {1} {2}}} 、h ^ {-{ tfrac{1}{4}}}。}
式を使用して。(3)とからの変換X
{ x}
に τ { tau}
、表面標高の近似解 η (( X t )。 { eta(x、t)}
は η (( X t
)。= b
−1 2(( X
)。 h −1 4(( X
)。 F (( t− X 0X 1 g h (( s
)。 d s)。+ O(( μ
2)。 { eta(x、t)= b ^ {-{ tfrac {1} {2}}}(x); h ^ {-{ tfrac {1} {4}}}(x) ; F left(t- int _ {x_ {0}} ^ {x} { frac {1} { sqrt {g 、h(s)}}} ; mathrm {d} s right )+ { mathcal {O}}( mu ^ {2})、}
(4) ここで、定数 α { alpha}
一般性を失うことなく、1に設定されています。ネガティブに伝わる波X
{ x}
-方向の関数の引数にマイナス記号があります F { F}
プラス記号に反転します。理論は線形であるため、重ね合わせの原理により解を追加できます。
正弦波とグリーンの法則
時間とともに正弦波に変化する波
T { T、}