ホフスタッターの蝶

Hofstadter’s_butterfly
物性物理学では、ホフスタッターの蝶は、格子内の垂直磁場内の相互作用しない2次元電子のスペクトル特性のグラフです。スペクトルのフラクタルで自己相似性は1976年の博士号で発見されました。ダグラスホフスタッターの作品であり、現代の科学データの視覚化の初期の例の1つです。この名前は、ホフスタッターが書いたように、「大きなギャップが蝶に似た非常に印象的なパターンを形成している」という事実を反映しています。
Hofstadterによる蝶のレンダリング
ホフスタッターの蝶は、整数量子ホール効果の理論とトポロジカル量子数の理論で重要な役割を果たします。

コンテンツ
1 歴史
1.1 確認
2 理論モデル
2.1 ハーパーの方程式とワニエ処理の解 2.2 状態図、コンダクタンス、トポロジー
3 参考文献

歴史
垂直な均​​一磁場が作用する2D格子上の電子の最初の数学的記述は、1950年代にルドルフパイエルスと彼の学生であるRGハーパーによって研究されました。
Hofstadterは、1976年に、垂直磁場におけるブロッホ電子のエネルギー準位に関する記事でこの構造を最初に説明しました。さまざまな周波数でのハーパーの方程式のスペクトルをグラフで表したものです。このスペクトルの数学的構造の重要な側面の1つである、磁場の特定の値に対するエネルギーバンドの単一次元（エネルギー）に沿った分割は、1964年にソビエトの物理学者Mark Azbelが通過したときに以前に言及されていました（ホフスタッターが引用した論文で）、しかしホフスタッターはすべてのエネルギー値に対して磁場のすべての値をプロットすることによってその作業を大幅に拡張し、スペクトルのユニークな再帰的幾何学的特性を最初に明らかにした2次元プロットを作成しました。
ホフスタッターがオレゴン大学に在籍していたときに書かれた彼の論文は、さらなる研究を指揮する上で影響力を持っていました。理論的根拠に基づいて、2次元正方格子内の電子の許容エネルギー準位値が、システムに垂直に印加された磁場の関数として、現在フラクタルセットとして知られているものを形成すると予測しました。つまり、印加磁場の小規模な変化に対するエネルギー準位の分布は、大規模な構造で見られるパターンを再帰的に繰り返します。 Hofstadterが図と呼んだように、「Gplot」は、ブノワ・マンデルブロの新しく造られた単語「フラクタル」が英語のテキストで紹介される前に書かれた、PhysicalReviewBの1976年の記事で再帰構造として説明されました。ホフスタッターはまた、1979年の著書ゲーデル、エッシャー、バッハでこの人物について論じています。この構造は、一般に「ホフスタッターの蝶」として知られるようになりました。
David J. Thoulessと彼のチームは、蝶の羽がChern整数によって特徴付けられることを発見しました。これは、Hofstadterのモデルでホールコンダクタンスを計算する方法を提供します。

確認

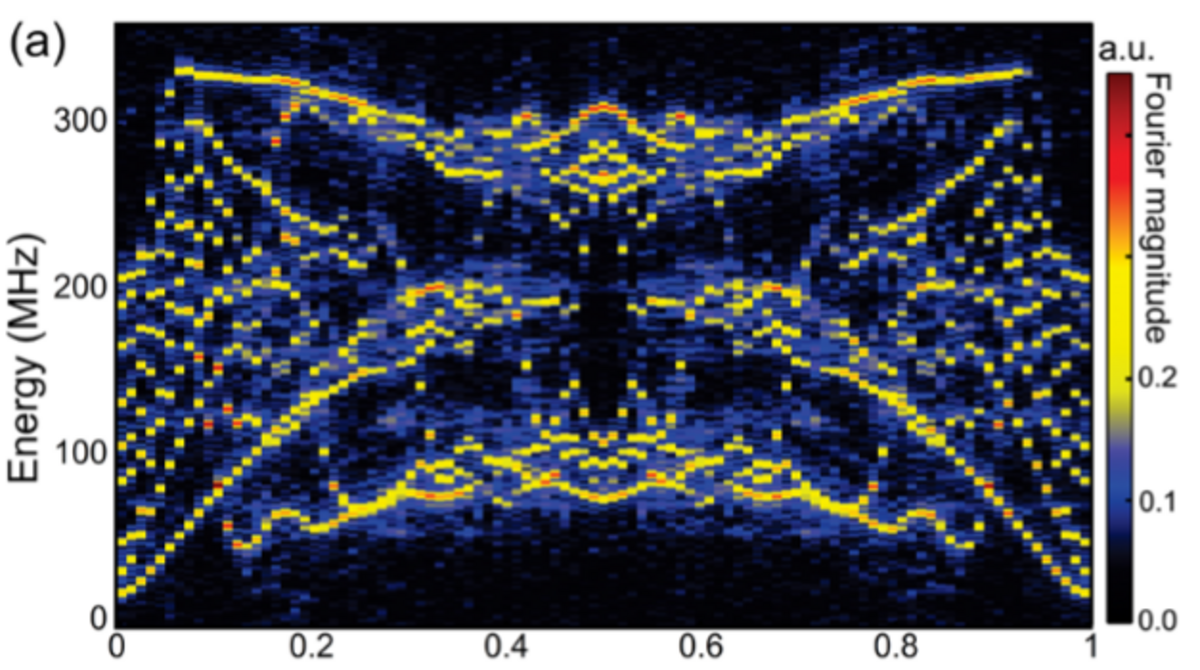
  超伝導量子ビットを介した電子のシミュレーションにより、ホフスタッターの蝶が得られます
1997年、ホフスタッターの蝶は、一連の散乱体を備えたマイクロ波ガイドを使った実験で再現されました。散乱体を備えたマイクロ波ガイドの数学的記述と磁場中のブロッホの波との類似性により、散乱体の周期列に対するホフスタッターの蝶の再現が可能になりました。
2001年、Christian Albrecht、Klaus von Klitzingとその同僚は、Thoulessetalをテストするための実験的なセットアップを実現しました。超格子ポテンシャルに二次元電子ガスがあるホフスタッターの蝶についてのの予測。
2013年に、3つの別々の研究者グループが、六方晶窒化ホウ素基板上に製造されたグラフェンデバイスにおけるホフスタッターの蝶のスペクトルの証拠を独自に報告しました。 この場合、バタフライスペクトルは、印加された磁場と、グラフェン格子が窒化ホウ素とほぼゼロの角度の不一致で配向したときに発生する大規模なモアレパターンとの相互作用から生じます。
2017年9月、Googleのジョンマルティニスのグループは、CQTシンガポールのアンジェラキスグループと協力して、9つの超伝導キュビットの相互作用する光子を使用した垂直磁場内の2D電子のシミュレーションの結果を公開しました。シミュレーションでは、予想どおり、ホフスタッターの蝶が回復しました。

理論モデル

  ホフスタッターの蝶は、エネルギー比がハーパーの方程式のグラフィカルなソリューションです。 ϵ { epsilon}

 フラックス比の関数としてプロットされます2 π α { 2 pi alpha}

 。
彼の元の論文で、ホフシュタッターは次の導出を検討しています。格子間隔のある2次元正方格子内の荷電量子粒子 a { a}

 は、単一のブロッホバンドに制限された垂直な静的均一磁場の下で、周期的なシュレディンガー方程式によって記述されます。2D正方格子の場合、強結合エネルギー分散関係は次のようになります。 W （（ k）。= E 0（（ coskX a + cos k y a
）。= E0 （（ eI X
a+ e − I X
a+ e I
k y a+ e − I
k y a ）。 { W（ mathbf {k}）= E_ {0}（ cos k_ {x} a + cos k_ {y} a）= { frac {E_ {0}} {2}}（e ^ { ik_ {x} a} + e ^ {-ik_ {x} a} + e ^ {ik_ {y} a} + e ^ {-ik_ {y} a}）}

 、
どこ W （（ k ）。 { W（ mathbf {k}）}

 はエネルギー関数です、k =（（ kX k
y）。
{ mathbf {k} =（k_ {x}、k_ {y}）}

 は結晶運動量であり、E 0
{ E_ {0}}

 経験的パラメータです。磁場B = ∇
×× A { mathbf {B} = nabla times mathbf {A}}

 、 どこ A { mathbf{A}}

 磁気ベクトルポテンシャルは、パイエルス置換を使用して、結晶運動量を正準運動量に置き換えることで考慮に入れることができます。ℏ k p − q A
{ hbar mathbf {k} to mathbf {p} -q mathbf {A}}

 、 どこp =（（ pX p
y）。
{ mathbf {p} =（p_ {x}、p_ {y}）}

 は粒子の運動量演算子であり、 q { q}

 は粒子の電荷です（ q= − e
{ q = -e}

 電子のために、 e { e}

 電気素量です）。便宜上、ゲージを選択しますA =（（ 0 BX 0 ）。 { mathbf {A} =（0、Bx、0）}

 。
それを使用してe I p
j a { e ^ {ip_ {j} a}}

 は並進演算子なので、e I p
j a ψ（（ X y
）。= ψ（（ X+ a y ）。 { e ^ {ip_ {j} a} psi（x、y）= psi（x + a、y）}

 、 どこ j =X y z
{ j = x、y、z}

 と ψ （（ r
）。= ψ（（ X y ）。 { psi（ mathbf {r}）= psi（x、y）}

 は粒子の2次元波動関数です。使用できます W （（ p− q A ）。 { W（ mathbf {p} -q mathbf {A}）}

 次の時間に依存しないシュレディンガー方程式を取得するための効果的なハミルトニアンとして：E ψ（（ X y
）。= E0
[ ψ（（ X+ a y
）。+ ψ（（ X− a y
）。+ ψ（（ X y+ a ）。 e − Iq BX a / ℏ + ψ（（ X y− a ）。 e+ I q BX a /
ℏ] { E psi（x、y）= { frac {E_ {0}} {2}} left [ psi（x + a、y）+ psi（xa、y）+ psi（x 、y + a）e ^ {-iqBxa / hbar} + psi（x、ya）e ^ {+ iqBxa / hbar}right]。}
  粒子は格子内の点間でしかホップできないことを考慮して、次のように記述します。X= n a y = m a
{ x = na、y = ma}

 、 どこ n m { n、m}

 整数です。Hofstadterは次の仮説を立てます： ψ （（ X y
）。= g n e I ν m { psi（x、y）= g_ {n} e ^ {i nu m}}

 、 どこ ν { nu}

 ハーパーの方程式（概マシュー作用素としても知られています）を得るために、エネルギーに依存しますλ = 1
{ lambda = 1}

 ）：g n + 1 + g n− 1 + 2 cos（（ 2π n α − ν
）。g n = ϵ g
n { g_ {n + 1} + g_ {n-1} +2 cos（2 pi n alpha- nu）g_ {n} = epsilon g_ {n}、}
  どこϵ = 2 E / 0 { epsilon = 2E / E_ {0}}

 とα = ϕ（（ B ）。 / 0
{ alpha = phi（B）/ phi _ {0}}

 、 ϕ （（ B
）。= B a 2
{ phi（B）= Ba ^ {2}}

 は格子セルを通る磁束に比例し、
ϕ0 2π ℏ / q
{ phi _ {0} = 2 pi hbar / q}

 は磁束量子です。フラックス比 α { alpha}

 磁気長で表すこともできますl m = ℏ /e B { textstyle l _ { rm {m}} = { sqrt { hbar / eB}}}

 、 そのようなα =（（ 2 π ）。 − 1（（ a / l
m）。 2 { textstyle alpha =（2 pi）^ {-1}（a / l _ { rm {m}}）^ {2}}

 。
ホフスタッターの蝶は、ϵ α
{ epsilon _ { alpha}}

 磁束比の関数として α { alpha}

 、 どこϵ α
{ epsilon _ { alpha}}

 可能なすべてのセットです ϵ { epsilon}

 これはハーパーの方程式の解です。

ハーパーの方程式とワニエ処理の解

  ゼロ温度でのホフスタッターの蝶の状態図。横軸は左から電子がないところから始まる電子密度を示しています。縦軸は磁束の強さを示しており、下部のゼロから始まり、より高い磁場に対してパターンが周期的に繰り返されます。色は、TKNN（Thouless、Kohmoto、Nightingale、Nijs）整数としても知られる、スペクトルのギャップのチャーン数を表します。青みがかった冷たい色は負のチャーン数を示し、暖かい赤は正のチャーン数を示し、白はゼロを示します。
余弦関数の特性により、パターンは周期的です。 α { alpha}

 周期1（単位セルあたりの量子フラックスごとに繰り返されます）。の領域のグラフ α { alpha}

 0と1の間では、線対称性があります α =1 2
{ textstyle alpha = { frac {1} {2}}}

 とϵ = 0
{ epsilon = 0}

 。注意してください ϵ { epsilon}

 必然的に-4と4の間に制限されます。
ハーパーの方程式には、解が次の合理性に依存するという特定の特性が α { alpha}

 。周期性を課すことによって n { n}

 、次の場合にそれを示すことができますα = P / Q
{ alpha = P / Q}

 （有理数）、ここで P { P}

 と Q { Q}

 明確な素数であり、正確にあります Q { Q}

 エネルギーバンド。大用Q ≫ P
{ Q gg P}

 、エネルギーバンドはランダウ準位に対応する薄いエネルギーバンドに収束します。
グレゴリー・ワニエは、状態密度を考慮に入れることにより、システムを説明するディオファントス方程式を得ることができることを示しました。
n 0 S + T α
{ { frac {n} {n_ {0}}} = S + T alpha}
  どこn =
∫ 4ϵ F ρ（（ ϵ
）。 d ϵ; n 0 =
∫ 4 4 ρ （（ ϵ
）。 d ϵ
{ n = int _ {-4} ^ { epsilon _ { rm {F}}} rho（ epsilon） mathrm {d} epsilon ;; ; n_ {0} = int _ {-4} ^ {4} rho（ epsilon） mathrm {d} epsilon}
  どこ S { S}

 と T { T}

 は整数であり、 ρ （（ ϵ ）。 { rho（ epsilon）}

 は、与えられた状態密度です α { alpha}

 。ここ n { n}

 フェルミエネルギーまでの状態の数を数え、n 0
{ n_ {0}}

 完全に満たされたバンドのレベルに対応します（からϵ = − 4
{ epsilon =-4}

 にϵ = 4
{ epsilon = 4}

 ）。この方程式は、ハーパーの方程式のすべての解を特徴づけます。最も重要なことは、 α { alpha}

 は無理数であり、のための解決策は無限にありますϵ α
{ epsilon _ { alpha}}

 。
すべての組合ϵ α
{ epsilon _ { alpha}}

 の有理数と非有理数の間で不連続な自己相似フラクタルを形成します α { alpha}

 。この不連続性は非物理的であり、連続性は有限の不確実性のために回復されます B { B}

 または有限サイズの格子の場合。実際の実験で蝶を解像できるスケールは、システムの特定の条件によって異なります。

状態図、コンダクタンス、トポロジー
垂直磁場、化学ポテンシャル、温度の関数としての2次元正方格子内の電子の状態図には、無限に多くの相がThoulessと同僚は、各フェーズがすべての整数値が許可される積分ホールコンダクタンスによって特徴付けられることを示しました。これらの整数は、チャーン数として知られています。

参考文献
^ k l Hofstadter、Douglas R.（1976）。「合理的および非合理的な磁場におけるブロッホ電子のエネルギー準位と波動関数」。フィジカルレビューB。14（6）：2239–2249。Bibcode：1976PhRvB..14.2239H。土井：10.1103/PhysRevB.14.2239。
^ Avron J、Osadchy D.、およびSeiler R.（2003）。「量子ホール効果のトポロジー的考察」。今日の物理学。53：38。doi：10.1063/1.1611351。
^ ハーパー、PG（1955）。「準周期性システムのスケーリング分析：一般化されたハーパーモデル」。物理学会の議事録。68：874。
^ アズベル’、マークヤ。（1964）。「磁場中の伝導電子のエネルギースペクトル」。Journal of Experimental andTheoreticalPhysics。19（3）：634–645。
^ Thouless D.、Kohmoto M、NightngaleおよびM. den-Nijs（1982）。「二次元周期ポテンシャルにおける量子化ホールコンダクタンス」。物理的レビューレター。49（6）：405–408。Bibcode：1982PhRvL..49..405T。土井：10.1103/PhysRevLett.49.405。
^ Kuhl、U .; Stöckmann、H.-J。（1998年4月13日）。「ホフスタッターの蝶のマイクロ波実現」。物理的レビューレター。80（15）：3232–3235。Bibcode：1998PhRvL..80.3232K。土井：10.1103/PhysRevLett.80.3232。
^ Albrecht、C .; スメット、JH; von Klitzing、K .; ワイス、D .; Umansky、V .; Schweizer、H.（2001-01-01）。「量子化されたホールコンダクタンスにおけるホフスタッターのフラクタルエネルギースペクトルの証拠」。物理的レビューレター。86（1）：147–150。土井：10.1103/PhysRevLett.86.147。ISSN0031-9007。_   ^ ディーン、CR; 王、L .; Maher、P .; フォーサイス、C .; ガハリ、F .; Gao、Y .; Katoch、J .; 石神正明; 月、P .; 越野正明; 谷口徹; 渡辺健一; シェパード、KL; ホーン、J .; キム、P。（2013年5月30日）。「ホフスタッターの蝶とモアレ超格子におけるフラクタル量子ホール効果」。自然。497（7451）：598–602。arXiv：1212.4783。Bibcode：2013Natur.497..598D。土井：10.1038/nature12186。PMID23676673。_   ^ ポノマレンコ、LA; ゴルバチョフ、RV; ユウ、GL; エリアス、DC; ジャリル、R .; パテル、AA; Mishchenko、A .; マヨロフ、AS; ウッズ、CR; ウォールバンク、JR; Mucha-Kruczynski、M .; ピオ、BA; ポテムスキー、M .; グリゴリエバ、IV; ノボセロフ、KS; ギニア、F .; ファルコ、VI; Geim、AK（2013年5月30日）。「グラフェン超格子におけるディラックフェルミオンのクローニング」。自然。497（7451）：594–597。arXiv：1212.5012。Bibcode：2013Natur.497..594P。土井：10.1038/nature12187。hdl：10261/93894。PMID23676678。_   ^ ハント、B .; Sanchez-Yamagishi、JD; 若い、AF; Yankowitz、M .; LeRoy、BJ; 渡辺健一; 谷口徹; 月、P .; 越野正明; Jarillo-Herrero、P .; アシュオリ、RC（2013）。「ファンデルワールスヘテロ構造における大規模なディラックフェルミオンとホフスタッターの蝶」。科学。340（6139）：1427–1430。arXiv：1303.6942。Bibcode：2013Sci…340.1427H。土井：10.1126/science.1237240。PMID23686343。_   ^ Roushan、P .; ニール、C .; タンパニタノン、J .; バスティダス、VM; Megrant、A .; Barends、R .; チェン、Y .; Chen、Z .; Chiaro、B .; ダンズワース、A .; ファウラー、A .; Foxen、B .; ジュスティーナ、M .; ジェフリー、E .; ケリー、J .; ルセロ、E .; Mutus、J .; ニーリー、M .; キンタナ、C .; サンク、D .; Vainsencher、A .; ウェナー、J .; ホワイト、T .; Neven、H .; アンジェラキス、DG; Martinis、J.（2017-12-01）。「超伝導キュビットにおける相互作用する光子による局在化の分光学的特徴」[相互作用する光子による多体局在化の分光学的特徴]。科学。358（6367）：1175–1179。arXiv：1709.07108。土井：10.1126/science.aao1401。ISSN0036-8075。_ PMID29191906。_    ^ ワニエ、GH（1978-08-01）。「磁場中のブロッホ電子の合理性に依存しない結果」。フィジカステータスソリディB。88（2）：757–765。土井：10.1002/pssb.2220880243。
^ アナリティス、ジェームズG .; ブランデル、スティーブンJ .; Ardavan、Arzhang。「ランダウ準位、分子軌道、および有限系におけるホフスタッターの蝶」。American JournalofPhysics。72（5）：613–618。土井：10.1119/1.1615568。ISSN0002-9505。_  “