Mean_absolute_error
平均絶対偏差または平均絶対差 と混同しないで
統計では、平均絶対誤差( MAE ) は、同じ現象を表す対になった観測値間の誤差の尺度です。Y対Xの例には、予測対観測、後続時間対初期時間、および 1 つの測定技術と別の測定技術の比較が含まれます。MAE は、絶対誤差の合計をサンプル サイズで割った値として計算されます: M あ え = ∑ I =1
| |y I −X I
| |n = ∑ I =1
| |
e I | |n .
{ mathrm {MAE} ={frac {sum _{i=1}^{n}left|y_{i}-x_{i}right|}{n}}={frac { sum _{i=1}^{n}left|e_{i}right|}{n}}.}
したがって、絶対誤差の算術平均です
| |e I
| | = | |y I −X I
| |
{ |e_{i}|=|y_{i}-x_{i}|}
、 どこy I
{ y_{i}}
は予測であり、X I { x_{i}}
真の価値。別の定式化では、重み係数として相対度数を含めることができることに注意して平均絶対誤差は、測定されるデータと同じスケールを使用します。これはスケール依存の精度尺度として知られているため、異なるスケールを使用するシリーズ間の比較には使用できません。平均絶対誤差は、時系列分析における予測誤差の一般的な尺度であり、平均絶対偏差のより標準的な定義と混同して使用されることが同じ混乱がより一般的に存在します。
コンテンツ
1 数量の不一致と割り当ての不一致
2 関連する措置
2.1 最適性プロパティ
2.1.1 最適性の証明
3 こちらもご覧ください
4 参考文献
数量の不一致と割り当ての不一致
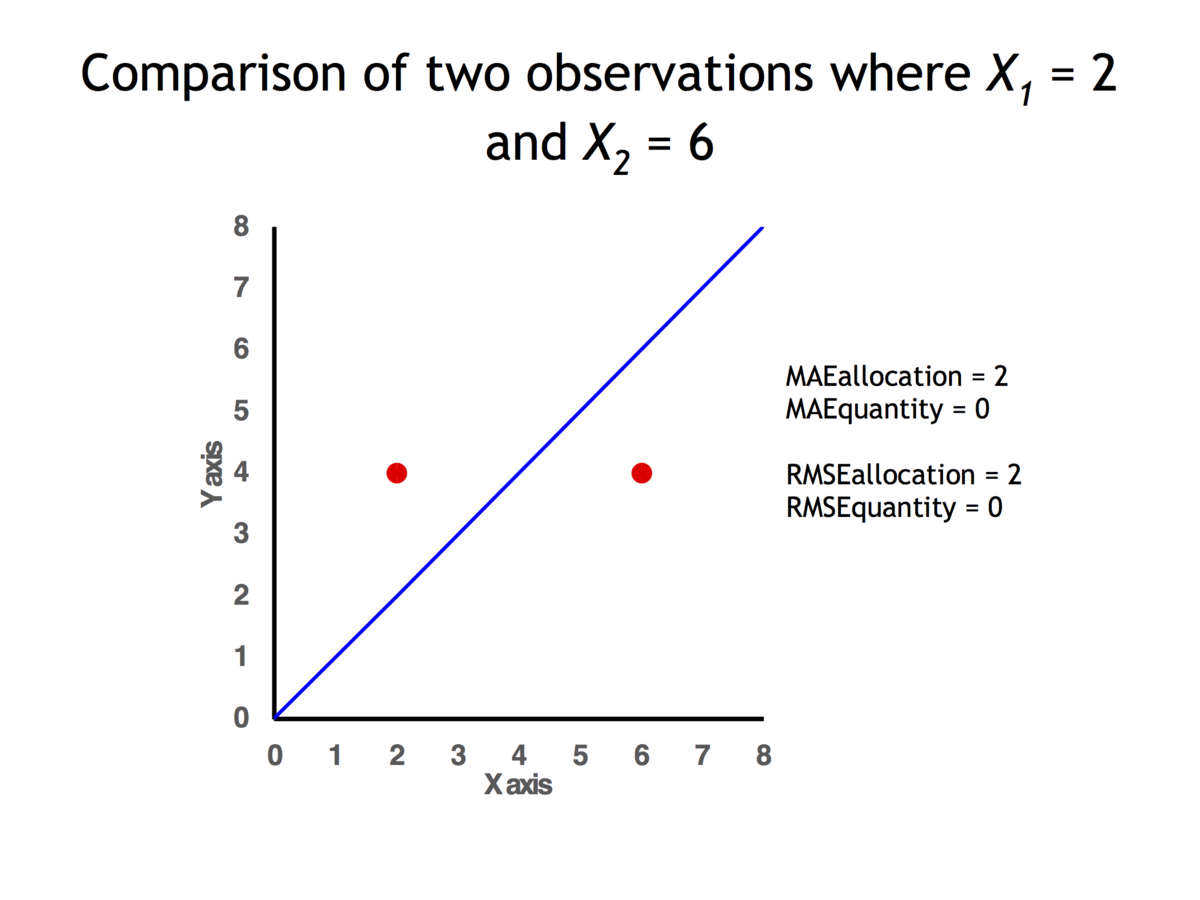
MAE と RMSE の両方で、Quantity Disagreement が 0 で、Allocation Disagreement が 2 である 2 つのデータ ポイント
MAE は、数量の不一致と割り当ての不一致という 2 つのコンポーネントの合計として表すことができます。量の不一致は、以下によって与えられる平均誤差の絶対値です: M え = ∑ I =1 y I −X In .
{ mathrm {ME} ={frac {sum _{i=1}^{n}y_{i}-x_{i}}{n}}.}
割り当ての不一致は、MAE から数量の不一致を差し引いたものです。
また、(X y ) { (x,y)}
プロット。X 値の平均が Y 値の平均と等しくない場合、数量の差異が存在します。ポイントがアイデンティティ ラインの両側に存在する場合にのみ、割り当ての違いが存在します。
関連する措置
平均絶対誤差は、予測を最終的な結果と比較する多くの方法の 1 つです。確立された代替手段は、平均絶対スケール誤差(MASE) と平均二乗誤差です。これらはすべて、過大予測または過小予測の方向を無視する方法でパフォーマンスを要約しています。これを強調する指標は平均符号差です。
最小二乗アプローチが平均二乗誤差に関連するという意味で、選択されたパフォーマンス メジャーを使用して予測モデルを適合させる場合、平均絶対誤差に相当するものは最小絶対偏差です。
MAE は二乗平均平方根誤差(RMSE) と同じではありませんが、一部の研究者はそのように報告して解釈しています。MAE は RMSE よりも概念的に単純で、解釈も容易です。これは、散布図の各点と Y=X 線との間の垂直または水平の絶対絶対距離の平均です。言い換えると、MAE は X と Y の間の平均絶対差です。さらに、各エラーは、エラーの絶対値に比例して MAE に寄与します。これは、差を 2 乗することを含む RMSE とは対照的であるため、いくつかの大きな差によって RMSE が MAE よりも大幅に増加します。これらの違いについては、上記の例を参照して
最適性プロパティ
確率変数Xに関する実変数cの平均絶対誤差は次のとおりです。 え ( | |X− c
| | ) { E(left|Xcright|)}
Xの確率分布が上記の期待値が存在するようなものであるとすると、mがXに関する平均絶対誤差の最小化である場合に限り、mはXの中央値になります。特に、mが絶対偏差の算術平均を最小化する場合に限り、m は標本中央値です。
より一般的には、中央値は最小値として定義されます。 え ( | |X− c
| | − | |X
| |
){ E(|Xc|-|X|),}
多変量中央値で説明されているように(具体的には空間中央値で)。
中央値のこの最適化ベースの定義は、統計データ分析 (たとえば、k中央値クラスタリング) で役立ちます。
最適性の証明
ステートメント: 最小化する分類子 え | |y − y
^ | |
{ mathbb {E} |y-{hat {y}}|}
は へ
^ (X) =
中央値 ( y | |X=X )
{ {hat {f}}(x)={text{中央値}}(y|X=x)}
. 証拠:
分類の損失関数は次のとおりです。 L [| |y − a
| |
| |X= x ] =
∫− ∞ ∞ | y − a Y |X y ) d y =
∫− ∞ a a − y )
fY | X y ) d y +
∫a ∞ y − a )
fY | X y ) d y
{ {begin{aligned}L&=mathbb {E} \&=int _{-infty }^{infty }|ya|f_{Y|X }(y),dy\&=int _{-infty }^{a}(ay)f_{Y|X}(y),dy+int _{a}^{infty }( ya)f_{Y|X}(y),dy\end{整列}}}
について微分する∂ ∂ a L = ∫ − ∞
aへ よ
| | X ( y) d y + ∫ a
∞− へ よ
| | X ( y) d y = 0
{ {frac {partial }{partial a}}L=int _{-infty}^{a}f_{Y|X}(y),dy+int _{a}^{ infty}-f_{Y|X}(y),dy=0}
これの意味は∫ − ∞
a へ ( y) d y = ∫ a
∞ へ ( y) d y
{ int _{-infty}^{a}f(y),dy=int_{a}^{infty}f(y),dy}
したがってふ よ
| | X ( a) = 0.5
{ F_{Y|X}(a)=0.5}
こちらもご覧ください
最小絶対偏差
平均絶対パーセント誤差
平均パーセント誤差
対称平均絶対パーセント誤差
参考文献
^ ウィルモット、コート J.; 松浦賢治 (2005 年 12 月 19 日). 「平均モデル性能の評価における二乗平均平方根誤差 (RMSE) に対する平均絶対誤差 (MAE) の利点」 . 気候研究。30:79~82.ドイ: 10.3354/cr030079 . ^ “2.5 予測精度の評価 | OTexts” . www.otexts.org 。2016 年5 月 18 日閲覧。
^ Hyndman, R. and Koehler A. (2005). 「予測精度の尺度の別の見方」 ^ ポンティアス・ジュニア、ロバート・ギルモア。トンテ、オルフンミラヨ。チェン、ハオ (2008)。「実変数を共有するマップ間の多重解像度比較のための情報の構成要素」。環境および生態学的統計。15 (2): 111–142. ドイ: 10.1007/s10651-007-0043-y . S2CID 21427573 . ^ ウィルモット、CJ。松浦和彦 . 「空間補間器の性能を評価するための誤差の次元測定の使用について」。地理情報科学の国際ジャーナル。20 : 89–102. ドイ: 10.1080/13658810500286976 . S2CID 15407960 . ^ ストロック、ダニエル (2011). 確率論。ケンブリッジ大学出版局。43ページ 。ISBN 978-0-521-13250-3. ^ ニコラス、アンドレ (2012-02-25). 「中央値は絶対偏差の合計を最小化します ($ {L}_{1} $ ノルム)」 . スタック交換。”