Measurement_in_quantum_mechanics
量子物理学では、測定とは数値結果を得るために物理システムをテストまたは操作することです。量子物理学による予測は、一般に確率論的です。どのような測定結果が発生するかを予測するための数学的ツールは、20 世紀に開発され、線形代数と関数解析を利用しています。
量子物理学は経験的に成功し、幅広い適用性があることが証明されています。しかし、より哲学的なレベルでは、測定概念の意味についての議論が続いています。
コンテンツ
1 数学的形式主義
1.1 自己随伴演算子としての「オブザーバブル」 1.2 射影測定 1.3 一般化された測定 (POVM) 1.4 測定による状態変化 1.5 例
2 測定概念の歴史
2.1 「古い量子論」 2.2 「新しい」量子論への移行 2.3 不確実性から隠されていない変数へ 2.4 計測装置としての量子系 2.5 デコヒーレンス
3 量子情報と計算
3.1 測定、エントロピー、識別可能性 3.2 量子回路 3.3 測定ベースの量子計算 3.4 量子トモグラフィー 3.5 量子計測学
4 実験室の実装
5 量子力学の解釈
6 こちらもご覧ください
7 ノート
8 参考文献
9 参考文献
数学的形式主義
自己随伴演算子としての「オブザーバブル」
正準量子化
量子力学では、各物理系はヒルベルト空間に関連付けられており、その各要素は物理系の可能な状態を表します。ジョン・フォン・ノイマンによって体系化されたアプローチは、「可観測」と呼ばれるヒルベルト空間上の自己随伴演算子による物理システムの測定を表します。 : 17 これらの観測量は、古典物理学でおなじみの測定可能な量の役割を果たします: 位置、運動量、エネルギー、角運動量など。ヒルベルト空間の次元は、連続自由度の量子物理学を定義するために使用される線上の平方可積分関数の空間の場合と同様に、無限になる場合があるいは、ヒルベルト空間は、スピンの自由度で発生するように、有限次元である場合が理論の多くの扱いは有限次元の場合に焦点を当てています。実際、量子力学に関する物理学の入門書では、連続値の可観測量と無限次元のヒルベルト空間で発生する数学的専門用語 (有界演算子と無界演算子の区別など) がよくわかりません。収束の問題 (ヒルベルト空間要素のシーケンスの極限もヒルベルト空間に属するかどうか)、カントール集合のような固有値の集合のエキゾチックな可能性。など。 : 79 これらの問題は、スペクトル理論を使用して十分に解決できます。 : 101 可能な限りそれらを避けます。
射影測定
参照:射影値メジャー
フォン ノイマン可観測量の固有ベクトルは、ヒルベルト空間の正規直交基底を形成し、その測定の可能な各結果は、基底を構成するベクトルの 1 つに対応します。密度演算子は、トレースが 1 に等しいヒルベルト空間上の半正定値演算子です。 定義できる各測定値について、その測定結果の確率分布を密度演算子から計算できます。 . そうするための手順は、次のように述べているボルン規則です。P (X I ) =
トレ( ΠI ρ
) { P(x_{i})=operatorname {tr} (Pi _{i}rho ),}
どこ ρ { rho}
は密度演算子、Π I
{ Pi _{i}}
は、測定結果に対応する基底ベクトルへの射影演算子です。X I { x_{i}}
. ボルン規則の確率で重み付けされたフォン ノイマン観測量の固有値の平均は、その観測量の期待値です。観測可能なもののために あ { A}
、与えられた量子状態の期待値 ρ { rho}
は ⟨ あ ⟩ =
トレ( あρ ) .
{ langle Arangle =operatorname {tr} (Arho ).}
ランク 1 射影である密度演算子は純粋な量子状態として知られており、純粋でないすべての量子状態は混合と指定されます。純粋な状態は、波動関数としても知られています。純粋な状態を量子システムに割り当てることは、そのシステムでの何らかの測定の結果についての確実性を意味します (つまり、P (X ) = 1
{ P(x)=1}
何らかの結果のためにX
{ x}
)。任意の混合状態は、一意の方法ではありませんが、純粋な状態の凸結合として記述できます。量子システムの状態空間は、それに割り当てることができる純粋な状態と混合された状態のすべてのセットです。
ボルン規則は、ヒルベルト空間内の各単位ベクトルに確率を関連付け、正規直交基底を構成する単位ベクトルの任意のセットについて、これらの確率の合計が 1 になるようにします。さらに、単位ベクトルに関連付けられた確率は、密度演算子と単位ベクトルの関数であり、そのベクトルを埋め込むための基底の選択などの追加情報の関数ではありません。グリーソンの定理は逆を確立します。これらの条件を満たす単位ベクトル (または、それらに射影する演算子) は、ボルン規則を密度演算子に適用する形式をとります。
一般化された測定 (POVM) POVM 関数解析と量子測定理論では、正の演算子値測度 (POVM) は、値がヒルベルト空間上の正の半定値演算子である測度です。POVM は射影値測定(PVM) の一般化であり、それに対応して、POVM によって記述される量子測定は、PVM によって記述される量子測定の一般化です。大雑把に言えば、POVM は PVM に対して、混合状態は純粋な状態に対してです。混合状態は、より大きなシステムのサブシステムの状態を指定するために必要です (シュレディンガー–HJW の定理を参照)。同様に、POVM は、より大きなシステムで実行される射影測定のサブシステムへの影響を記述するために必要です。POVM は、量子力学における最も一般的な種類の測定であり、場の量子論でも使用できます。それらは、量子情報の分野で広く使用されています。
有限次元のヒルベルト空間に作用する有限数の要素を持つ POVM の最も単純なケースでは、POVM は正の半正定 行列の集合です。{ ふ I } { {F_{i}}}
ヒルベルト空間で H { {mathcal {H}}}
その合計は単位行列 : 90 ∑ I = 1 n ふ I = I . { sum _{i=1}^{n}F_{i}=operatorname {I} .}
量子力学では、POVM 要素ふ I
{ F_{i}}
測定結果に関連付けられている I { i}
、量子状態の測定を行うときにそれを取得する確率 ρ { rho}
によって与えられます
問題 I ) =
トレ( ρふ I )
{ {text{Prob}}(i)=operatorname {tr} (rho F_{i})}
どこ
トレ
{ operatorname {tr} }
トレース演算子です。測定する量子状態が純粋な状態の場合
| |ψ ⟩
{ |psi rangle }
この式は
問題 I ) =
トレ( | |
ψ⟩ ⟨ ψ
| |ふ I ) = ⟨ ψ
| |ふ I
| |
ψ ⟩ { {text{Prob}}(i)=operatorname {tr} (|psi rangle langle psi |F_{i})=langle psi |F_{i}|psi rangle }
.
測定による状態変化
量子操作
量子系での測定は、一般に、その系の量子状態の変化をもたらします。POVM を書いても、この状態変化プロセスを説明するのに必要な完全な情報は得られません。 : 134 これを改善するために、各 POVM 要素を積に分解することにより、詳細情報が指定されます。え I = あ I † あ I .
{ E_{i}=A_{i}^{dagger}A_{i}.}
クラウスのオペレーターあ I
{ A_{i}}
Karl Krausにちなんで名付けられたは、状態変更プロセスの仕様を提供します。それらは必ずしも自己共役ではありませんが、積あ I † あ I
{ A_{i}^{dagger}A_{i}}
それは。測定を実行した結果え I
{ E_{i}}
が得られると、初期状態 ρ { rho}
に更新されますρ ρ 」=あ I ρ あ I † P r o b ( I) = あ I ρ あ I † レ( ρえ I ) .
{ rho to rho ‘={frac {A_{i}rho A_{i}^{dagger }}{mathrm {Prob} (i)}}={frac {A_{i }rho A_{i}^{dagger }}{operatorname {tr} (rho E_{i})}}.}
重要な特殊なケースは、Gerhart Lüdersにちなんで名付けられた Lüders 規則です。 POVM 自体が PVM である場合、Kraus 演算子はフォン ノイマン観測量の固有空間への射影であると見なすことができます。ρ ρ 」=Π I ρ Π I レ( ρΠ I ) .
{ rho to rho ‘={frac {Pi _{i}rho Pi _{i}}{operatorname {tr} (rho Pi _{i})}}.}
初期状態なら ρ { rho}
純粋で、プロジェクターΠ I
{ Pi _{i}}
ランク 1 を持ち、ベクトルへのプロジェクターとして書き込むことができます
| |ψ ⟩
{ |psi rangle }
と | |I ⟩
{ |irangle}
、 それぞれ。したがって、式は次のように単純化されます。ρ =
| |
ψ⟩ ⟨ ψ
| |ρ 」 = | |I ⟩ ⟨ I
| |ψ ⟩ ⟨ ψ
| |I ⟩ ⟨ I
| |
| |⟨ I
| |ψ ⟩
| |2 =
| |
I⟩ ⟨ I
| | . { rho =|psi rangle langle psi |to rho ‘={frac {|irangle langle i|psi rangle langle psi |irangle langle i| }{|langle i|psi rangle |^{2}}}=|irangle langle i|.}
これは、歴史的に「波束の縮小」または「波動関数の崩壊」として知られています。純粋な状態
| |I ⟩
{ |irangle}
フォン ノイマン観測量の確率 1 の予測を意味します。
| |I ⟩
{ |irangle}
固有ベクトルとして。量子論の入門書では、量子測定が立て続けに繰り返される場合、同じ結果が両方の回で発生すると言って、これを表現することがよく量子測定の物理的な実装には、光子の吸収のようなプロセスが含まれる可能性があるため、これは単純化しすぎです。測定後、再度測定する光子は存在しません。 : 91
正規化せずに POVM のすべての可能な測定後の状態を合計することにより、線形でトレースを維持する完全にポジティブなマップを定義できます。ρ ∑ I あ I ρ あ I † . { rho to sum _{i}A_{i}rho A_{i}^{dagger }.}
これは量子チャネルの例 : 150 であり、測定を行ったがその測定結果が失われた場合に量子状態がどのように変化するかを表していると解釈できます。 : 159
例

状態の明確な量子状態識別のための状態のブロッホ球表現 (青) と最適 POVM (赤)
| |ψ ⟩ =
| |0 ⟩
{ |psi rangle =|0rangle }
と | |φ ⟩ =( | |0 ⟩ +
| |1 ⟩ ) / 2
{ |varphi rangle =(|0rangle +|1rangle )/{sqrt {2}}}
. ブロッホ球では、直交状態は逆平行であることに注意して
有限次元ヒルベルト空間のプロトタイプの例は、ヒルベルト空間が 2 次元である量子システムであるqubitです。量子ビットの純粋な状態は、2 つの直交基底状態の線形結合として記述できます。
| |0 ⟩
{ |0rangle}
と | |1 ⟩
{ |1rangle }
複素係数:
| |
ψ⟩ = α
| |
0⟩ + β
| |
1 ⟩ { |psi rangle =alpha |0rangle +beta |1rangle }
での測定( | | 0 ⟩ | |1 ⟩ )
{ (|0rangle ,|1rangle )}
根拠は結果をもたらす
| |0 ⟩
{ |0rangle}
確率で
| | α | | 2 { |alpha |^{2}}
そして結果
| |1 ⟩
{ |1rangle }
確率で
| | β | | 2 { |beta |^{2}}
、したがって、正規化により、
| | α | |2 +
| | β | |2 = 1.
{ |alpha |^{2}+|beta |^{2}=1.}
量子ビットの任意の状態は、パウリ行列の線形結合として記述できます。2 × 2
{ 2times 2}
自己随伴行列: : 126 ρ =1 2( I+ X
σX y σ y ぜ σ ぜ
) { rho ={tfrac {1}{2}}left(I+r_{x}sigma _{x}+r_{y}sigma _{y}+r_{z}sigma _ {z}right),}
どこで実数( rX r y r ぜ)
{ (r_{x},r_{y},r_{z})}
は単位球内の点の座標であり、σX =( 01 1 0
) σy =( 0− I 私 0
) σぜ =( 10 0− 1 ) .
{ sigma _{x}={begin{pmatrix}0&1\1&0end{pmatrix}},quad sigma _{y}={begin{pmatrix}0&-i\i&0end {pmatrix}},quad sigma _{z}={begin{pmatrix}1&0\0&-1end{pmatrix}}.}
POVM 要素のトレースは 1 に等しく固定されていませんが、POVM 要素も同様に表すことができます。パウリ行列はトレースがなく、ヒルベルト-シュミット内積に関して互いに直交しているため、座標( rX r y r ぜ)
{ (r_{x},r_{y},r_{z})}
州の ρ { rho}
は、パウリ行列によって定義される 3 つのフォン ノイマン測定値の期待値です。 : 126 このような測定が量子ビットに適用される場合、Lüders の規則により、状態は測定結果に対応するそのパウリ行列の固有ベクトルに更新されます。の固有ベクトルσ ぜ
{ sigma _{z}}
は基底状態です
| |0 ⟩
{ |0rangle}
と | |1 ⟩
{ |1rangle }
、およびの測定σ ぜ
{ sigma _{z}}
は、「計算ベース」での測定と呼ばれることがよく : 76 計算ベースでの測定の後、 σX { sigma _{x}}
またσ y
{ sigma _{y}}
測定は最大限に不確実です。
キュービットのペアが一緒になって、ヒルベルト空間が 4 次元のシステムを形成します。このシステムでの 1 つの重要なフォン ノイマン測定は、ベル基底 によって定義されたものです: 36 4 つの最大エンタングル状態のセット:
| |Φ + ⟩ =1 2 ( | |0 ⟩ あ ⊗
| |0 ⟩ B +
| |1 ⟩ あ ⊗
| |1 ⟩ B )
| |Φ − ⟩ =1 2 ( | |0 ⟩ あ ⊗
| |0 ⟩ B −
| |1 ⟩ あ ⊗
| |1 ⟩ B )
| |Ψ + ⟩ =1 2 ( | |0 ⟩ あ ⊗
| |1 ⟩ B +
| |1 ⟩ あ ⊗
| |0 ⟩ B )
| |Ψ − ⟩ =1 2 ( | |0 ⟩ あ ⊗
| |1 ⟩ B −
| |1 ⟩ あ ⊗
| |0 ⟩ B )
{ {begin{aligned}|Phi ^{+}rangle &={frac {1}{sqrt {2}}}(|0rangle _{A}otimes |0rangle _ {B}+|1rangle _{A}otimes |1rangle _{B})\|Phi ^{-}rangle &={frac {1}{sqrt {2}}} (|0rangle _{A}otimes |0rangle _{B}-|1rangle _{A}otimes |1rangle _{B})\|Psi ^{+}rangle &={frac {1}{sqrt {2}}}(|0rangle _{A}otimes |1rangle _{B}+|1rangle _{A}otimes |0rangle _{B})\|Psi ^{-}rangle &={frac {1}{sqrt {2}}}(|0rangle _{A}otimes |1rangle _{B }-|1rangle _{A}otimes |0rangle _{B})end{整列}}}
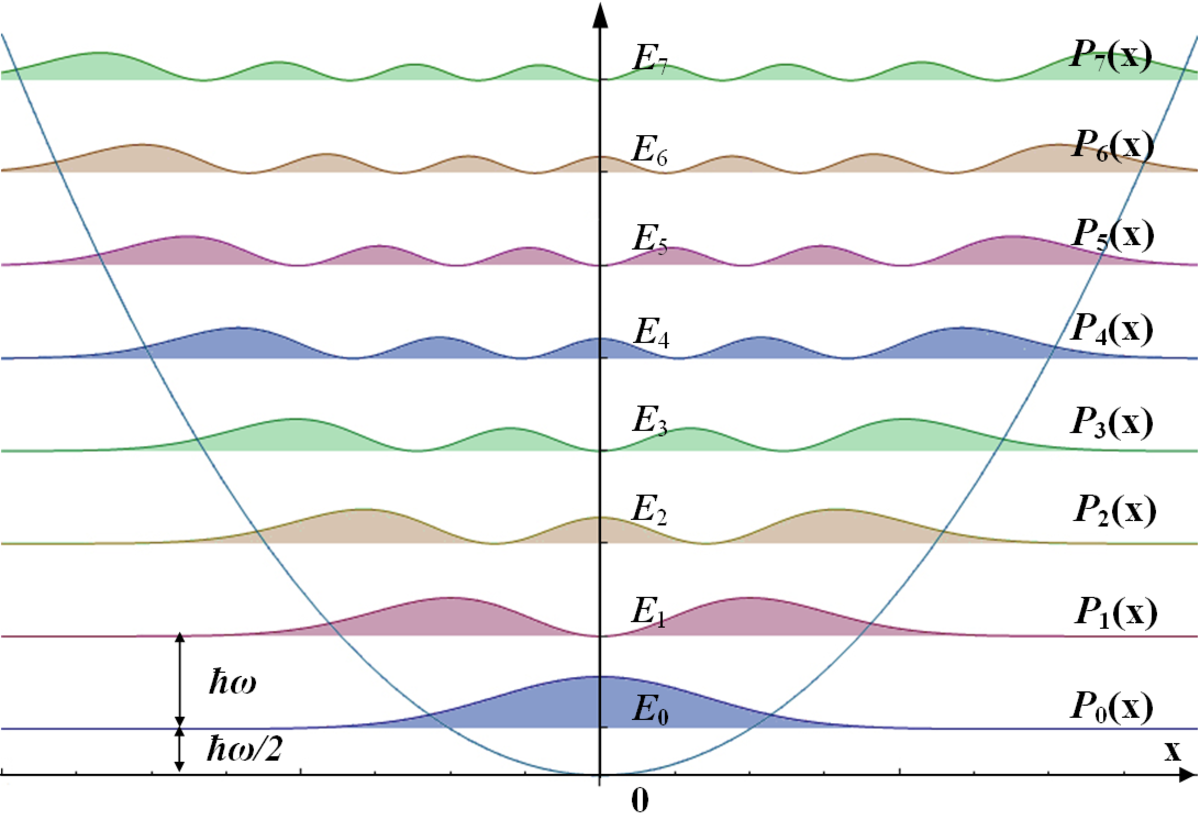
確率密度 P n(X )
{ P_{n}(x)}
エネルギー固有状態が与えられた位置測定の結果
| |n ⟩
{ |nrangle }
1D調和振動子の。
連続自由度に適用される量子力学の一般的で有用な例は、量子調和振動子です。 : 24 このシステムは、ハミルトニアンによって定義されます。 H = p2 2 メートル +1 2 メートルω 2X
2 { {H}={frac {{p}^{2}}{2m}}+{frac {1}{2}}momega ^{2}{x}^{2},}
どこ H { {H}}
、運動量演算子 p { {p}}
と位置演算子X
{ {x}}
は、実線上の 2 乗可積分関数のヒルベルト空間上の自己共役作用素です。エネルギー固有状態は、時間に依存しないシュレディンガー方程式を解きます。 H | |
n⟩ = え n | | n⟩ .
{ {H}|nrangle =E_{n}|nrangle .}
これらの固有値は、次の式で与えられることが示されます。え n = ℏ ω ( n +1 2
) { E_{n}=hbar omega left(n+{tfrac {1}{2}}right),}
これらの値は、発振器でのエネルギー測定の可能な数値結果を示します。調和振動子での位置測定の可能な結果のセットは連続的であるため、予測は確率密度関数の観点から記述されます。P (X )
{ P(x)}
からの無限小区間にある測定結果の確率を与えるX
{ x}
X+ dX
{ x+dx}
.
測定概念の歴史
「古い量子論」
古い量子論
古い量子論は、現代の量子力学よりも前の 1900 年から 1925 年の結果の集まりです。理論は決して完全ではなく、一貫性もありませんでしたが、むしろ古典力学に対するヒューリスティックな修正のセットでした。この理論は現在、現代の量子力学に対する半古典的な近似として理解されています。この時期の注目すべき結果には、プランクによる黒体放射スペクトルの計算、アインシュタインによる光電効果の説明、アインシュタインとデバイによる固体の比熱に関する研究、ボーアとファン レーウェンによる古典的な物理学は、反磁性、水素原子のボーアモデル、および相対論的効果を含むボーアモデルのアーノルド・ゾンマーフェルトの拡張を説明することはできません。

Stern-Gerlach の実験: 銀原子は不均一な磁場の中を移動し、スピンに応じて上下に偏向します。(1)炉、(2)銀原子ビーム、(3)不均一磁場、(4)古典的に期待される結果、(5)観測結果
1921 年に提案され、1922 年に実施されたスターン・ゲルラッハの実験 は、可能な結果の離散セットを持つ量子測定の典型的な例となった。元の実験では、銀原子は空間的に変化する磁場を通過して送られ、ガラス スライドなどの検出スクリーンに衝突する前に銀原子を偏向させました。磁気モーメントがゼロでない粒子は、磁場勾配により、直線経路から逸れます。画面には、粒子の量子化されたスピンにより、連続的な分布ではなく、離散的な蓄積点が表示されます。
「新しい」量子論への移行
英語で「運動学的および機械的関係の量子論的再解釈」として知られるハイゼンベルグによる 1925 年の論文は、量子物理学の成熟における極めて重要な瞬間を示しました。ハイゼンベルクは、「観測可能な」量のみに依存する原子現象の理論を開発しようとしました。当時、量子力学の後の標準的な提示とは対照的に、ハイゼンベルグは原子内に束縛された電子の位置を「観測可能」とは見なしていませんでした。代わりに、彼が関心を持っていた主な量は、原子によって放出または吸収された光の周波数でした。
不確実性原理はこの時代にさかのぼります。これは、電子の位置と運動量を同時に測定しようとする思考実験を分析する際にこの概念を導入したハイゼンベルグに起因することがよくしかし、ハイゼンベルグは、これらの測定値の「不確実性」が何を意味するかについて、正確な数学的定義を与え位置運動量の不確実性原理の正確な数学的記述はKennard、Pauli、およびWeylによるものであり、非交換観測量の任意のペアへの一般化はRobertsonおよびSchrödingerによるものです。
書き込みX
{ {x}}
と p
{ {p}}
それぞれ位置と運動量を表す自己共役演算子の場合、位置の標準偏差は次のように定義できます。σX =
⟨X2 − ⟨
2 { sigma _{x}={sqrt {langle {x}^{2}rangle -langle {x}rangle ^{2}}},}
運動量についても同様です。σ p = ⟨ p2 −
⟨ 2
{ sigma _{p}={sqrt {langle {p}^{2}rangle -langle {p}rangle ^{2}}}.}
Kennard–Pauli–Weyl の不確実性関係は次のとおりです。σX σ p ≥ ℏ 2 .
{ sigma _{x}sigma _{p}geq {frac {hbar }{2}}.}
この不等式は、量子粒子の準備が、位置の測定と運動量の測定の正確な予測を同時に意味することができないことを意味します。ロバートソンの不等式は、これを自己随伴演算子の任意のペアの場合に一般化します。 あ { A}
と B { B}
. これら 2 つの演算子の交換子は、= あ B − B
あ { =AB-BA,}
これにより、標準偏差の積の下限が得られます。σ あ σ B ≥
| |1 2I ⟨ ⟩
| | 1 2
| |⟨ ⟩
| | . { sigma _{A}sigma _{B}geq left|{frac {1}{2i}}langle rangle right|={frac {1}{ 2}}左|ラングルラングル右|.}
正準交換関係の代入= I ℏ
{ =ihbar }
、 1925 年にMax Bornによって最初に仮定された式は、不確定性原理の Kennard-Pauli-Weyl ステートメントを復元します。
不確実性から隠されていない変数へ
EPR のパラドックス、ベルの定理、ベル テスト
不確定性原理の存在は、当然、量子力学がより正確な理論への近似として理解できるかどうかという問題を提起します。量子論自体で扱われる量よりも基本的な「隠れた変数」が存在するのでしょうか? その知識によって、量子論が提供できるよりも正確な予測が可能になりますか? 一連の結果、最も重要なベルの定理は、そのような隠れ変数理論の広範なクラスが実際には量子物理学と両立しないことを示しています。
ベルは 1964 年に現在彼の名前で知られる定理を発表し、1935 年にアインシュタイン、ポドルスキー、ローゼンによって最初に提案された思考実験をより深く調査しました。 ベルの定理によれば、自然が実際に局所隠れ変数の理論に従って動作する場合、ベル テストの結果は特定の定量化可能な方法で制約されます。ベル検定が実験室で実行され、その結果が制約されていない場合、それらは局所的な隠れ変数が存在するという仮説と一致しません。このような結果は、量子力学の現象を、古典物理学の規則に沿った、より基本的な自然の記述という観点から説明する方法はないという立場を支持するでしょう。物理実験室では多くの種類のベル テストが実施されており、多くの場合、以前のベル テストの結果の有効性に原則として影響を与える可能性のある実験計画やセットアップの問題を改善することを目的としています。これは、「ベル テストの抜け穴を塞ぐ」こととして知られています。今日まで、ベル検定は、ローカルの隠れ変数の仮説が物理システムの振る舞いと一致しないことを発見しました。
計測装置としての量子系
Robertson–Schrödinger の不確実性原理は、2 つの観測量が交換されない場合、それらの間の予測可能性にトレードオフがあることを確立します。Wigner-Araki-Yanase の定理は、非可換性の別の結果を示しています。保存則の存在は、保存された量と交換できない観測量を測定できる精度を制限します。この行でのさらなる調査により、ウィグナー・ヤナセの歪曲情報が定式化されました。
歴史的に、量子物理学の実験はしばしば半古典的な用語で説明されてきました。たとえば、シュテルン・ゲルラッハ実験における原子のスピンは、量子自由度として扱われる可能性がありますが、原子はマクスウェル方程式の古典理論によって記述される磁場を通って移動すると見なされます。 : 24 しかし、実験装置を構築するために使用されるデバイスは、それ自体が物理システムであり、量子力学はそれらにも適用できるはずです。1950 年代から、Rosenfeldやvon Weizsäckerなどは、量子力学系を測定装置として扱うことができる場合に表現される整合性条件を開発しようとしました。測定装置の一部として使用されるシステムを半古典的にモデル化できる場合に関する基準の 1 つの提案は、Wigner関数に依存しています。非負。 : 375
デコヒーレンス
量子デコヒーレンス
不完全に分離されたシステムの量子状態は、通常、環境の量子状態と絡み合うように進化します。その結果、システムの初期状態が純粋であっても、システムと環境の結合状態の部分的なトレースを取得することによって検出された後の状態が混合されます。システムと環境の相互作用によって生成されるエンタングルメントのこの現象は、システムが原理的に明らかにすることができる量子力学のより風変わりな特徴をあいまいにする傾向がこの効果として知られている量子デコヒーレンスは、1970 年代に初めて詳細に研究されました。 (量子力学の極限として古典物理学がどのように得られるかについての以前の調査では、不完全に孤立したシステムの主題が調査されていましたが、エンタングルメントの役割は十分に理解されていませんでした。 )量子コンピューティングは、デコヒーレンスの有害な影響を回避することです。 : 239
説明するために、ρ S
{ rho _{S}}
システムの初期状態を示し、ρ え
{ rho _{E}}
環境の初期状態と H { H}
システムと環境の相互作用を指定するハミルトニアン。密度演算子ρ え
{ rho _{E}}
を対角化し、固有ベクトルへの射影の線形結合として書き込むことができます。ρ え = ∑ I p I
| |ψ I ⟩ ⟨ ψ I
| | . { rho _{E}=sum _{i}p_{i}|psi _{i}rangle langle psi _{i}|.}
持続時間の時間発展を表現する t { t}
ユニタリ演算子によってう = e − I H t / ℏ
{ U=e^{-iHt/hbar }}
、この進化後のシステムの状態はρ S 」=t r え う
[ ρ S ⊗( ∑I p I
| |ψ I ⟩ ⟨ ψ I
| |) ] う
† { rho _{S}’={rm {tr}}_{E}Uleft[rho _{S}otimes left(sum _{i}p_{i}|psi _{i}rangle langle psi _{i}|right)right]U^{dagger },}
に評価されるρ S 」=∑ I j p I
⟨ψ j
| | う | |ψ I ⟩ ρ S p I
⟨ψ I
| |う †
| |ψ j ⟩ .
{ rho _{S}’=sum _{ij}{sqrt {p_{i}}}langle psi _{j}|U|psi _{i}rangle rho _{ S}{sqrt {p_{i}}}langle psi _{i}|U^{dagger}|psi _{j}rangle .}
周囲の量ρ S
{ rho _{S}}
クラウス演算子として識別できるため、これは量子チャネルを定義します。
システムと環境の間の相互作用の形式を指定すると、一連の「ポインター状態」、つまり環境の変動に関して全体的なフェーズ要因を除いて (ほぼ) 安定しているシステムの状態を確立できます。ポインター状態のセットは、システムのヒルベルト空間の優先正規直交基底を定義します。 : 423
量子情報と計算
量子情報科学では、情報科学とその技術としての応用が量子力学的現象にどのように依存しているかを研究します。量子物理学における測定を理解することは、多くの点でこの分野にとって重要であり、その一部をここで簡単に概説します。
測定、エントロピー、識別可能性
フォン ノイマン エントロピーは、量子状態によって表される統計的不確実性の尺度です。密度行列の場合 ρ { rho}
、フォン ノイマン エントロピーは S ( ρ) = − t r( ρ
ログρ ) ;
{ S(rho )=-{rm {tr}}(rho log rho );}
書き込み ρ { rho}
固有ベクトルの基礎に関して、ρ = ∑ I λ I
| |
I⟩ ⟨ I
| | { rho =sum _{i}lambda _{i}|irangle langle i|,}
フォンノイマンエントロピーは S ( ρ) = − ∑ λ I
ログ
λI .
{ S(rho )=-sum lambda _{i}log lambda _{i}.}
これは、確率分布として解釈される固有値のセットのシャノン エントロピーです。したがって、フォン ノイマン エントロピーは、次の固有値で測定することによって定義される確率変数のシャノン エントロピーです。 ρ { rho}
. したがって、フォン ノイマン エントロピーは次の場合にゼロになります。 ρ { rho}
純粋です。 : 320 の von Neumann エントロピー ρ { rho}
量子状態が与えられた場合の最小シャノン エントロピーとして同等に特徴付けることができます。 ρ { rho}
、ランク 1 の要素を持つすべての POVM を最小化します。 : 323
量子情報理論で使用される他の多くの量も、測定の観点から動機と正当性を見出します。たとえば、量子状態間のトレース距離は、これら 2 つの量子状態が測定結果を暗示することができる確率の最大差に等しい: : 254 1 2 | | | | ρ− σ | |
| | = 最大0 ≤ え ≤ I
[ t r ( えρ ) − t r( えσ ) ] .
{ {frac {1}{2}}||rho -sigma ||=max _{0leq Eleq I}[{rm {tr}}(Erho )-{ rm {tr}}(Esigma )].}
同様に、2 つの量子状態の忠実度は、次のように定義されます。 ふ ( ρ σ) =(Tr ρ )
2 { F(rho ,sigma )=left(operatorname {Tr} {sqrt {{sqrt {rho }}sigma {sqrt {rho }}}}right)^{2 }、}
一方の状態が他方の準備の成功を識別するためのテストに合格する確率を表します。トレース距離は、Fuchs–van de Graaf の不等式: : 274 を介して忠実度の境界を提供します。1 − ふ( ρ σ ) ≤1 2 | | | | ρ− σ | |
| | 1− ふ( ρ σ) .
{ 1-{sqrt {F(rho ,sigma )}}leq {frac {1}{2}}||rho -sigma ||leq {sqrt {1-F( rho ,sigma )}}.}
量子回路

測定の回路表現。左側の 1 本の線は量子ビットを表し、右側の 2 本の線は従来のビットを表します。
量子回路
量子回路は量子計算のモデルであり、計算は一連の量子ゲートとそれに続く測定です。 : 93 ゲートは、 nビットレジスタの量子力学的アナログの可逆変換です。この類似の構造は、n – qubitレジスタと呼ばれます。様式化されたポインター ダイヤルとして回路図に描かれた測定値は、計算のステップが実行された後、どこでどのように量子コンピューターから結果が取得されるかを示します。一般性を失うことなく、標準回路モデルを使用できます。このモデルでは、一連のゲートが単一キュービットのユニタリ変換であり、キュービットのペアに対する制御された NOT ゲートであり、すべての測定値が計算ベースに : 93
測定ベースの量子計算
一方向量子コンピューター
測定ベースの量子計算 (MBQC) は、質問に対する答えが、非公式に言えば、コンピューターとして機能する物理システムを測定する行為で作成される量子コンピューティングのモデルです。 : 317
量子トモグラフィー
量子トモグラフィー
量子状態トモグラフィーは、量子測定の結果を表す一連のデータが与えられると、それらの測定結果と一致する量子状態が計算されるプロセスです。 CT スキャンのように、トモグラフィーを通して撮影されたスライスから 3 次元画像を再構成するトモグラフィーとの類似性から名付けられました。量子状態のトモグラフィーは、量子チャネルのトモグラフィーや測定のトモグラフィーに拡張することができます。
量子計測学
量子計測学
量子計測は、量子効果を利用して長さを測定できる精度を高めるなど、一般に古典物理学で意味を持っていた量の測定を支援するために量子物理学を使用することです。有名な例は、重力波に対する感度を高めたLIGO実験への圧搾光の導入です。
実験室の実装
量子測定の数学が適用できる物理的手順の範囲は非常に広いです。被験者の初期の実験室手順には、スペクトル線の記録、写真フィルムの暗化、シンチレーションの観察、雲室での痕跡の発見、ガイガーカウンターからのクリック音の聴取が含まれていました。「検出器のクリック」として抽象化された測定結果の説明など、この時代の言葉が残っています。
二重スリット実験は、通常、電子または光子を使用して説明される、量子干渉の典型的な例です。光子の挙動の波のような側面と粒子のような側面の両方が重要な領域で実行される最初の干渉実験は、1909 年のGI テイラーのテストでした。テイラーはスモーク ガラスのスクリーンを使用して、彼の装置を通過する光を減衰させました。現代の言葉で言えば、一度に干渉計のスリットを照らす光子は 1 つだけです。彼は干渉パターンを写真乾板に記録しました。最も暗い光の場合、必要な露出時間は約 3 か月でした。 1974 年、イタリアの物理学者 Pier Giorgio Merli、Gian Franco Missiroli、およびGiulio Pozziは、単一電子とテレビ管を使用して二重スリット実験を実施しました。四半世紀後、ウィーン大学のチームは、干渉計を通過したバッキーボールがレーザーによってイオン化され、イオンが電子の放出を誘発するバッキーボールの干渉実験を行いました。順番に増幅され、電子増倍管によって検出されました。
現代の量子光学実験では、単一光子検出器を使用できます。たとえば、2018 年の「BIG Bell テスト」では、実験室のセットアップのいくつかで単一光子アバランシェ ダイオードが使用されました。別の実験室のセットアップでは、超伝導量子ビットが使用されました。超伝導キュービットの測定を実行する標準的な方法は、共振器の特性周波数がキュービットの状態に応じてシフトするようにキュービットを共振器と結合し、共振器がどのように反応するかを観察することによってこのシフトを検出することです。プローブ信号に。
量子力学の解釈
量子力学の解釈

ニールス・ボーアとアルバート・アインシュタインは、ライデンのポール・エーレンフェストの家でここに描かれています(1925 年 12月) 。
量子物理学は実際には成功した理論であるという科学者の間のコンセンサスにもかかわらず、より哲学的なレベルでは意見の相違が続いています。量子基礎として知られる分野での多くの議論は、量子力学における測定の役割に関係しています。ボルンの規則から計算された確率に最も適している確率論の解釈が含まれます。そして、量子測定結果の明らかなランダム性が基本的なものなのか、それともより深い決定論的プロセスの結果なのか。 このような疑問に対する答えを提示する世界観は、量子力学の「解釈」として知られています。物理学者N. デビッド マーミンがかつて皮肉を言ったように、「新しい解釈は毎年現れます。決して消えることはありません。」
量子基盤内の中心的な関心事は「量子測定問題」ですが、この問題がどのように区切られているか、また、それを 1 つの問題として数えるべきか、それとも複数の問題として数えるべきかは論争の的となっています。 主な関心事は、明らかに異なるタイプの時間進化の間の不一致のように見えることです。フォン・ノイマンは、量子力学には「2 つの根本的に異なるタイプ」の量子状態変化が含まれていると宣言しました。 : §V.1 第一に、測定プロセスを伴う変化があり、第二に、測定がない場合のユニタリ時間発展が前者は確率論的で不連続であり、後者は決定論的で連続的であるとフォン・ノイマンは書いています。この二分法は、その後の議論の基調となっています。 量子力学のいくつかの解釈は、2 つの異なるタイプの時間発展への依存を不快なものと見なし、量子論が歴史的に提示された方法の欠陥として、どちらか一方を呼び出すタイミングのあいまいさを考慮しています。これらの解釈を強化するために、彼らの支持者は、「測定」を二次的な概念と見なし、測定プロセスの一見確率論的な効果をより基本的な決定論的ダイナミクスへの近似として推測する方法を導き出すことに取り組んできました。しかし、このプログラムを実装する正しい方法、特にボルン規則を使用して確率を計算することを正当化する方法については、支持者の間でコンセンサスが得られ 他の解釈では、量子状態を量子系に関する統計情報とみなし、量子状態の急激で不連続な変化は問題ではなく、単に利用可能な情報の更新を反映していると主張している. この考え方について、ベルは「誰の情報?何についての情報? 」と尋ねた。これらの質問に対する答えは、情報指向の解釈の支持者によって異なります。
こちらもご覧ください
アインシュタインの思考実験
ホレボの定理
量子誤り訂正
量子限界
量子論
量子ゼノ効果
シュレディンガーの猫
SIC-POVM
ノート
^ Hellwig と Kraus は、もともと 2 つのインデックスを持つ演算子を導入しました。あ I j
{ A_{ij}}
、 そのような∑ j あ I j あ I j †= え I
{ textstyle sum _{j}A_{ij}A_{ij}^{dagger}=E_{i}}
. 追加のインデックスは、測定結果の確率の計算には影響しませんが、測定後の状態が次の値に比例する状態で、状態更新ルールで役割を果たします。∑ j あ I j † ρ あ I j { textstyle sum _{j}A_{ij}^{dagger}rho A_{ij}}
. これは代表的なものと見なすことができますえ I
{ textstyle E_{i}}
よりきめの細かい POVM の複数の結果をまとめた粗視化として。 2 つのインデックスを持つ Kraus 演算子は、システムと環境の相互作用の一般化されたモデルでも発生します。 : 364
^ Stern-Gerlach 実験で使用されたガラス板は、て安価な葉巻の硫黄にさらされるまで、適切に暗くならなかった
参考文献
^ ホレボ、アレクサンダー S. (2001). 量子論の統計的構造。物理学の講義ノート。スプリンガー。ISBN 3-540-42082-7. OCLC 318268606。
^
ペレス、アッシャー(1995)。量子論: 概念と方法。クルワー アカデミック パブリッシャーズ。ISBN 0-7923-2549-4.
^ タオ、テリー(2014 年 8 月 12 日)。「アビラ、バルガヴァ、ヘアラー、ミルザハニ」 . 新機能. 2020年2月9日閲覧。
^ カークパトリック、カザフスタン 。「シュレディンガー-HJW定理」。物理文字の基礎。19 (1): 95–102. arXiv : quant-ph/0305068 . Bibcode : 2006FoPhL..19…95K . ドイ: 10.1007/s10702-006-1852-1 . ISSN 0894-9875。S2CID 15995449 .
^ グリーソン、アンドリュー M. (1957)。「ヒルベルト空間の閉部分空間の測定」 . インディアナ大学数学ジャーナル。6 (4): 885–893。ドイ: 10.1512/iumj.1957.6.56050 . MR 0096113 .
^ ブッシュ、ポール(2003)。「量子状態と一般化された観測量: グリーソンの定理の簡単な証明」. フィジカル レビュー レター。91 (12): 120403. arXiv : quant-ph/9909073 . ビブコード: 2003PhRvL..91l0403B . ドイ: 10.1103/PhysRevLett.91.120403 . PMID 14525351。S2CID 2168715 .
^ 洞窟、カールトン M .; フックス、クリストファーA。Manne、Kiran K.; レネス、ジョセフ M. (2004)。「一般化された測定のための量子確率規則のグリーソン型導出」。物理学の基礎。34 (2): 193–209. arXiv : quant-ph/0306179 . ビブコード: 2004FoPh…34..193C . ドイ: 10.1023/B:FOOP.0000019581.00318.a5 . S2CID 18132256 .
^ Peres, アッシャー; Terno、Daniel R. (2004)。「量子情報と相対性理論」。現代物理学のレビュー。76 (1): 93–123. arXiv : quant-ph/0212023 . ビブコード: 2004RvMP…76…93P . 土井: 10.1103/RevModPhys.76.93 . S2CID 7481797 . ^
ニールセン、マイケル・A .; Chuang、Isaac L. (2000)。量子計算と量子情報(第 1 版)。ケンブリッジ:ケンブリッジ大学出版局。ISBN 978-0-521-63503-5. OCLC 634735192。
^ g h i j
ワイルド、マーク M. (2017)。量子情報理論(第 2 版)。ケンブリッジ大学出版局。arXiv : 1106.1445 . ドイ: 10.1017/9781316809976.001 . ISBN 9781107176164. OCLC 973404322。S2CID 2515538 .
^ Hellwig、K.-E。Kraus, K. (1969 年 9月)。「純粋な操作と測定」 . 数理物理学におけるコミュニケーション。11 (3): 214–220. ドイ: 10.1007/BF01645807 . ISSN 0010-3616 . S2CID 123659396 .
^ クラウス、カール(1983)。状態、効果、操作: 量子論の基本概念。テキサス大学オースティン校で数理物理学の講義を行っています。巻。190. スプリンガー出版。ISBN 978-3-5401-2732-1. OCLC 925001331 .
^ バーナム、ハワード。ニールセン, マサチューセッツ州; シューマッハ、ベンジャミン(1998 年 6 月 1 日)。「ノイズの多い量子チャネルを介した情報伝送」。フィジカルレビューA. 57 (6): 4153–4175. arXiv : quant-ph/9702049 . ビブコード: 1998PhRvA..57.4153B . ドイ: 10.1103/PhysRevA.57.4153 . ISSN 1050-2947 . S2CID 13717391 .
^ フックス、クリストファーA。ジェイコブス、カート (2001 年 5 月 16 日)。「有限強度量子測定の情報トレードオフ関係」。フィジカルレビューA. 63 (6): 062305. arXiv : quant-ph/0009101 . ビブコード: 2001PhRvA..63f2305F . ドイ: 10.1103/PhysRevA.63.062305 . ISSN 1050-2947 . S2CID 119476175 .
^ Poulin、David (2005 年 2 月 7 日)。「巨視的観測物」。フィジカルレビューA. 71 (2): 022102. arXiv : quant-ph/0403212 . ビブコード: 2005PhRvA..71b2102P . ドイ: 10.1103/PhysRevA.71.022102 . ISSN 1050-2947 . S2CID 119364450 .
^ Lüders、Gerhart (1950)。””Uber die Zustandsänderung durch den Messprozeß””. Annalen der Physik . 443 (5–8): 322. Bibcode : 1950AnP…443..322L . doi : 10.1002/andp.19504430510 .KA カークパトリックによる翻訳
Lüders、Gerhart (2006 年 4 月 3 日)。「採寸工程による状態変化について」Annalen der Physik . 15 (9): 663–670. arXiv : quant-ph/0403007 . ビブコード: 2006AnP…518..663L . doi : 10.1002/andp.200610207 . S2CID 119103479 .
^ ブッシュ、ポール。Lahti、Pekka (2009)、Greenberger、Daniel。ヘンチェル、クラウス。Weinert, Friedel (eds.), “”Lüders Rule””, Compendium of Quantum Physics , Springer Berlin Heidelberg, pp. 356–358, doi : 10.1007/978-3-540-70626-7_110 , ISBN 978-3-540-70622-9
^ Peres, アッシャー; Terno、Daniel R. (1998)。「非直交量子状態間の最適な区別」。Journal of Physics A: 数学および一般。31 (34): 7105–7111. arXiv : quant-ph/9804031 . ビブコード: 1998JPhA…31.7105P . ドイ:10.1088/0305-4470/31/34/013。ISSN 0305-4470。S2CID 18961213 . ^
リーフェル、エレノア G .; Polak、Wolfgang H. (2011 年 3 月 4 日)。量子コンピューティング: 穏やかな紹介. MITプレス。ISBN 978-0-262-01506-6.
^ ワインバーグ、スティーブン(2015)。量子力学の講義(第二版)。ケンブリッジ、イギリス: ケンブリッジ大学出版局。ISBN 978-1-107-11166-0. OCLC 910664598。
^ パイス、エイブラハム(2005)。微妙なところが主です: アルバート・アインシュタインの科学と生涯(図版)。オックスフォード大学出版局。p。28.ISBN _ 978-0-19-280672-7.
^ ter Haar、D.(1967)。古い量子論。ペルガモンプレス。206頁 。ISBN 978-0-08-012101-7.
^ 「半古典近似」 . 数学の百科事典。2020年2月1日閲覧。
^ 桜井 JJ ; Napolitano、J.(2014)。「量子ダイナミクス」。現代の量子力学。ピアソン。ISBN 978-1-292-02410-3. OCLC 929609283。
^ ゲルラッハ、W.; スターン、O.(1922)。””Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld””. Zeitschrift für Physik . 9 (1): 349–352。ビブコード: 1922ZPhy….9..349G . ドイ: 10.1007/BF01326983 . S2CID 186228677 .
^ ゲルラッハ、W.; スターン、O.(1922)。「Das magnetische Moment des Silberatoms」。Zeitschrift für Physik . 9 (1): 353–355。ビブコード: 1922ZPhy….9..353G . ドイ: 10.1007/BF01326984 . S2CID 126109346 .
^ ゲルラッハ、W.; スターン、O.(1922)。””Der experimentelle Nachweis des magnetischen Moments des Silberatoms”” . Zeitschrift für Physik . 8 (1): 110–111。ビブコード: 1922ZPhy….8..110G . ドイ:10.1007/BF01329580。S2CID 122648402 .
^ アラン・フランクリンとスロボダン・ペロビッチ。「物理学の実験、付録 5」 . Edward N. Zalta (編)。スタンフォード哲学百科事典(2016 年冬版) . 2018年8 月 14 日閲覧。
^ フリードリヒ、B。Herschbach、D.(2003)。「スターンとゲルラッハ: 悪い葉巻が原子物理学の方向転換にどのように役立ったか」 . 今日の物理学。56 (12): 53. Bibcode : 2003PhT….56l..53F . ドイ: 10.1063/1.1650229 . S2CID 17572089 .
^ 朱、広天。シン、チャンドラレカ。「シュテルン・ゲルラッハ実験による学生の量子力学の理解の向上」 . 物理学のアメリカのジャーナル。79 (5): 499–507. arXiv : 1602.06367 . ビブコード: 2011AmJPh..79..499Z . ドイ: 10.1119/1.3546093 . ISSN 0002-9505 . S2CID 55077698 .
^ van der Waerden, BL (1968)。「はじめに、パート II」。量子力学の源。ドーバー。ISBN 0-486-61881-1.
^ ブッシュ、ポール。ラハティ、ペッカ。ヴェルナー、ラインハルト F. (2013 年 10 月 17 日)。「ハイゼンベルグのエラー-妨害関係の証明」。フィジカル レビュー レター。111 (16): 160405. arXiv : 1306.1565 . ビブコード: 2013PhRvL.111p0405B . ドイ: 10.1103/PhysRevLett.111.160405 . ISSN 0031-9007 . PMID 24182239。S2CID 24507489 .
^ Appleby、David Marcus (2016 年 5 月 6 日)。「量子エラーと擾乱: ブッシュ、ラハティ、ヴェルナーへの対応」 . エントロピー。18 (5) : 174。arXiv : 1602.09002。ビブコード: 2016Entrp..18..174A . ドイ: 10.3390/e18050174 .
^ ランダウ, LD ; リフシッツ、EM (1977)。量子力学: 非相対論。巻。3 (第 3 版)。ペルガモンプレス。ISBN 978-0-08-020940-1. OCLC 2284121 .
^ 生まれた、M .; ヨルダン、P. (1925)。「Zur Quantenmechanik」。Zeitschrift für Physik . 34 (1): 858–888. ビブコード: 1925ZPhy…34..858B . ドイ: 10.1007/BF01328531 . S2CID 186114542 .
^ ベル、JS(1964)。「アインシュタイン ポドルスキー ローゼン パラドックスについて」 (PDF) . Physics Physique Физика . 1 (3): 195–200。doi : 10.1103/PhysicsPhysiqueFizika.1.195 .
^ アインシュタイン、A ; ポドルスキー、B ; ローゼン、N (1935 年 5 月 15 日)。「物理的現実の量子力学的記述は完全であると見なすことができますか?」. フィジカルレビュー。47 (10): 777–780. Bibcode : 1935PhRv…47..777E . ドイ: 10.1103/PhysRev.47.777 .
^ BIG ベル テスト コラボレーション (2018 年 5 月 9 日)。「人間の選択によるローカルリアリズムへの挑戦」. 自然。557 (7704): 212–216. arXiv : 1805.04431 . ビブコード: 2018Natur.557..212B . ドイ: 10.1038/s41586-018-0085-3 . PMID 29743691。S2CID 13665914 .
^ ウォルコーバー、ナタリー(2017 年 2 月 7 日)。「実験は量子の奇妙さを再確認する」 . クォンタマガジン。2020年2月8日閲覧。
^ たとえば、次を参照して
Wigner, EP (1995), “”Die Messung quantenmechanischer Operatoren””, Mehra, Jagdish (ed.), Philosophical Reflections and Syntheses , Springer Berlin Heidelberg, pp. 147–154, doi : 10.1007/978-3-642-78374- 6_10、ISBN 978-3-540-63372-3
荒木藤宏 柳瀬睦夫 (1960 年 10 月 15 日)。「量子力学演算子の測定」。フィジカルレビュー。120 (2): 622–626. ビブコード: 1960PhRv..120..622A . ドイ: 10.1103/PhysRev.120.622 . ISSN 0031-899X .
柳瀬睦夫 (1961 年 7 月 15 日)。「最適測定器」。フィジカルレビュー。123 (2): 666–668. ビブコード: 1961PhRv..123..666Y . ドイ: 10.1103/PhysRev.123.666 . ISSN 0031-899X .
アフマディ、メディ; ジェニングス、デビッド。ルドルフ、テリー (2013 年 1 月 28 日)。「ウィグナー・荒木・柳瀬の定理と非対称性の量子資源理論」 . 物理学の新しいジャーナル。15 (1): 013057. arXiv : 1209.0921 . ビブコード: 2013NJPh…15a3057A . ドイ: 10.1088/1367-2630/15/1/013057 . ISSN 1367-2630。
^ 羅神龍(2003)。「Wigner-Yanase Skew Information and Uncertainty Relations」. フィジカル レビュー レター。91 (18): 180403. Bibcode : 2003PhRvL..91r0403L . ドイ: 10.1103/PhysRevLett.91.180403 . PMID 14611271。
^ カミレリ、K.Schlosshauer、M.(2015)。「実験の哲学者としてのニールス・ボーア:デコヒーレンス理論はボーアの古典的概念の教義に挑戦しますか?」. 現代物理学の歴史と哲学の研究。49 : 73–83. arXiv : 1502.06547 . ビブコード: 2015SHPMP..49…73C . ドイ: 10.1016/j.shpsb.2015.01.005 . S2CID 27697360 .
^ Schlosshauer、M.(2019)。「量子デコヒーレンス」。物理レポート。831 : 1–57。arXiv : 1911.06282 . Bibcode : 2019PhR…831….1S . ドイ: 10.1016/j.physrep.2019.10.001 . S2CID 208006050 .
^ デイビッド・ディビンセンゾ; Terhal、バーバラ(1998 年 3月)。「デコヒーレンス: 量子計算の障害」. 物理学の世界。11 (3): 53–58. ドイ:10.1088/2058-7058/11/3/32。ISSN 0953-8585 .
^ Terhal、バーバラ M. (2015 年 4 月 7 日)。「量子メモリの量子誤り訂正」。現代物理学のレビュー。87 (2): 307–346. arXiv : 1302.3428 . ビブコード: 2013arXiv1302.3428T . 土井: 10.1103/RevModPhys.87.307 . ISSN 0034-6861 . S2CID 118646257 .
^ R.ラウセンドルフ; DE ブラウン & HJ ブリーゲル (2003)。「クラスター状態に関する測定ベースの量子計算」。フィジカルレビューA. 68 (2): 022312. arXiv : quant-ph/0301052 . ビブコード: 2003PhRvA..68b2312R . ドイ: 10.1103/PhysRevA.68.022312 . S2CID 6197709 .
^ チャイルズ、アンドリュー・M .; Leung、Debbie W .; Nielsen、Michael A. (2005 年 3 月 17 日)。「量子計算のための測定ベースのスキームの統一された導出」。フィジカルレビューA. 71 (3): 032318。arXiv : quant -ph/0404132。ビブコード: 2005PhRvA..71c2318C . ドイ: 10.1103/PhysRevA.71.032318 . ISSN 1050-2947 . S2CID 27097365 .
^ グラナード、クリストファー。クームズ、ジョシュア。Cory、DG (2016 年 1 月 1 日)。「実用的なベイジアン トモグラフィー」。物理学の新しいジャーナル。18 (3): 033024. arXiv : 1509.03770 . ビブコード: 2016NJPh…18c3024G . ドイ: 10.1088/1367-2630/18/3/033024。ISSN 1367-2630。S2CID 88521187 .
^ ランディーン、JS。Feito、A。Coldenstrodt-Ronge、H.; プレグネル、KL; シルバーホーン、Ch; ラルフ、TC。Eisert、J。プレニオ、MB。アイオワ州ウォームズリー (2009)。「量子検出器のトモグラフィー」。自然物理学。5 (1): 27–30. arXiv : 0807.2444 . Bibcode : 2009NatPh…5…27L . ドイ: 10.1038/nphys1133 . ISSN 1745-2481。S2CID 119247440 .
^ ブラウンスタイン、サミュエル L.; 洞窟、カールトン M. (1994 年 5 月 30 日)。「統計距離と量子状態の幾何学」. フィジカル レビュー レター。72 (22): 3439–3443。ビブコード: 1994PhRvL..72.3439B . ドイ: 10.1103/physrevlett.72.3439 . PMID 10056200。
^ コバーライン、ブライアン (2019 年 12 月 5 日)。「LIGOは光を絞って、空の空間の量子ノイズを克服します」 . 今日の宇宙。2020年2月2日閲覧。
^ ボール、フィリップ(2019 年 12 月 5 日)。「焦点: 重力波検出器からより多くを絞り出す」. 物理学。12 . doi : 10.1103/Physics.12.139 . S2CID 216538409 .
^ Peierls、Rudolf (1991)。「「測定」を擁護して””. Physics World . 4 (1): 19–21. doi : 10.1088/2058-7058/4/1/19 . ISSN 2058-7058 .
^ バラド、カレン(2007)。途中で宇宙に出会う:量子物理学と物質と意味の絡み合い。デューク大学出版局。ISBN 978-0-8223-3917-5. OCLC 1055296186。
^ Englert、Berthold-Georg (2013 年 11 月 22 日)。「量子論について」。欧州物理ジャーナルD. 67 (11) : 238。arXiv : 1308.5290。ビブコード: 2013EPJD…67..238E . ドイ: 10.1140/epjd/e2013-40486-5 . ISSN 1434-6079。S2CID 119293245 .
^ テイラー、GI(1909)。「微弱な光による干渉縞」。ケンブリッジ哲学協会の議事録。15 :114~115。
^ Gbur、グレッグ(2018 年 8 月 25 日)。「テイラーは(微弱な)光を見る(1909)」 . 星の頭蓋骨。2020年10月24日閲覧。
^ Merli、PG。ミシロリ、GF; Pozzi、G(1976)。「電子干渉現象の統計的側面について」. 物理学のアメリカのジャーナル。44 (3): 306–307. ビブコード: 1976AmJPh..44..306M . ドイ: 10.1119/1.10184 .
^ Arndt、Markus。オラフ・ネアーズ。Vos-Andreae、ジュリアン。ケラー、クラウディア。Van Der Zouw、Gerbrand。Zeilinger、アントン(1999)。「C60分子の波と粒子の二重性」. 自然。401 (6754): 680–682. ビブコード: 1999Natur.401..680A . ドイ:10.1038/44348。PMID 18494170。S2CID 4424892 .
^ クランツ、フィリップ。ベングソン、アンドレアス。シモエン、ミカエル。グスタフソン、シモン。Shumeiko、Vitaly。オリバー、WD; ウィルソン、CM。デルシング、パー。バイランダー、ジョナス (2016 年 5 月 9 日)。「ジョセフソンパラメトリック発振器を使用した超伝導キュービットのシングルショット読み出し」 . ネイチャーコミュニケーションズ。7 (1): 11417。arXiv : 1508.02886。Bibcode : 2016NatCo…711417K . ドイ: 10.1038/ncomms11417 . ISSN 2041-1723 . PMC 4865746 . PMID 27156732。
^ シュロスハウアー、マクシミリアン。コフラー、ヨハネス。Zeilinger、アントン(2013 年 1 月 6 日)。「量子力学に対する基本的な態度のスナップショット」. 科学の歴史と哲学の研究パートB:現代物理学の歴史と哲学の研究。44 (3): 222–230. arXiv : 1301.1069 . ビブコード: 2013SHPMP..44..222S . ドイ: 10.1016/j.shpsb.2013.04.004 . S2CID 55537196 .
^ カベッロ、アダン (2017)。「量子論の解釈:狂気の地図」. ロンバルディ、オリンピアで; フォーティン、セバスチャン。ホリック、フェデリコ。ロペス、クリスティアン(編)。量子情報とは . ケンブリッジ大学出版局。pp.138–143。arXiv : 1509.04711 . ビブコード: 2015arXiv150904711C . ドイ: 10.1017/9781316494233.009 . ISBN 9781107142114. S2CID 118419619 .
^ シェーファー、キャスリン。Barreto Lemos、ガブリエラ (2019 年 5 月 24 日)。「消し去るもの:量子物理学の「何」と「だから何」の紹介」. 科学の基礎。26 : 7–26. arXiv : 1908.07936 . ドイ: 10.1007/s10699-019-09608-5 . ISSN 1233-1821。S2CID 182656563 .
^ Mermin, N. David (2012 年 7 月 1 日)。「解説:量子力学:シフティスプリットの修正」 . 今日の物理学。65 (7): 8–10. ビブコード: 2012PhT….65g…8M . ドイ: 10.1063/PT.3.1618 . ISSN 0031-9228 .
^ バブ、ジェフリー; Pitowsky、Itamar (2010)。「量子力学に関する 2 つのドグマ」。多くの世界?. オックスフォード大学出版局。pp.433–459。arXiv : 0712.4258 . ISBN 9780199560561. OCLC 696602007。
^ ジョン・フォン・ノイマン(2018)。ウィーラー、ニコラス A. (ed.)。量子力学の数学的基礎。新版。ロバート・T・ベイヤー訳。プリンストン大学出版局。ISBN 9-781-40088-992-1. OCLC 1021172445。
^ Wigner, EP (1995), “”Review of the Quantum-Mechanical Measurement Problem””, in Mehra, Jagdish (ed.), Philosophical Reflections and Syntheses , Springer Berlin Heidelberg, pp. 225–244, doi : 10.1007/978-3- 642-78374-6_19、ISBN 978-3-540-63372-3
^ フェイ、ヤン(2019)。「量子力学のコペンハーゲン解釈」 . Zalta では、Edward N. (ed.)。哲学のスタンフォード百科事典。スタンフォード大学の形而上学研究所。
^ ベル、ジョン(1990)。「「測定」に反対する””. Physics World . 3 (8): 33–41. doi : 10.1088/2058-7058/3/8/26 . ISSN 2058-7058 .
^ ケント、エイドリアン(2010)。「1つの世界対多:進化、確率、および科学的確認に関するエベレッティの説明の不十分さ」. 多くの世界?. オックスフォード大学出版局。pp.307–354。arXiv : 0905.0624 . ISBN 9780199560561. OCLC 696602007。
^ バレット、ジェフリー(2018)。「エベレットの量子力学の相対状態定式化」 . Zalta では、Edward N. (ed.)。哲学のスタンフォード百科事典。スタンフォード大学の形而上学研究所。
^ ヒーリー、リチャード (2016)。「量子理論の量子ベイジアンとプラグマティストの見解」 . Zalta では、Edward N. (ed.)。哲学のスタンフォード百科事典。スタンフォード大学の形而上学研究所。
参考文献![]()
ウィキクォートに量子力学における測定
に関する引用が
ホイーラー、ジョン A .; Zurek、Wojciech H.、編。(1983)。量子論と測定。プリンストン大学出版局。ISBN 978-0-691-08316-2.
ウラジミール・B・ブラギンスキーとファリド・ヤ。カリリ (1992)。量子測定。ケンブリッジ大学出版局。ISBN 978-0-521-41928-4.
ジョージ S. グリーンスタイン & アーサー G. ザジョン (2006)。量子チャレンジ: 量子力学の基礎に関する現代研究(第 2 版)。ISBN 978-0763724702.
Orly Alterと山本義久(2001)。単一システムの量子測定。ニューヨーク州ニューヨーク:ワイリー。ドイ: 10.1002/9783527617128 . ISBN 9780471283089.”
