Planar_algebra
数学では、平面代数はII 1サブ因子の標準不変量に関するVaughan Jonesの研究で初めて登場しました。これらは、多くのノット不変量(特にジョーンズ多項式)に適切な代数枠組みも提供し、もつれ組成に関するコバノフ ホモロジーの特性を記述する際に使用されています。 任意の部分因子平面代数は、トンプソン群のユニタリー表現の族を提供します。任意の有限群 (および量子一般化) は平面代数としてエンコードできます。
コンテンツ
1 意味
1.1 平面的なもつれ 1.2 構成 1.3 平面オペラド 1.4 平面代数
2 例
2.1 平面的なもつれ 2.2 テンパリー – リーブ 2.3 ホップ代数
3 部分因数平面代数
3.1 意味 3.2 例と結果 3.3 フーリエ変換と二重投影
4 参考文献
意味
平面代数の考え方は、標準的な不変量を図式的に公理化したものです。
平面的なもつれ(影付きの)平面タングルは、有限数の入力ディスク、1 つの出力ディスク、偶数を与える交差しない文字列のデータです。2 n
{ 2n}
、ディスクごとの間隔と 1 ⋆ { star }
-マークされたディスクごとの間隔。
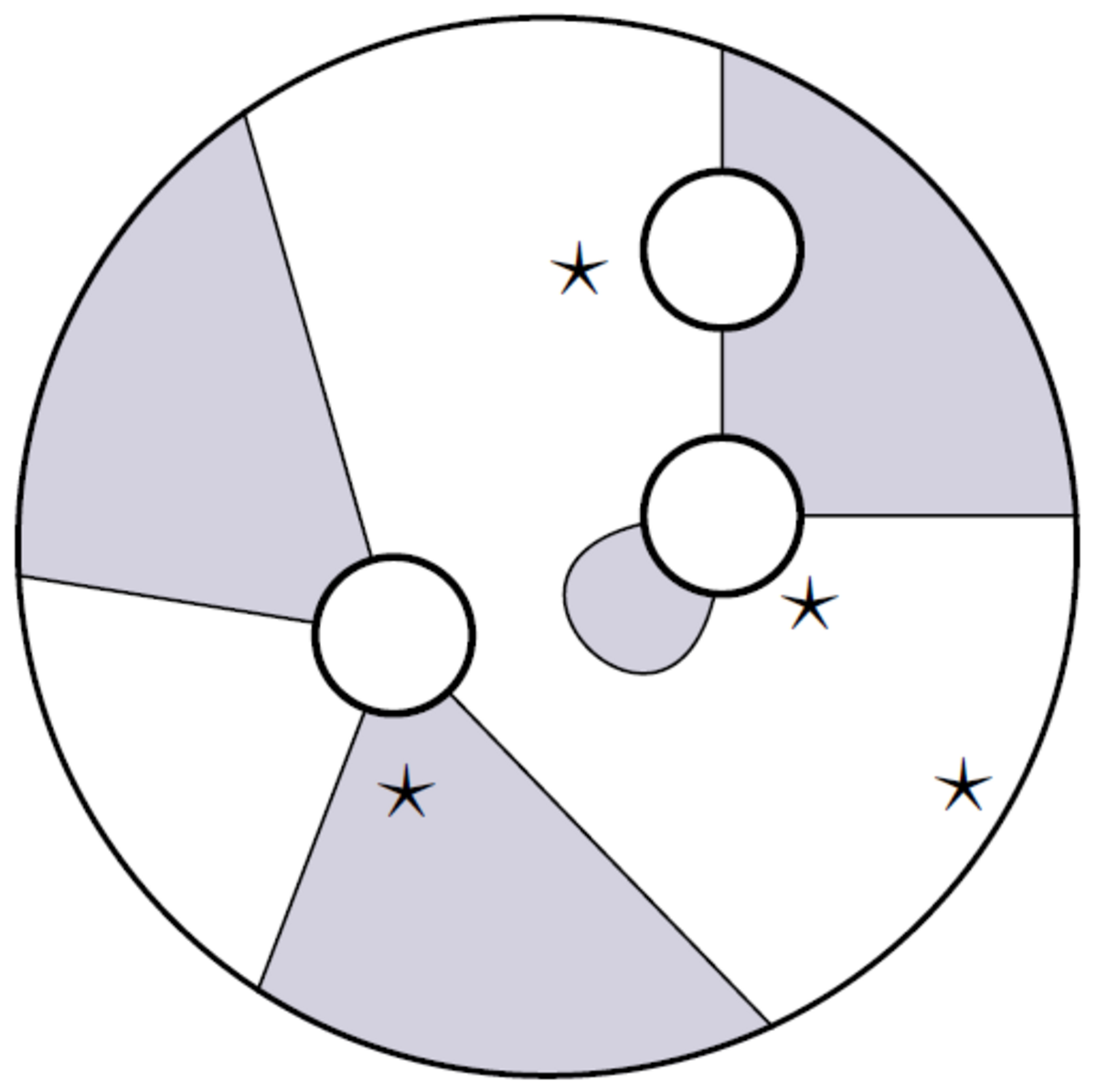
ここでは、マークは として表示されます。 ⋆ { star }
-形。各入力ディスクでは、2 つの隣接する発信文字列の間に配置され、出力ディスクでは、2 つの隣接する入力文字列の間に配置されます。平面もつれは同位体まで定義されます。
構成
2 つの平面タングルを構成するには、一方の出力ディスクをもう一方の入力に配置し、同じ数の間隔、マークされた間隔の陰影が同じになるようにします。 ⋆ { star }
-マークの間隔が一致します。最後に、一致する円を削除します。2 つの平面のもつれは、0、1、またはいくつかの可能な組成を持つ可能性があることに注意して
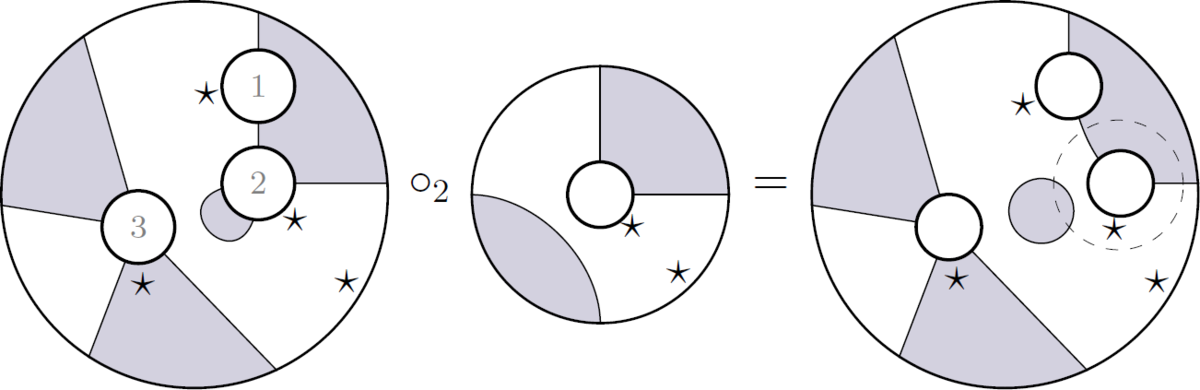
平面オペラド
平面オペラドは、そのような構成を持つすべての平面もつれ (同型まで) の集合です。
平面代数
平面代数は平面オペラドの表現です。より正確には、ベクトル空間のファミリーです。 ( P n ±) n ∈ N
{ ({mathcal {P}}_{n,pm })_{nin mathbb {N} }}
、と呼ばれる n { n}
-box スペース。平面オペラドが作用します。つまり、あらゆるもつれに対して作用します。 T { T}
(1 つの出力ディスクと r { r}
入力ディスク2 n 0
{ 2n_{0}}
と 2 n
1 … 2n r
{ 2n_{1},dots ,2n_{r}}
それぞれ間隔)多重線形マップがありますZ T : P n
1ϵ1 ⋯ ⊗ P n rϵ r P n 0ϵ ⋯0
{ Z_{T}:{mathcal {P}}_{n_{1},epsilon _{1}}otimes cdots otimes {mathcal {P}}_{n_{r}, epsilon _{r}}to {mathcal {P}}_{n_{0},epsilon _{0}}}
と ϵ I
∈ { + − } { epsilon _{i}in {+,-}}
の陰影に応じて ⋆ { star }
-マークされた間隔、およびこれらのマップ (パーティション関数とも呼ばれる) は、以下のすべての図が交換されるような方法でタングルの構成を尊重します。
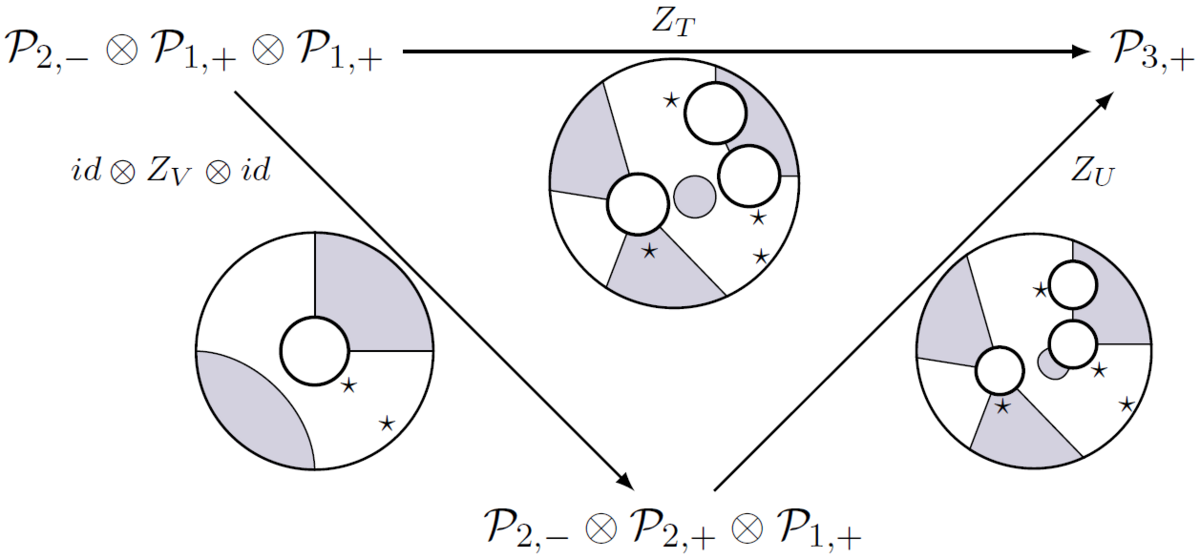
例
平面的なもつれ
ベクトル空間のファミリー ( T n ±) n ∈ N
{ ({mathcal {T}}_{n,pm })_{nin mathbb {N} }}
平面的なもつれによって生成される2 n
{ 2n}
出力ディスク上の間隔と白 (または黒) ⋆ { star }
-マーク区間。平面代数構造が認められます。
テンパリー – リーブ
テンパリー・リーブ平面代数
T L ( δ ) { {mathcal {TL}}(delta )}
入力ディスクなしの平面もつれによって生成されます。 3
{ 3}
-ボックススペースT L
3 +( δ ) { {mathcal {TL}}_{3,+}(delta )}
によって生成されます

さらに、閉じた文字列は次の乗算に置き換えられます。 δ { delta }
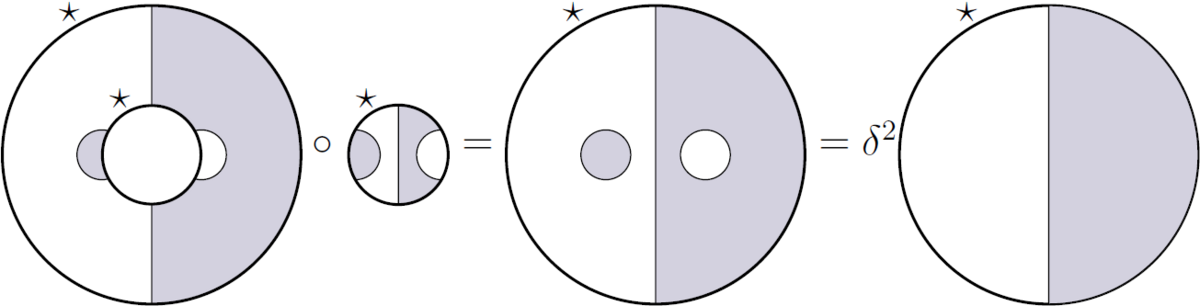
の寸法に注意してT L
n ±( δ ) { {mathcal {TL}}_{n,pm }(delta )}
カタルーニャ語の数字です1 n + 1( 2n n )
{ {frac {1}{n+1}}{binom {2n}{n}}}
。この平面代数は、テンパリー・リーブ代数の概念をコード化しています。
ホップ代数
代数的に閉じた体上の半単純および共半単純ホップ代数は、生成子と関係によって定義される平面代数にエンコードされ、非ゼロ係数を持つ接続された既約球面の非縮退平面代数に (同型まで) 「対応」します。 δ { delta }
そして深さは2です。
接続されたという意味に注意してください
薄暗い ( P 0 ±)= 1
{ dim({mathcal {P}}_{0,pm })=1}
(評価可能なものについては下記)、還元不可能な手段
薄暗い ( P 1 +)= 1
{ dim({mathcal {P}}_{1,+})=1}
、球状は以下で定義され、非縮退はトレース (以下で定義) が非縮退であることを意味します。
部分因数平面代数編集
意味
部分因子平面代数は平面です。 ⋆ { star }
-代数 ( P n ±) n ∈ N
{ ({mathcal {P}}_{n,pm })_{nin mathbb {N} }}
それは:(1) 有限次元:
薄暗い ( P n ±) < ∞
{ dim({mathcal {P}}_{n,pm })(2) 評価可能: P 0 ±= C
{ {mathcal {P}}_{0,pm }=mathbb {C} }
(3) 球状:t r
:=t r r = t r I
{ tr:=tr_{r}=tr_{l}}
(4) ポジティブ: ⟨ ある| b ⟩ = t r( b ⋆ ある ) { langle avert brangle =tr(b^{star }a)}
内積を定義します。(2) と (3) により、閉じた文字列 (網掛けの有無にかかわらず) は同じ定数としてカウントされることに注意して δ { delta }
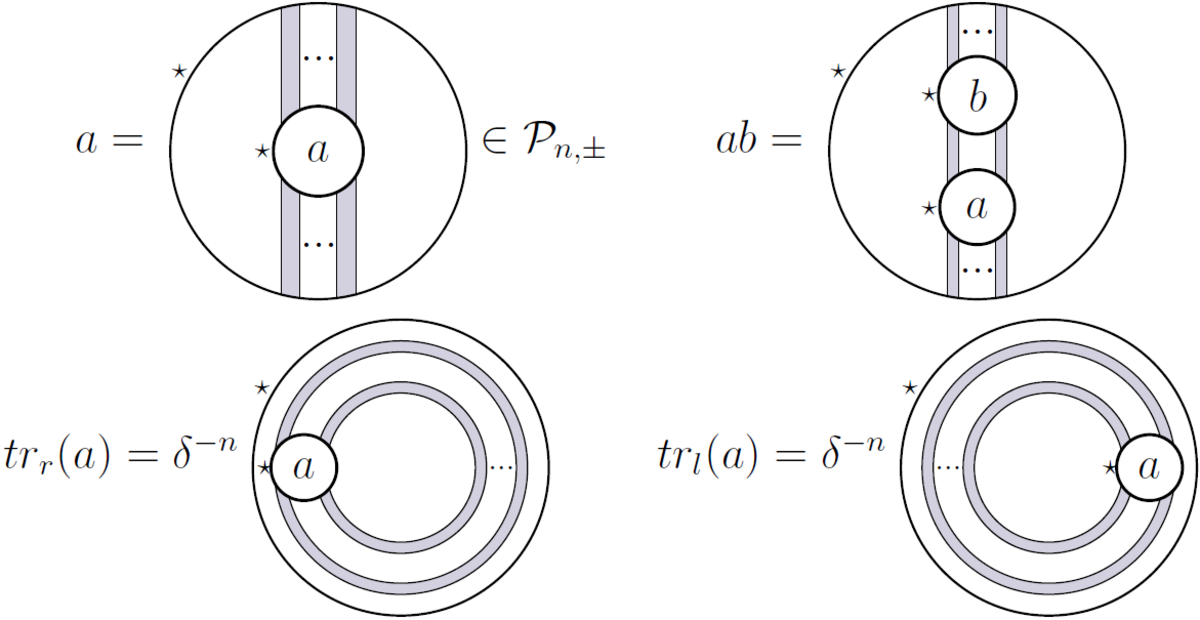
tangle アクションは、次のようにして随伴物を処理します。Z T( ある1 ⊗
ある2 ⊗ ⋯ ⊗
あるr ) ⋆ = Z T ⋆( ある1 ⋆ ⊗
ある2 ⋆ ⊗ ⋯ ⊗
あるr ⋆ )
{ Z_{T}(a_{1}otimes a_{2}otimes cdots otimes a_{r})^{star }=Z_{T^{star }}(a_{1}^ {star }otimes a_{2}^{star }otimes cdots otimes a_{r}^{star })}
と T ⋆
{ T^{star }}
の鏡像 T { T}
と あるI ⋆
{ a_{i}^{star }}
の随伴物
ある I { a_{i}}
P n 私 ϵ I { {mathcal {P}}_{n_{i},epsilon _{i}}}
例と結果
ノーゴースト定理: 平面代数
T L ( δ ) { {mathcal {TL}}(delta )}
ゴースト(つまり要素)がありません
ある
{ a}
と ⟨
ある | ある⟩ < 0
{ langle avert arangle <0}
) もし、そしてその場合に限りδ ∈ { 2
コス( π / n) |
n = 3 4 5
、 。 } ∪ [ 2 +∞ 】
{ delta in {2cos(pi /n)|n=3,4,5,…}cup }
ために δ { delta }
上記のように、 I { {mathcal {I}}}
ヌル理想値 (要素によって生成される) であること
ある
{ a}
と ⟨
ある | ある⟩ = 0
{ langle avert arangle =0}
)。それから商
T L ( δ) / I
{ {mathcal {TL}}(delta )/{mathcal {I}}}
は、テンパリー・リーブ・ジョーンズ部分因子平面代数と呼ばれる部分因子平面代数です。T L J( δ ) { {mathcal {TLJ}}(delta )}
。定数を含む任意の部分因数平面代数 δ { delta }
認める TL J ( δ ) { {mathcal {TLJ}}(delta )}
平面部分代数として。
平面代数 ( P n ±)
{ ({mathcal {P}}_{n,pm })}
極値サブ因子の標準不変量である場合に限り、サブ因子平面代数です。N ⊆ M
{ Nsubseteq M}
インデックスの
[ M: N 】 = δ 2
{ =delta ^{2}}
、 と P n +=N 』 ∩ M n − 1
{ {mathcal {P}}_{n,+}=N’cap M_{n-1}}
と P
n −=M 』 ∩ M n
{ {mathcal {P}}_{n,-}=M’cap M_{n}}
。 有限の深さまたは既約部分因子は極値です ( tr N 』 = t r M
{ tr_{N’}=tr_{M}}
の上N 』 ∩ M
{ N’cap M}
)。 任意の有限群 (より一般的には、任意の有限次元ホップ)をコード化する部分因数平面代数がC ⋆
{ {rm {C}}^{star }}
-algebra、Kac 代数と呼ばれます)、生成子と関係によって定義されます。(有限次元) Kac 代数は、深さ 2 の既約部分因子平面代数に (同型写像まで) 「対応」します。
有限群の包含に関連付けられた部分因子平面代数 は、 (コアのない) 包含を常に記憶しているわけではありません。
Bisch-Jones 部分因数平面代数
B J ( δ
1 δ 2) { {mathcal {BJ}}(delta _{1},delta _{2})}
(Fuss-Catalan とも呼ばれます) は次のように定義されます。 TL J ( δ ) { {mathcal {TLJ}}(delta )}
ただし、独自の定数を持つ 2 色の文字列を許可することにより、δ 1
{ delta _{1}}
と δ 2
{ delta _{2}}
、 とδ I
{ delta _{i}}
上記のように。これは、次のような中間体を持つ任意の部分因数平面代数の平面部分代数です。
[ K: N 】 =
δ1 2
{ =デルタ _{1}^{2}}
と [ M: K 】 =
δ2 2
{ =デルタ _{2}^{2}}
。 最初の有限深さの指数の平面代数δ 2> 4
{ delta ^{2}>4}
4}””>
はHaagerup部分因子平面代数と呼ばれます。インデックス付き( 5+ 13) / 2 〜 4.303
{ (5+{sqrt {13}})/2sim 4.303}
部分因子平面代数は、最大でもインデックスに関して完全に分類されます 5 { 5}
そしてその少し先。この分類はUffe Haagerupによって始められました。これは、(とりわけ)可能な主グラフのリストを、埋め込み定理およびクラゲ アルゴリズムとともに使用します。
サブ因子平面代数は、サブ因子が適用可能であれば、そのサブ因子を記憶します (つまり、その標準不変式が完全である)。有限の深さの超有限サブ因子は適用可能です。
適用できないケースについて: 指数 6 には分類不可能なほど多くの既約超有限部分因子があり、それらはすべて同じ標準不変量を持ちます。
フーリエ変換と二重投影
させてN ⊂ M
{ Nsubset M}
有限のインデックスサブファクターであること、および P { {mathcal {P}}}
対応するサブ因子平面代数。と仮定する P { {mathcal {P}}}
は既約です(すなわち、 P 1 +=N 』 ∩ M1 C
{ {mathcal {P}}_{1,+}=N’cap M_{1}=mathbb {C} }
)。させてN ⊂ K ⊂ M
{ Nサブセット Kサブセット M}
中間のサブファクターになります。ジョーンズ投影してみましょうe K M
:L 2 M ) L 2 K )
{ e_{K}^{M}:L^{2}(M)to L^{2}(K)}
。ご了承くださいe K M
∈ P 2 +
{ e_{K}^{M}in {mathcal {P}}_{2,+}}
。させてI d
:=e M M
{ id:=e_{M}^{M}}
と e 1 = e N M
{ e_{1}:=e_{N}^{M}}
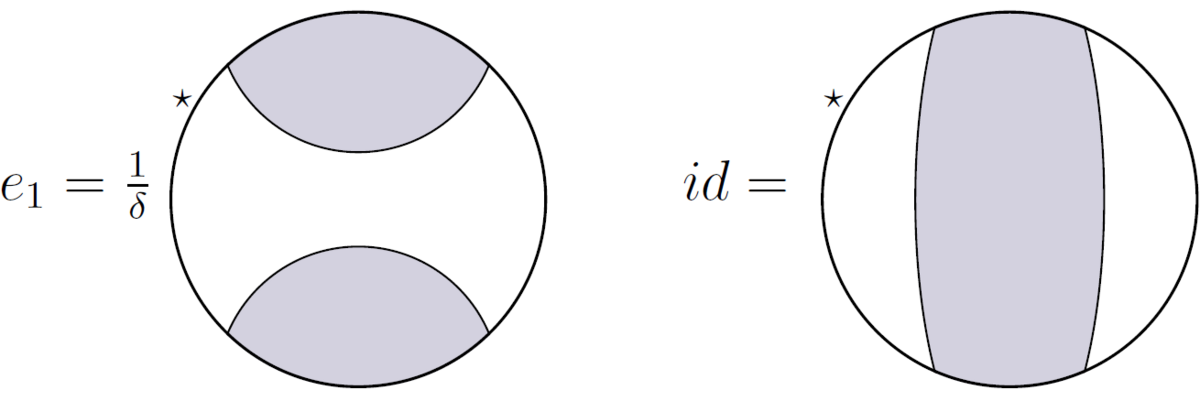
ご了承くださいt r( e1) = δ
−2
[ M: N 】 − 1
{ tr(e_{1})=delta ^{-2}=^{-1}}
と t r( Id ) = 1
{ tr(id)=1}
全単射線形マップを作成しましょう P 2 ± P 2 ∓
{ {mathcal {F}}:{mathcal {P}}_{2,pm }to {mathcal {P}}_{2,mp }}
フーリエ変換とも呼ばれます。 1 {表示スタイル 1}
(外側の星の) をクリックするか、90 ○
{ 90^{circ }}
回転; そしてさせてください
ある∗ b
{ a*b}
~の共積となる
ある
{ a}
と b
{ b}

余積という言葉は畳み込み積の短縮形であることに注意してそれは二項演算です。
余積は次の等式を満たす
ある∗ b = F F − 1( ある) F − 1 b )
) { a*b={mathcal {F}}({mathcal {F}}^{-1}(a){mathcal {F}}^{-1}(b)).}
正の演算子の場合
ある b
{表示スタイル a,b}
、共積
ある∗ b
{ a*b}
もポジティブです。これは図式的に見ることができます:

させてる  ̄ = F F( ある) )
{ {overline {a}}:={mathcal {F}}({mathcal {F}}(a))}
反逆的になる
ある
{ a}
(とも呼ばれている180 ○
{ 180^{circ }}
回転)。地図F 4
{ {mathcal {F}}^{4}}
4つに相当する 1 {表示スタイル 1}
– 外側の星をクリックすると、それが恒等マップになります。
ある ̄  ̄ = ある
{ {overline {overline {a}}}=a}
Kac 代数の場合、反接体は正確に対蹠体であり、有限群の場合は逆体に対応します 。
二重投影は投影ですb ∈ P
2 +
∖{ 0 }
{ bin {mathcal {P}}_{2,+}setminus {0}}
と F b )
{ {mathcal {F}}(b)}
投影の倍数。ご了承くださいe1 e N M
{ e_{1}=e_{N}^{M}}
と I d = e M M
{ id=e_{M}^{M}}
は二重投影です。これは次のように見ることができます。
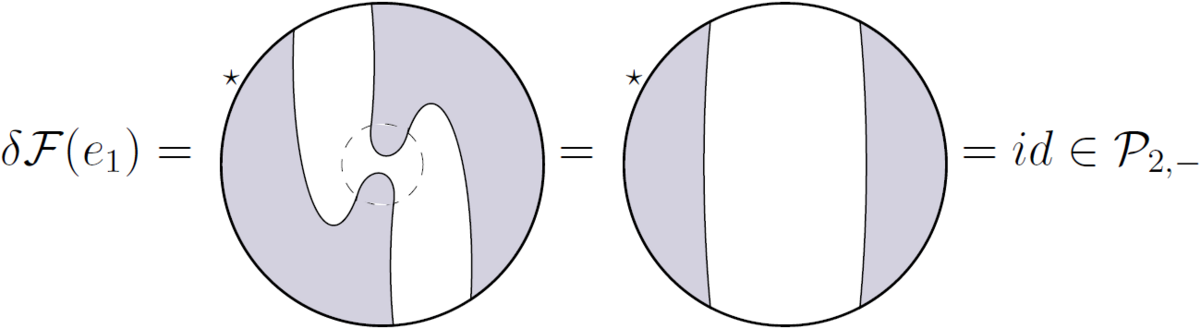
影 b
{ b}
ジョーンズ投影であれば二重投影ですe K M
{ e_{K}^{M}}
中間サブファクターのN ⊂ K ⊂ M
{ Nサブセット Kサブセット M}
, もしもe1 b = b  ̄=λ b ∗
b と λ −1 δ t r( b ) { e_{1}leq b={overline {b}}=lambda b*b,{text{ with }}lambda ^{-1}=delta tr(b)}
。 ガロア対応: Kac 代数の場合、双射影は左のコイデアル部分代数と 1-1 であり、有限群の場合、部分群に対応します。
既約部分因子平面代数の場合、双射影の集合は次の形式の有限格子です。 [ e 1 私d 】
{ }
、有限群の区間については
[ H G 】 { }
双射影を使用すると、中間部分因子の平面代数を作成できます。
不確定性原理は、既約部分因子平面代数にまで拡張されます。 P { {mathcal {P}}}
: させて
SX ) = T r( R(X ) )
{ {mathcal {S}}(x)=Tr(R(x))}
と R (X )
{ R(x)}
の範囲投影X
{ x}
と T r
{ Tr}
正規化されていないトレース (すなわち、T r = δ n
t r { Tr=delta ^{n}tr}
の上 P n ±
{ {mathcal {P}}_{n,pm }}
)。 非可換不確定性原理: LetX∈ P
2 ±
{ xin {mathcal {P}}_{2,pm }}
、ゼロ以外。それからS (X ) S( F(X ) ) ≥ δ 2
{ {mathcal {S}}(x){mathcal {S}}({mathcal {F}}(x))geq delta ^{2}}
仮定するとX
{ x}
と FX )
{ {mathcal {F}}(x)}
正の場合、等式は次の場合にのみ成立します。X
{ x}
は二重投影です。より一般的には、次の場合にのみ等式が成り立ちます。X
{ x}
は二重投影の二重シフトです。
参考文献
^ ヴォーン FR ジョーンズ(1999)、「平面代数、I」、arXiv : math/9909027
^ “Dror Bar-Natan: 出版物: コボルディズム” . Math.toronto.edu。土井:10.2140/gt.2005.9.1443。2016 年 11 月 20 日に取得。
^ バーナタン、ドロール (2005)。「もつれとコボディズムに関するホバノフのホモロジー」。ジオメトリとトポロジー。9 (3): 1443 ~ 1499 年。arXiv : math/0410495。土井:10.2140/gt.2005.9.1443。S2CID 1247623。
^ ヴォーン FR ジョーンズ(2017)、「トンプソンのグループ F および T のいくつかの単一表現」、J. Comb. 代数、1 (1): 1–44、arXiv : 1412.7740、doi : 10.4171/JCA/1-1-1、MR 3589908、S2CID 119631229
^ Vijay Kodiyalam、VS Sunder (2004)、「ジョーンズの平面代数について」、J. ノット理論の影響、13 (2): 219–247、doi : 10.1142/S021821650400310X、MR 2047470
^ “”Vijay Kodiyalam – 平面代数 – IMSc 2015″” . youtube.com。2015年11月14日。
^ Vijay Kodiyalam、VS Sunder (2006)、「半単純および共半単純ホップ代数の平面代数」、Proc. インドのアカド。科学。算数。科学。、116 (4): 1–16、arXiv : math/0506153、Bibcode : 2005math……6153K
^ Sorin Popa (1995)、「サブ因子の高次相対可換項の格子の公理化」、Inventiones Mathematicae、120 (3): 427–445、Bibcode : 1995InMat.120..427P、doi : 10.1007/BF01241137、MR 1334479、S2CID 1740471
^ アリス・ギオネ、ヴォーン・FR・ジョーンズ、ディミトリ・シュリャクテンコ (2010)、「ランダム行列、自由確率、平面代数および部分因子」、Clay Math。手順 、{11} : 201–239、MR 2732052
^ Vijay Kodiyalam、VS Sunder (2009)、「部分因子平面代数から部分因子へ」、Internat。J.Math.、20 (10): 1207–1231、arXiv : 0807.3704、doi : 10.1142/S0129167X0900573X、MR 2574313、S2CID 115161031
^ Paramita Das、Vijay Kodiyalam (2005)、「平面代数とオクネアヌ・シャマンスキーの定理」、Proc. アメール。算数。社会 、133 (9): 2751–2759、土井: 10.1090/S0002-9939-05-07789-0、ISSN 0002-9939、MR 2146224
^ Vijay Kodiyalam、Zeph Landau、VS Sunder (2003)、「Kac 代数に関連付けられた平面代数」、Proc. インドのアカド。科学。算数。科学。、113 (1): 15–51、土井: 10.1007/BF02829677、ISSN 0253-4142、MR 1971553、S2CID 56571515
^ Ved Prakash Gupta (2008)、「部分群-部分因子の平面代数」、数理科学論文集、118 (4): 583–612、arXiv : 0806.1791、Bibcode : 2008arXiv0806.1791G、doi : 10.1007/s120 44-008-0046 -0、S2CID 5589336
^ Vijay Kodiyalam、VS Sunder (2000)、「The subgroup-subfactor」、Math。スキャン。、86 (1): 45–74、土井: 10.7146/math.scand.a-14281、ISSN 0025-5521、MR 1738515
^ 泉正樹 (2002)、「同型グループサブグループサブ因子の特性評価」、Int. 算数。解像度 いいえ。、2002 (34): 1791–1803、土井: 10.1155/S107379280220402X、ISSN 1073-7928、MR 1920326
^ Dietmar Bisch、Vaughan Jones (1997)、「中間サブ因子に関連付けられた代数」、Inventiones Mathematicae、128 (1): 89–157、Bibcode : 1997InMat.128…89J、doi : 10.1007/s002220050137、S2CID 11937264 0
^ Pinhas Grossman、Vaughan Jones (2007)、「余分な構造を持たない中間サブ因子」、J. Amer. 算数。社会 、20 (1): 219–265、Bibcode : 2007JAMS…20..219G、doi : 10.1090/S0894-0347-06-00531-5、MR 2257402
^ Emily Peters (2010)、「Haagerup 部分因子の平面代数構築」、Internat。J.Math.、21 (8): 987–1045、arXiv : 0902.1294、doi : 10.1142/S0129167X10006380、MR 2679382、S2CID 951475
^ Vaughan FR Jones、Scott Morrison、Noah Snyder (2014)、「最大指数のサブファクターの分類」 5 { 5}
“”、Bull. Amer. Math. Soc. (NS)、51 (2): 277–327、arXiv : 1304.6141、doi : 10.1090/S0273-0979-2013-01442-3、MR 3166042、S2CID 29962597
^ Narjess Afzaly、Scott Morrison、David Penneys (2015)、最大インデックスによるサブ因子の分類
5+ 1 / 4
{ 5+1/4}
、70ページ、arXiv : 1509.00038、Bibcode : 2015arXiv150900038A
^ Uffe Haagerup (1994)、「指数範囲内のサブファクターの主なグラフ」4 <
[ M: N 】 < 3 + 2
{ 4<<3+{sqrt {2}}}
“、サブファクター (久世草、1993) : 1–38、MR 1317352
^ Vaughan Jones、David Penneys (2011)、「有限深さサブ因子平面代数の埋め込み定理」、Quantum Topol。、2 (3): 301–337、arXiv : 1007.3173、doi : 10.4171/QT/23、MR 2812459、S2CID 59578009
^ Stephen Bigelow、David Penneys (2014)、「主なグラフの安定性とクラゲ アルゴリズム。」、Math。アン。、358 (1–2): 1–24、arXiv : 1208.1564、doi : 10.1007/s00208-013-0941-2、MR 3157990、S2CID 3549669
^ Popa、Sorin (1994)、「タイプ II の従順なサブ因子の分類」、Acta Mathematica、172 (2): 163–255、doi : 10.1007/BF02392646、MR 1278111
^ Arnaud Brothier、Stefaan Vaes (2015)、「同じ標準不変量と所定の基本群を持つ超有限部分因子の族。」、J. Noncommut. ゲム。、9 (3): 775–796、arXiv : 1309.5354、doi : 10.4171/JNCG/207、MR 3420531、S2CID 117853753
^ Zhengwei Liu (2016)、「小ランクの交換関係平面代数」、Trans。アメール。算数。社会 、368 (12): 8303–8348、arXiv : 1308.5656、doi : 10.1090/tran/6582、ISSN 0002-9947、MR 3551573、S2CID 117030298
^ Dietmar Bisch (1994)、「中間サブ因子に関するメモ」、Pacific J. Math. 、163 (2): 201–216、土井: 10.2140/pjm.1994.163.201、ISSN 0030-8730、MR 1262294
^ Zeph A. Landau (2002)、「交換関係平面代数」、Geom. デディカタ、95 : 183–214、doi : 10.1023/A:1021296230310、ISSN 0046-5755、MR 1950890、S2CID 119036175
^ 泉正樹、Roberto Longo、Sorin Popa (1998)、「Kac 代数への一般化を伴うフォン ノイマン代数の自己同型のコンパクトな群に対するガロア対応」、J. Funct. アナル。、155 (1): 25–63、arXiv : funct-an/9604004、doi : 10.1006/jfan.1997.3228、ISSN 0022-1236、MR 1622812、S2CID 12990106
^ 綿谷康夫 (1996)、「中間サブ因子の格子」、J. Funct. アナル。、140 (2): 312–334、doi : 10.1006/jfan.1996.0110、hdl : 2115/68899、ISSN 0022-1236、MR 1409040
^ Zeph A. Landau (1998)、「Intermediate subfactors」、論文 – カリフォルニア大学バークレー校: 132pp
^ Keshab Chandra Bakshi (2016)、「Intermediate planar algebra revisited」、International Journal of Mathematics、29 (12): 31pp、arXiv : 1611.05811、Bibcode : 2016arXiv161105811B、doi : 10.1142/S0129167X18 500775 、S2CID 119305436
^ Chunlan Jiang、Zhengwei Liu、Jinsong Wu (2016)、「非可換不確定性原理」、J. Funct. アナル。、270 (1): 264–311、arXiv : 1408.1165、doi : 10.1016/j.jfa.2015.08.007、S2CID 16295570 “
