平面グラフ – 日本語百科事典辞書

Planar_graph

「三角グラフ」完全なグラフの折れ線グラフについては、「折れ線グラフ § 非常に規則的で完全な折れ線グラフ」を参照して三角グラフについては、「Chordal グラフ」を参照して3 つの変数にわたってプロットされたデータグラフについては、「三値プロット」を参照して
グラフの例
平面
非平面的
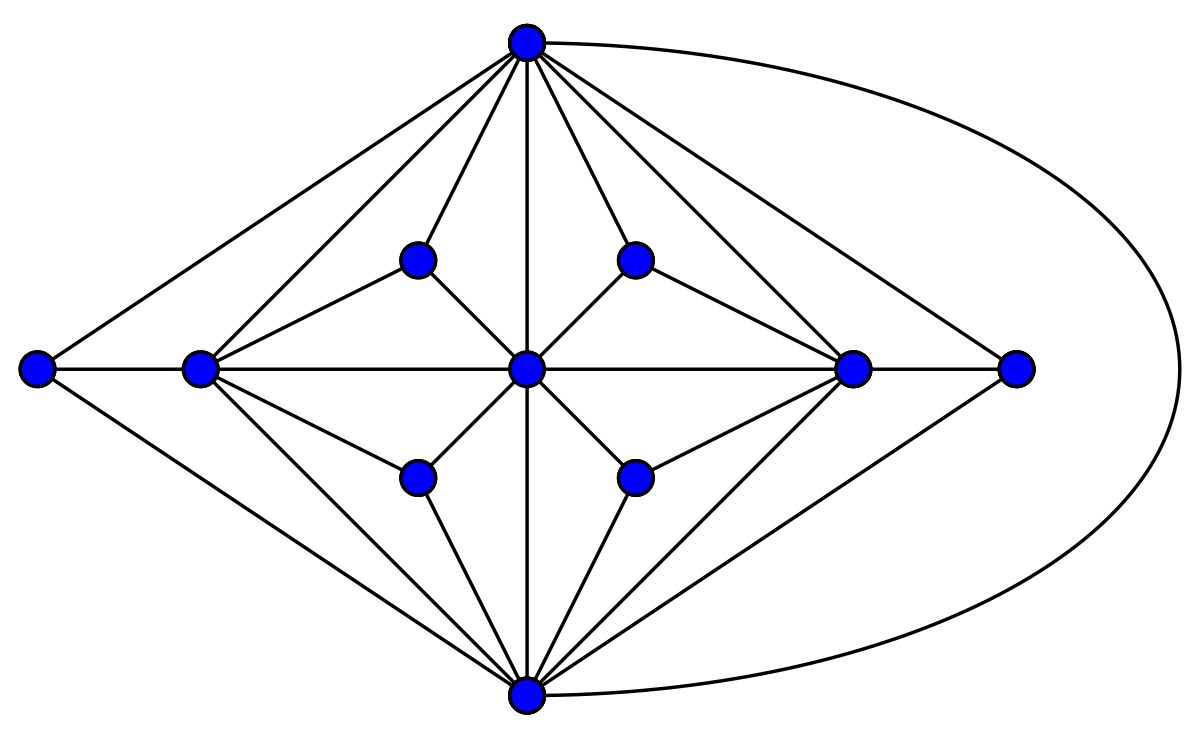
バタフライグラフ
完全なグラフ K 5
完全なグラフ K 4 ユーティリティグラフ K 3，3
グラフ理論では、平面グラフは平面に埋め込むことができるグラフです。つまり、エッジが端点でのみ交差するように平面上に描画できます。つまり、エッジが交差しないように描画できます。このような図は、平面グラフまたはグラフの平面埋め込みと呼ばれます。平面グラフは、すべてのノードから平面上の点へ、およびすべてのエッジから平面曲線へのマッピングを含む平面グラフとして定義できます。その平面上では、各曲線の極点がその終点ノードからマッピングされた点となり、すべての曲線は極点を除いて互いに素になります。
平面上に描画できるすべてのグラフは、立体投影を使用して球体上にも描画でき、その逆も同様です。
平面グラフは、組み合わせマップまたは回転システムによってエンコードできます。
通常、地峡が存在しないなどの追加の仮定を伴う、球面上のトポロジー的に等価な描画の等価クラスは、平面マップと呼ばれます。平面グラフには外部または境界のない面がありますが、平面マップのどの面も特定のステータスを持ちません。
平面グラフは、特定の属の表面上に描画可能なグラフに一般化されます。この用語では、平面 (および球) が属数0 の表面であるため、平面グラフは属数 0 を持ちます。他の関連トピックについては、「グラフの埋め込み」を参照して

コンテンツ
1 平面性の基準
1.1 クラトフスキーとワーグナーの定理 1.2 その他の基準
2 プロパティ
2.1 オイラーの公式 2.2 平均程度 2.3 コイングラフ 2.4 平面グラフ密度 2.5 デュアルグラフ
3 平面グラフのファミリー
3.1 最大平面グラフ 3.2 外側平面グラフ 3.3 ヘイリングラフ 3.4 上向きの平面グラフ 3.5 凸型平面グラフ 3.6 単語で表現可能な平面グラフ
4 定理
4.1 平面グラフの列挙 4.2 その他の結果
5 一般化
6 こちらも参照
7 ノート
8 参考文献
9 外部リンク

平面性の基準

クラトフスキーとワーグナーの定理

クラトフスキーまたはワグナーの定理を使用し、 K 5 (上) またはK 3，3 (下)の部分グラフを見つけることで、超立方体グラフが非平面であることを言葉なしで証明します。
ポーランドの数学者カジミェシュ・クラトフスキは、現在クラトフスキーの定理として知られている禁断グラフの観点から平面グラフの特徴を示しました。
有限グラフは、完全なグラフK 5または完全な 2 部グラフK 3，3 (ユーティリティグラフ)の細分である部分グラフを含まない場合に限り、平面的です。
グラフの細分化は、頂点をエッジに挿入する (たとえば、エッジを0 回以上変更する) ことによって行われます。

K 5またはK 3，3サブグラフのないグラフの例。ただし、K 3，3のサブディビジョンが含まれているため、非平面的になります。
ワーグナーの定理は、細分割を考慮する代わりに、マイナーを扱います。
有限グラフは、マイナーとしてK 5またはK 3，3
を持たない場合にのみ平面的です。
グラフのマイナーは、サブグラフを取得し、元の終端頂点の各隣接点が新しい頂点の隣接点になるように、エッジを頂点に繰り返し縮小することによって得られます。

Petersen グラフにはK 3，3グラフと若干の同型が含まれており、したがって非平面であることを
示すアニメーション
クラウス・ワグナーは、より一般的に、グラフのマイナー閉クラスが「禁止されたマイナー」の有限集合によって決定されるかどうかを尋ねました。これは現在ではロバートソン・シーモアの定理であり、長い一連の論文で証明されています。この定理の言葉では、K 5とK 3，3は有限平面グラフのクラスの禁止されたマイナーです。

その他の基準
実際には、Kuratowski の基準を使用して、特定のグラフが平面であるかどうかを迅速に判断することは困難です。ただし、この問題には高速アルゴリズムが存在します。n 個の頂点を持つグラフの場合、グラフが平面であるかどうかを時間O ( n ) (線形時間)で判断することができます(平面性テストを参照)。
v個の頂点、e個のエッジ、およびf個の面を持つ単純な接続された平面グラフの場合、 v ≥ 3に対して次の単純な条件が当てはまります。
定理 1. e ≤ 3 v – 6 ;
定理 2. 長さ 3 のサイクルが存在しない場合、e ≤ 2 v – 4になります。
定理 3. f ≤ 2 v – 4。
この意味で、平面グラフは、最大O ( v 2 )より漸近的に小さいO ( v )エッジのみを持つという点で、まばらなグラフです。たとえば、グラフK 3，3には、6 つの頂点、9 つのエッジがあり、長さ 3 のサイクルはありません。したがって、定理 2 により、グラフは平面であることはできません。これらの定理は、平面性の必要条件を提供しますが、十分条件ではないため、グラフが平面ではなく、平面であることを証明するためにのみ使用できます。定理 1 と定理 2 の両方が満たされない場合は、他の方法が使用される可能性が
ホイットニーの平面性基準は、代数双対の存在に基づいて特徴付けを行います。
マクレーンの平面性基準は、サイクル空間を介して有限平面グラフの代数的特徴付けを与えます。
Fraysseix -Rosenstiehl の平面性基準は、深さ優先探索木の共木エッジの 2 分割の存在に基づいて特徴付けを行います。これは、左右の平面性テストアルゴリズムの中心となります。
シュナイダーの定理は、半次次元の観点から平面性を特徴づけます。
Colin de Verdière の平面性基準は、グラフで定義された特定のシュレーディンガー演算子の第 2 固有値の最大多重度に基づいて特性を示します。
Hanani -Tutte の定理は、独立したエッジの各ペアが偶数回交差する描画がある場合に限り、グラフは平面であると述べています。これは、2 を法とする連立方程式を介して平面グラフを特徴付けるために使用できます。

プロパティ

オイラーの公式
詳細は「オイラー特性 § 平面グラフ」を参照
オイラーの公式によれば、有限の接続された平面グラフがエッジの交差なしで平面に描画され、vは頂点の数、eはエッジの数、fは面 (エッジによって境界付けられた領域を含む領域) の数になります。外側の無限に大きな領域)、その後v − e + f = 2.
{ v-e+f=2.}

例として、上記のバタフライグラフでは、 v = 5、e = 6、およびf = 3です。一般に、このプロパティがf面のすべての平面グラフに当てはまる場合、グラフの平面を維持しながら追加の面を作成するグラフへの変更は、v – e + fを不変に保ちます。この性質はf = 2のすべてのグラフに当てはまるため、数学的帰納法により、すべての場合に当てはまります。オイラーの公式は次のように証明することもできます。グラフがツリーでない場合は、サイクルを完了するエッジを削除します。これにより、 eとf の両方が1 ずつ減り、 v – e + fは一定のままになります。残りのグラフがツリーになるまで繰り返します。ツリーにはv = e + 1およびf = 1があり、v – e + f = 2が得られます。つまり、オイラー特性は 2 です。
有限で接続された単純な平面グラフでは、すべての面 (おそらく外側の面を除く) は少なくとも 3 つのエッジで囲まれ、すべてのエッジは最大 2 つの面に接触します。オイラーの公式を使用すると、 v ≥ 3の場合、次の意味でこれらのグラフが疎であることがわかります。e ≤ 3 v − 6.
{ eleq 3v-6.}

凸多面体から平面グラフを形成する
正十二面体のシュレーゲル図。
オイラーの公式は凸多面体にも当てはまります。これは偶然ではありません。すべての凸多面体は、多面体のシュレーゲル図を使用することによって、接続された単純な平面グラフに変えることができます。これは、多面体の 1 つの中心付近を遠近の中心として選択した平面への多面体の透視投影です。多面体の面。すべての平面グラフがこのように凸多面体に対応するわけではありません。たとえば、木はそうではありません。シュタイニッツの定理によれば、凸多面体から形成される多面体グラフは、まさに有限の3 接続の単純な平面グラフです。より一般的には、オイラーの公式は、その凸面に関係なく、トポロジー的に球と同等の表面を形成する単純な多角形を面とする任意の多面体に適用されます。

平均程度
複数のエッジを持つ接続された平面グラフは、各面に少なくとも 3 つの面エッジ入射があり、各エッジが正確に 2 つの入射に寄与するため、不等式2 e ≥ 3 fに従います。この不等式をオイラーの公式v – e + f = 2で代数変換すると、有限平面グラフの平均次数は厳密に 6 未満であることがわかります。平均次数が高いグラフは平面ではあり得ません。

コイングラフ
詳細は「円パッキング定理」を参照

K − 5に関する円パッキング定理の例、5 つの頂点から 1 つのエッジを引いた完全なグラフ。
平面上に描かれた 2 つの円が正確に 1 点で交差するとき、それらは接している(または接している) と言います。「コイングラフ」は、各円に頂点を作成し、接している円の各ペアにエッジを作成することによって、重複する内部を持たない円のセットによって形成されるグラフです。1936 年にPaul Koebeによって初めて証明されたサークルパッキング定理は、グラフがコイングラフである場合にのみ平面であると述べています。
この結果は、すべての単純な平面グラフは、エッジが互いに交差しない直線セグメントになるように平面に埋め込むことができるというファーリの定理の簡単な証明を提供します。グラフの各頂点をコイングラフ表現の対応する円の中心に配置すると、キス円の中心間の線分は他の辺と交差しません。

平面グラフ密度
平面グラフまたはネットワークのメッシュ係数または密度Dは、境界面の数f – 1 ( Mac Lane の平面性基準によるグラフの回路ランクと同じ) とその最大可能値2 vの比です。 – v個の頂点を持つグラフの場合は5 😀 = f
−1 v − 5
{ D={frac {f-1}{2v-5}}}

密度は0 ≤ D ≤ 1に従い、完全に疎な平面グラフ (ツリー) の場合はD = 0 、完全に密な (最大) 平面グラフの場合はD = 1になります。

デュアルグラフ

平面グラフとその双対
エッジ交差のない平面内に (必ずしも単純ではない) 接続されたグラフの埋め込みGが与えられると、次のように双対グラフ G*を構築します。 Gの各面(外側の面を含む) と各エッジeに対して 1 つの頂点を選択します。 Gでは、eで交わるGの2 つの面に対応するG*の 2 つの頂点を接続する新しいエッジをG*に導入します。さらに、このエッジはe と1 回だけ交差し、GまたはG*の他のエッジと交差しないように描画されます。この場合、G*は再び (必ずしも単純ではない) 平面グラフの埋め込みになります。Gと同じ数のエッジがあり、Gと同じ数の面があり、 Gと同じ数の面が頂点を持っています。「双対」という用語は、 G ** = Gという事実によって正当化されます。ここでの等価性は、球上の埋め込みの等価性です。Gが凸多面体に対応する平面グラフである場合、 G*は双対多面体に対応する平面グラフです。
双対は、双対グラフの多くのプロパティが元のグラフのプロパティに簡単な方法で関連付けられており、双対グラフを調べることでグラフに関する結果を証明できるため便利です。
特定の埋め込みに対して構築された双対は一意 (同型まで) ですが、グラフには異なる (つまり、非同型) 埋め込みから得られた異なる (つまり、非同型) 双対が含まれる場合が
平面グラフのファミリー編集

最大平面グラフ

Goldner -Harary グラフは最大の平面的です。そのすべての面は 3 つのエッジで囲まれています。
単純なグラフが平面である場合、そのグラフは最大平面と呼ばれますが、(指定された頂点セット上に) エッジを追加すると、その特性が破壊されます。すべての面 (外側の面を含む) は 3 つのエッジによって境界付けされ、別の用語である平面三角形分割を説明します。別名「三角グラフ」または「三角グラフ」も使用されていますが、それぞれ完全なグラフの折れ線グラフと弦グラフを指すことが一般的であるため、曖昧です。すべての最大平面グラフは最小 3 接続です。
最大平面グラフにv > 2のv個の頂点がある場合、正確に3 v – 6 つのエッジと2 v – 4つの面が
アポロニアンネットワークは、三角形の面を 3 つの小さな三角形に繰り返し分割することによって形成される最大の平面グラフです。同等に、それらは平面3 ツリーです。
絞められたグラフは、すべての周辺サイクルが三角形であるグラフです。最大平面グラフ (より一般的には多面体グラフ) では、周辺サイクルが面であるため、最大平面グラフは絞殺されます。絞扼グラフには弦グラフも含まれており、まさに完全なグラフと最大平面グラフのクリークサム(エッジを削除せずに)によって形成できるグラフです。

外側平面グラフ
外側平面グラフは、すべての頂点が埋め込みの非境界面に属するような、平面内に埋め込みを含むグラフです。すべての外側平面グラフは平面ですが、その逆は当てはまりません。K 4は平面ですが、外側平面ではありません。Kuratowski の定理と同様の定理は、有限グラフがK 4またはK 2，3の部分を含まない場合にのみ、外側平面であると述べています。上記は、新しい頂点を追加して G から形成され、他のすべての頂点にエッジが接続されているグラフが平面グラフである場合、グラフ Gが外側平面であるという事実の直接の帰結です。
グラフの 1-outerplanar 埋め込みは、outerplanar 埋め込みと同じです。k > 1の場合、外面の頂点を削除すると( k – 1) -outerplanar 埋め込みになる場合、平面埋め込みはk -outerplanar になります。グラフにk -outerplanar の埋め込みがある場合、そのグラフはk -outerplanar です。

ヘイリングラフ
Halin グラフは、ツリーの平面埋め込みによって与えられる順序で、葉をサイクルに接続することによって、無向平面ツリー (次数 2 ノードを持たない) から形成されるグラフです。同様に、これは1 つの面が他のすべての面に隣接する多面体グラフです。すべての Halin グラフは平面です。外部平面グラフと同様に、Halin グラフのツリー幅は狭いため、制限のない平面グラフよりも多くのアルゴリズムの問題が解決されやすくなります。

上向きの平面グラフ
上向きの平面グラフは、常に上向きの非交差曲線としてエッジを持つ平面内に描画できる有向非巡回グラフです。すべての平面有向非循環グラフが上向き平面であるわけではないため、特定のグラフが上向き平面であるかどうかをテストするのはNP 完全です。

凸型平面グラフ
平面グラフは、そのすべての面 (外側の面を含む) が凸多角形である場合、凸であると言われます。すべての平面グラフが凸状の埋め込みを持っているわけではありません (たとえば、完全な 2 部グラフK 2，4 )。グラフを凸状に描画できる十分条件は、それが3 つの頂点で接続された平面グラフの細分化であることです。トゥッテのバネ定理では、単純な 3 つの頂点が接続された平面グラフの場合、内側の頂点の位置がその近傍の頂点の平均になるように選択できるとさえ述べています。

単語で表現可能な平面グラフ
単語で表現可能な平面グラフには、三角形のない平面グラフ、より一般的には 3 色可能な平面グラフ、三角グリッドグラフの特定の面の分割、、グリッドで覆われた円柱グラフの特定の三角形分割が含まれます。

定理

平面グラフの列挙(ラベル付き) 平面グラフの数の漸近線 n { n}

頂点はg ⋅ n − 7
/2 γ n
⋅n ！
{ gcdot n^{-7/2}cdot gamma ^{n}cdot n!}

、どこγ ≈ 27.22687
{ gamma およそ 27.22687}
と g ≈ 0.43 × 10 − 5
{ g約 0.43times 10^{-5}}
。ほぼすべての平面グラフには、指数関数的な数の自己同型性が
ラベルのない (非同型) 平面グラフの数 n { n}

頂点の間にある27.2 n
{ 27.2^{n}}
と 6月30日 n { 30.06^{n}}

。

その他の結果
4色定理は、すべての平面グラフは 4色可能(つまり 4 分割) であると述べています。
ファーリの定理は、すべての単純な平面グラフは平面直線グラフとして表現できると述べています。ユニバーサル点セットは、 n個の頂点を持つすべての平面グラフが点セット内のすべての頂点とそのような埋め込みを持つような点のセットです。整数格子の長方形のサブセットを取ることによって形成される、二次サイズの普遍点セットが存在します。すべての単純な外側平面グラフでは、すべての頂点が固定円上にあり、すべてのエッジが円盤の内側にあり交差しない直線セグメントであるような平面への埋め込みが許可されているため、n 頂点の正多角形は外側平面グラフにとって普遍的です。
シャイナーマンの予想(現在は定理) は、すべての平面グラフは平面内の線分の交差グラフとして表すことができると述べています。
平面セパレータ定理では、すべてのn頂点平面グラフは、O( √ n ) 個の頂点を削除することで最大 2 n /3 のサイズの 2 つのサブグラフに分割できると述べています。結果として、平面グラフもツリー幅と枝幅O( √ n ) を持ちます。
平面積構造定理は、すべての平面グラフは、ツリー幅が最大 8 のグラフとパスの強力なグラフ積の部分グラフであると述べています。この結果は、平面グラフが有界のキュー数、有界の非反復色彩数、およびほぼ線形サイズの普遍的なグラフを持つことを示すために使用されています。また、頂点ランキングや平面グラフのp中心色付けにも応用できます。
v個の頂点を持つ 2 つの平面グラフの場合、それらが同型であるかどうかを時間 O( v )で判断することができます(グラフ同型問題も参照)。

一般化
アペックスグラフは、 1 つの頂点を削除することで平面化できるグラフであり、kアペックスグラフは、最大でk個の頂点を削除することによって平面化できるグラフです。
1平面グラフは、エッジごとに最大 1 つの単純な交差で平面内に描画できるグラフであり、k平面グラフは、エッジごとに最大でk 個の単純な交差で描画できるグラフです。
マップグラフは、2 つの領域が少なくとも 1 つの境界点を共有する場合にそれらの領域を接続することによって、平面内で単純に接続された有限個の内部独立領域の集合から形成されるグラフです。最大 3 つの領域が 1 つの点で交わる場合、結果は平面グラフになりますが、4 つ以上の領域が 1 つの点で交わる場合、結果は非平面になる可能性があります (たとえば、円を扇形に分割すると考えます。領域である場合、すべてのセクターが共通の境界点 (中心点) を持っているため、対応するマップグラフが完全なグラフになります。
トロイダルグラフは、トーラス上に交差せずに埋め込むことができるグラフです。より一般的には、グラフの属とは、グラフを埋め込むことができる 2 次元曲面の最小の属です。平面グラフには種数 0 があり、非平面トロイダルグラフには種数 1 がすべてのグラフは、交差することなく (方向付け可能で接続された) 閉じた 2 次元表面 (ハンドル付きの球) に埋め込むことができるため、グラフの種類は明確に定義されます。明らかに、グラフを種数 g の (方向付け可能な、接続された、閉じた) 曲面に交差せずに埋め込むことができる場合、それ以上の種数を持つすべての (方向付け可能な、接続された、閉じた) 曲面に交差せずに埋め込むことができます。グラフ理論には他にも、「X」という修飾語を付けて「X 属」と呼ばれる概念が一般に、これらは、修飾子のない上記で定義された「属」の概念とは異なります。特に、グラフの非方向付け可能な属 (その定義に方向付け不可能な表面を使用) は、一般的なグラフではそのグラフの属 (定義に方向付け可能な表面を使用) とは異なります。
どのグラフも交差することなく 3 次元空間に埋め込むことができます。実際、2 つの平面設定では、どのようなグラフも交差することなく描画できます。この設定では、2 つの平面が互いに重なり合い、エッジは任意の場所で一方の平面からもう一方の平面に「ジャンプ」および「ドロップダウン」できます。 (グラフの頂点だけでなく) エッジが他のエッジと交差するのを避けることができます。これは、両面回路基板を使用して、基板の側面間の電気接続を行うことができる任意の導電体ネットワークを作成することが可能であると解釈できます (典型的な現実の回路基板で可能であるように、電気接続が必要です)。基板の上面はワイヤ片によって実現され、下面は基板自体に構築された銅のトラックによって実現され、基板の側面間の電気接続は穴を開け、ワイヤを穴に通し、はんだ付けすることによって実現されます。線路の中へ）; これは、道路網を構築するには橋かトンネルだけが必要で、両方は必要ない（2 つのレベルで十分で、3 つのレベルは必要ない）と言っていると解釈することもできます。また、3 次元では、交差のないグラフを描くことに関する問題は簡単です。ただし、平面グラフの 3 次元類似物は、リンクなしで埋め込み可能なグラフ、つまり 2 つのサイクルがトポロジ的に互いにリンクされない方法で 3 次元空間に埋め込むことができるグラフによって提供されます。Kuratowski と Wagner が平面グラフをマイナーとしてK 5またはK 3，3を含まないグラフとして特徴付けたのと同様に、リンクレスで埋め込み可能なグラフは、マイナーとして次のいずれかを含まないグラフとして特徴付けることができます。Petersen ファミリーの 7 つのグラフ。外側の平面グラフと平面グラフが、コランドヴェルディエールグラフの不変性が最大 2 つまたは 3つあるグラフであるという特徴付けと同様に、リンクなしで埋め込み可能なグラフは、コランドヴェルディエールグラフの不変性が最大 4 つあるグラフです。

こちらも参照
組み合わせマップ平面グラフをエンコードできる組み合わせオブジェクト
平面化: 各交差点を新しい頂点に置き換えることにより、交差点を含む図面から形成された平面グラフ
厚さ (グラフ理論)、特定のグラフのエッジを分割できる平面グラフの最小数
Planarity、平面上に平面グラフを埋め込むことが目的のパズルコンピューターゲーム
Sprouts (ゲーム)、特定の制約を受ける平面グラフがゲームプレイの一部として構築される紙と鉛筆のゲーム
3つのユーティリティの問題、人気のパズル

ノート
^ トルドー、リチャード J. (1993)。グラフ理論入門(加筆増補再版)。ニューヨーク：ドーバーパブ。p. 64.ISBN _ 978-0-486-67870-2。2012 年8 月 8 日に取得。したがって、平面グラフは、平面上に描画される場合、エッジ交差がないか、エッジ交差なしで再描画できます。
^ Barthelemy、M. （2017)。「1.5 平面グラフ」。空間ネットワークの形態形成。スプリンガー。p. 6.ISBN _
978-3-319-20565-6。
^ ビュール、J. ゴートレー、J. ソール、RV; クンツ、P. バルベルデ、S. ドヌーブール、JL; Theraulaz， G. （2004)、「ギャラリーのアリネットワークにおける効率と堅牢性」、European Physical Journal B、42 (1): 123–129、Bibcode : 2004EPJB…42..123B、doi : 10.1140/epjb/ e2004-00364-9、S2CID 14975826
。
^ Schnyder， W. (1989)、「平面グラフとポセット次元」、Order、5 (4): 323–343、doi : 10.1007/BF00353652、MR 1010382、S2CID 122785359
。
^ バスカー、ジャヤラム; Sahni、Sartaj (1988)、「平面三角グラフの長方形双対を見つける線形アルゴリズム」、Algorithmica、3 (1–4): 247–278、doi : 10.1007/BF01762117、S2CID 2709057
。
^ シーモア、PD; Weaver、RW (1984)、「弦グラフの一般化」、Journal of Graph Theory、8 (2): 241–251、doi : 10.1002/jgt.3190080206、MR 0742878
。
^ Felsner、Stefan （2004)、「1.4 外側平面グラフと凸幾何グラフ」、幾何グラフと配置、数学の上級講義、Friedr. Vieweg & Sohn、ヴィースバーデン、6–7 ページ、土井: 10.1007/978-3-322-80303-0_1、ISBN
3-528-06972-4、MR 2061507
^ シスウォ、マチェイ M.; Proskurowski、Andrzej (1983)、「Halin グラフについて」、グラフ理論: 1981 年 2 月 10 ～ 13 日にポーランドのラグフで開催された会議の議事録、数学の講義ノート、vol. 1018、Springer-Verlag、248–256 ページ、文書: 10.1007/BFb0071635 ^ ハルドーソン、M.; キタエフ、S. ピャトキン、A. （2016)。「半推移的な方向性と単語で表現可能なグラフ」。ディスクリプション応用数学。201 : 164–171. 土井：10.1016/j.dam.2015.07.033。S2CID 26796091。
^ チェン、TZQ; キタエフ、S. 日曜日、BY （2016)。「三角格子グラフの面分割の単語表現性」。グラフと結合。32 (5): 1749 ～ 1761 年。arXiv : 1503.08002。土井：10.1007/s00373-016-1693-z。S2CID 43817300。
^ チェン、TZQ; キタエフ、S. 日曜日、BY （2016)。「格子で覆われた円柱グラフの三角形分割の単語表現性」。ディスクリプション応用数学。213 : 60-70。arXiv : 1507.06749。土井：10.1016/j.dam.2016.05.025。S2CID 26987743。
^ ヒメネス、オメル; ノイ、マーク（2009)。「平面グラフの漸近列挙と極限法則」。アメリカ数学協会の雑誌。22 (2): 309–329。arXiv : math/0501269。Bibcode : 2009JAMS…22..309G。土井：10.1090/s0894-0347-08-00624-3。S2CID 3353537。
^ コリン・マクダーミッド; アンジェリカ・シュテーガー; ウェールズ人、ドミニク JA （2005)。「ランダム平面グラフ」。組み合わせ理論ジャーナル、シリーズ B。93 (2): 187–205。CiteSeerX 10.1.1.572.857。土井：10.1016/j.jctb.2004.09.007。
^ ボニション、N.; ガボイル、C. ハヌッセ、N. ポラロン、D. シェーファー、G. （2006)。「整然としたマップとツリーによる平面グラフ」。グラフと組み合わせ論。22 (2): 185–202。CiteSeerX 10.1.1.106.7456。土井：10.1007/s00373-006-0647-2。S2CID 22639942。

^ ドゥイモヴィッチ、ヴィダ; ジョレット、グウェナエル。ミチェク、ピョートル。パット・モーリン; ウエケルト、トルステン。Wood、David R. （2020)、「平面グラフにはキュー番号が制限されている」、Journal of the ACM、67 (4): 22:1–22:38、arXiv : 1904.04791、doi : 10.1145/3385731
^ ボーズ、プロセンジット; Dujmović，ヴィダ; ジャヴァルシネ、メエルヌーシュ。モーリン、パット（2020)、平面グラフの漸近的に最適な頂点ランキング、arXiv : 2007.06455
^ デンブスキ、ミハウ; フェルスナー、ステファン。ミチェク、ピョートル。Schröder、Felix （2021)、「Enhanced Bounds for Centered Colorings」、Advances in Combinatorics、arXiv : 1907.04586、doi : 10.19086/aic.27351、S2CID 195874032
^ フィロッティ、IS; メイヤー、ジャック N. (1980)。「固定種数のグラフの同型性を決定するための多項式時間アルゴリズム」。コンピューティング理論に関する第 12 回年次 ACM シンポジウムの議事録(PDF)。236–243ページ。土井: 10.1145/800141.804671。ISBN 978-0-89791-017-0。S2CID 16345164。

参考文献
Kuratowski、Kazimierz (1930)、「Sur le problème des courbes gauches en topologie」 (PDF)、Fundamenta Mathematicae (フランス語)、15 : 271–283、doi : 10.4064/fm-15-1-271-283。
Wagner， K. (1937)、「Über eine Eigenschaft der ebenen Komplexe」、Mathematische Annalen (ドイツ語)、114 : 570–590、doi : 10.1007/BF01594196、S2CID 123534907。
ボイヤー、ジョン・M. Myrvold， Wendy J. （2005)、「最先端: エッジ追加による単純化された O(n) 平面性」 (PDF)、Journal of Graph Algorithms and Applications、8 (3): 241–273、doi : 10.7155/jgaa .00091。
ブレンダン・マッケイ; Brinkmann、Gunnar、便利な平面グラフジェネレーター。
de Fraysseix、H. オッソナ・デ・メンデス、P. ; Rosenstiehl， P. （2006)、「Trémauxtrees and planarity」、International Journal of Foundations of Computer Science、17 (5): 1017–1029、arXiv : math/0610935、doi : 10.1142/S0129054106004248、S2CID 40107560。グラフ描画特集。
バーダー， DA ; スレシュタ、S. （2003 年 10 月 1 日)。平面性検査のための新しい並列アルゴリズム(技術レポート)。UNM-ECE テクニカルレポート 03-002。2016年3月16日のオリジナルからアーカイブ。
フィスク、スティーブ (1978)、「Chvátal のウォッチマン定理の短い証明」、Journal of Combinatorial Theory、シリーズ B、24 (3): 374、doi : 10.1016/0095-8956(78)90059-X。

外部リンク

コモンズには、平面グラフ
に関連するメディアが
Edge Addition Planarity Algorithm Source Code、バージョン 1.0 — Boyer-Myrvold 平面性アルゴリズムのリファレンス実装用の無料 C ソースコード。組み合わせ平面エンベッダーと Kuratowski サブグラフアイソレーターの両方を提供します。無料ライセンスのオープンソースプロジェクトでは、Edge Addition Planarity Algorithms (現在のバージョン)が提供されます。
グラフアルゴリズムライブラリとエディタの公開実装— 平面性テスト、平面性エンベッダー、および線形時間での Kuratowski サブグラフ表示を含む GPL グラフアルゴリズムライブラリ。
平面グラフ用のブーストグラフライブラリツール(線形時間平面性テスト、埋め込み、Kuratowski サブグラフ分離、直線描画など)。
3 つのユーティリティパズルと平面グラフ
NetLogo Planarity モデル— John Tantalo のゲームの NetLogo バージョン”