プランク定数

Planck_constant

黒体放射を支配する法則については、「プランクの法則」を参照して
プランク定数、またはプランク定数 は、量子力学において基本的に重要な基本的な物理定数です。この定数は、光子のエネルギーとその周波数の関係を示し、質量エネルギー等価性によって質量と周波数の関係を示します。具体的には、光子のエネルギーは、その周波数にプランク定数を乗じたものに等しくなります。定数は一般に次のように表されます。 h {textstyle h}
。換算プランク定数、またはディラック定数、定数を で割ったものに等しい2 π
{textstyle 2pi }
、で表されます ℏ {textstyle hbar }プランク定数
一般的な記号 h { h}
、 また ℏ { hbar }
減少したプランク定数の場合
寸法 2 − 1
{ {mathsf {M}}{mathsf {L}}^{2}{mathsf {T}}^{-1}}
計測学では、他の定数とともに、SI質量単位であるキログラムを定義するために使用されます。 SI 単位は、プランク定数を SI 単位で表現したときに正確な値が得られるように定義されています。 h { h}=6.626 070 15 × 10 −34  J⋅Hz −1。
この定数は、紫外線災害に対する解決策の一環として、1900 年にマックス プランクによって初めて仮定されました。19 世紀末には、黒体放射のスペクトルの正確な測定値が存在していましたが、より高い周波数でのそれらの測定値の分布は、当時存在していた理論によって予測されたものとは大きく異なりました。プランクは、観測されたスペクトルの式を経験的に導き出しました。彼は、黒体放射を含む空洞内の仮想の帯電発振器は、量子化されたステップでのみそのエネルギーを変化させることができ、それらのステップのエネルギーは発振器に関連する電磁波の周波数に比例すると仮定しました。彼は実験測定から比例定数を計算することができ、その定数は彼にちなんで名付けられました。
1905 年、アルバート アインシュタインは、電磁波自体のエネルギーの「量子」または最小要素を決定しました。光量子はある面では電気的に中性の粒子として振る舞い、最終的には光子 と呼ばれるようになりました。マックス・プランクは、「エネルギー量子の発見により物理学の進歩に貢献した功績が認められて」 1918年のノーベル物理学賞を受賞した。
価値観
絶え間ない
SI単位
eVの単位
h 6.626 070 15 × 10 −34  J⋅Hz −1
4.135 667 696 … × 10 −15  eV⋅Hz −1
ħ 1.054 571 817 … × 10 −34  J⋅
6.582 119 569 … × 10 −16  eV・s
HC 1.986 445 86 … × 10 −25  J · m 1.239 841 98 …  eV ⋅ μm
ジェク 3.161 526 77 … × 10 −26  J ⋅ m 0.197 326 9804 …  eV ⋅ μm

コンテンツ
1 定数の由来
2 開発と応用
2.1 光電効果 2.2 原子構造 2.3 不確定性原理
3 光子エネルギー
3.1 ド・ブロイ波長 3.2 統計力学
4 減少したプランク定数
5 価値
5.1 hの値の「固定」について理解する 5.2 値の重要性
6 決定
6.1 ジョセフソン定数 6.2 キブルのバランス 6.3 磁気共鳴 6.4 ファラデー定数 6.5 X線結晶密度 6.6 粒子加速器
7 こちらも参照
8 ノート
9 参考文献
9.1 引用 9.2 情報源
10 外部リンク

定数の由来
詳細は「プランクの法則」を参照

ベルリンのフンボルト大学の銘板: 「作用の初等量子hを発見したマックス プランクは、1889 年から 1928 年までここで教えました。」

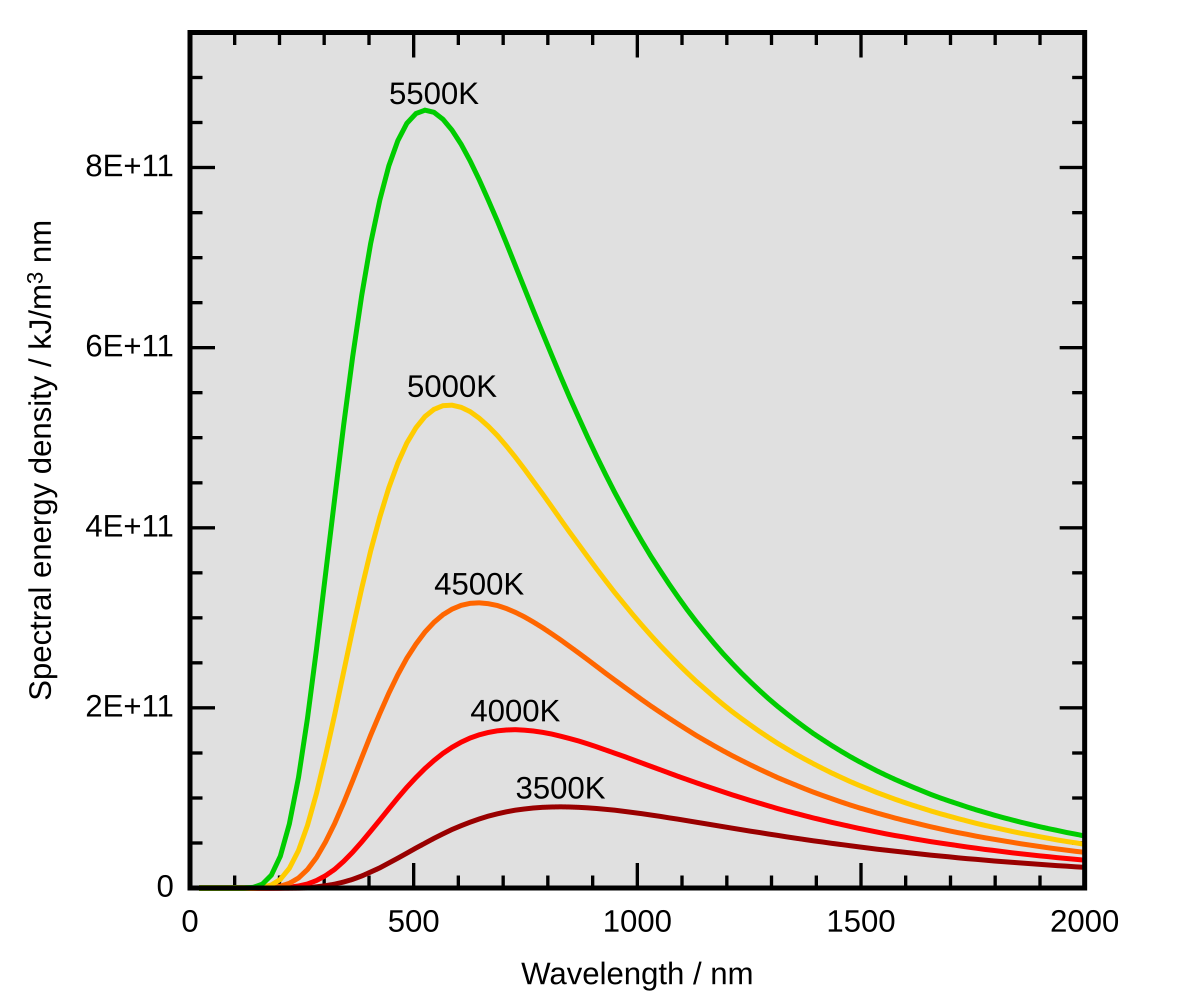
黒体から発せられる光の強度。各曲線は、さまざまな体温での動作を表します。プランク定数h は、こ​​れらの曲線の形状を説明するために使用されます。
プランク定数は、密閉炉から観測された熱放射 (黒体放射) のスペクトル分布を正確に予測する数式を作成するというマックス プランクの成功した取り組みの一環として定式化されました。この数式は現在プランクの法則として知られています。
19 世紀の最後の数年間、マックス プランクは、約 40 年前にキルヒホッフによって最初に提起された黒体放射の問題を調査していました。すべての肉体は、自発的かつ継続的に電磁放射線を放出します。観察された発光スペクトルの全体的な形状についての表現や説明はありませんでした。当時、ウィーンの法則は短波長と高温のデータには適合していましたが、長波長では当てはまりませんでした。 : 141 またこの頃、プランクには知られていなかったが、レイリー卿は、現在ではレイリー・ジーンズの法則として知られる公式を理論的に導出しており、この公式は長い波長を合理的に予測できたが、短い波長では劇的に失敗した。
この問題にアプローチして、プランクは、光の運動方程式は、考えられる周波数ごとに 1 つずつ、一連​​の調和振動子を記述すると仮説を立てました。彼は、ウィーンの法則と一致させようとして、振動子のエントロピーが身体の温度によってどのように変化するかを調べ、黒体スペクトルの近似的な数学関数を導き出すことができました 。これにより、長波長に対する簡単な経験式が得られます。 。
プランクは、ウィーンの法則（短波長の場合）と経験式（長波長の場合）を再現できる数式を見つけようとしました。この式には定数が含まれていました。 h { h}

、これは Hilfsgrosse (補助変数) のためのものと考えられており、その後プランク定数として知られるようになりました。プランクによって定式化された式は、絶対温度Tにおける周波数 νに対する物体の分光放射輝度は次の式で与えられることを示しました。
B ν ( ν T) = 2 h
ν3 2 1e h ν k B T − 1 { B_{nu }(nu ，T)={frac {2hnu ^{3}}{c^{2}}}{frac {1}{e^{frac {h nu }{k_{mathrm {B} }T}}-1}}，}

どこk B
{ k_{text{B}}}

はボルツマン定数、 h { h}

はプランク定数であり、 c { c}

物質であれ真空であれ、媒質中の光の速度です。
物体の分光放射、B ν
{ B_{nu }}

、さまざまな放射周波数で放出されるエネルギーの量を表します。これは、体の単位面積あたり、放射の単位立体角あたり、単位周波数あたりに放射されるパワーです。分光放射輝度は単位波長ごとに表現することもできます λ { lambda }

単位周波数ごとではなく。この場合、それは次のように与えられます。B λ( λ T) = 2 h
c2 5 1e h c λ k B T − 1 { B_{lambda }(lambda ，T)={frac {2hc^{2}}{lambda ^{5}}}{frac {1}{e^{frac {hc}{ lambda k_{mathrm {B} }T}}-1}}，}

これは、より短い波長で放出される放射エネルギーが、より長い波長で放出されるエネルギーよりも温度とともにどのように急速に増加するかを示しています。
プランクの法則は、特定の波長で放出される光子の数や放射線量内のエネルギー密度など、他の用語で表現されることもSI単位_B ν
{ B_{nu }}

はW · sr −1 · m −2 · Hz −1ですが、B λ
{ B_{lambda }}

はW・sr -1・m -3です。
プランクはすぐに、自分の解決策がユニークではないことに気づきました。いくつかの異なる解決策があり、それぞれが発振器のエントロピーに異なる値を与えました。プランクは自分の理論を守るために、当時物議を醸していた統計力学の理論を使用することにしましたが、これを「絶望的な行為でした…私は物理学についてのこれまでの信念をすべて犠牲にする用意ができていました。」彼の新しい境界条件の 1 つは、
U N を、無限に割り切れる連続量としてではなく、整数の有限等分で構成される離散量として解釈します。このような各部分をエネルギー要素 ε と呼びましょう。— プランク、通常スペクトルにおけるエネルギー分布の法則について
この新しい条件により、プランクは振動子のエネルギーの量子化を課しました。これは彼自身の言葉によれば「純粋に形式的な仮定でした…実際にはそれについてはあまり考えていませんでした…」が、物理学に革命をもたらすものでした。この新しいアプローチをウィーンの変位則に適用すると、「エネルギー要素」が振動子の周波数に比例する必要があることが示されました。これは、現在「プランク – アインシュタインの関係」と呼ばれることがあるものの最初のバージョンです。E = h
f { E=hf.}

プランクは次の値を計算することができました。 h { h}

黒体放射に関する実験データから: 彼の結果、6.55 × 10 -34  J⋅s は、現在定義されている値の 1.2% 以内です。彼はまた、ボルツマン定数の最初の決定も行いました。k B
{ k_{text{B}}}

同じデータと理論に基づいています。

さまざまな温度で観察されたプランク曲線、および 5000K で観察されたプランク曲線からの理論上のレイリー ジーンズ (黒) 曲線の発散。

開発と応用
黒体問題は 1905 年に再検討され、レイリー卿とジェームス ジーンズ(一方で)、そしてアルバート アインシュタイン(他方) が、古典的な電磁気学では観測されたスペクトルを決して説明できないことを個別に証明しました。これらの証明は、1911 年にパウル・エーレンフェストによって造られた名前である「紫外線カタストロフ」として一般に知られています。これらの証明は、プランクの量子化エネルギー準位の公準が単なる数学的なものではないことを物理学者に納得させるのに（アインシュタインの光電効果に関する研究と合わせて）大きく貢献しました。形式主義。1911 年の最初のソルベイ会議では、「放射線と量子の理論」が取り上げられました。

光電効果
詳細は「光電効果」を参照
光電効果は、光が当たると表面から電子 (「光電子」と呼ばれる) が放出されることです。この現象は1839 年にアレクサンドル・エドモン・ベクレルによって初めて観察されましたが、通常は 1887 年に最初の徹底的な調査を発表したハインリヒ・ヘルツ の功績が認められています。別の特に徹底的な調査は、1902 年にフィリップ・レナール (レナード・フューロップ) によって発表されました。]光量子の観点から効果を論じたアインシュタインの 1905 年の論文は、彼の予測がロバート・アンドリュース・ミリカンの実験研究によって確認された後、 1921 年にノーベル賞を受賞することになりました。ノーベル委員会は、相対性理論ではなく光電効果に関する彼の研究に賞を与えたが、その理由は、発見や実験に基づいていない純粋に理論物理学に対する偏見と、実際の証明に関して委員の間で反対意見があったためである。相対性理論は実在したのです。
アインシュタインの論文が発表される前は、可視光などの電磁放射線は波として振る舞うと考えられていたため、さまざまな種類の放射線を特徴付けるために「周波数」と「波長」という用語が使用されていました。一定時間内に波によって伝達されるエネルギーは、その強度と呼ばれます。劇場のスポットライトからの光は家庭用の電球からの光よりも強いです。つまり、たとえ光の色が非常に似ていても、スポットライトは通常の電球よりも単位時間および単位空間あたりより多くのエネルギーを放出します (したがって、より多くの電力を消費します)。音や海岸に打ち寄せる波など、他の波にも強度がしかし、光電効果のエネルギー説明は、光の波動記述と一致していないようでした。
光電効果の結果として放出される「光電子」は、測定可能な特定の運動エネルギーを持っています。この運動エネルギー (各光電子の) は光の強度には依存しませんが、周波数には線形に依存します。周波数が低すぎる場合 (材料の仕事関数より小さい光子エネルギーに相当)、エネルギーの合計が のエネルギーよりも大きい複数の光子がない限り、光電子はまったく放出されません。光電子は実質的に同時に作用します (多光子効果)。周波数が光電効果を引き起こすのに十分に高いと仮定すると、光源の強度が増加すると、より高い運動エネルギーで同じ数の光電子が放出されるのではなく、同じ運動エネルギーでより多くの光電子が放出されます。
これらの観察に対するアインシュタインの説明は、光自体が量子化されているというものでした。光のエネルギーは古典的な波のように連続的に伝達されるのではなく、小さな「パケット」または量子としてのみ伝達されるということです。後に光子と名付けられるこれらのエネルギーの「パケット」のサイズは、プランクの「エネルギー要素」と同じになるはずで、プランクとアインシュタインの関係の現代版が得られます。E = h
f { E=hf.}

アインシュタインの仮説は後に実験的に証明されました: 入射光の周波数間の比例定数 f { f}

そして光電子の運動エネルギー E { E}

プランク定数と等しいことが示されました h { h}

。

原子構造
詳細は「ボーア模型」を参照

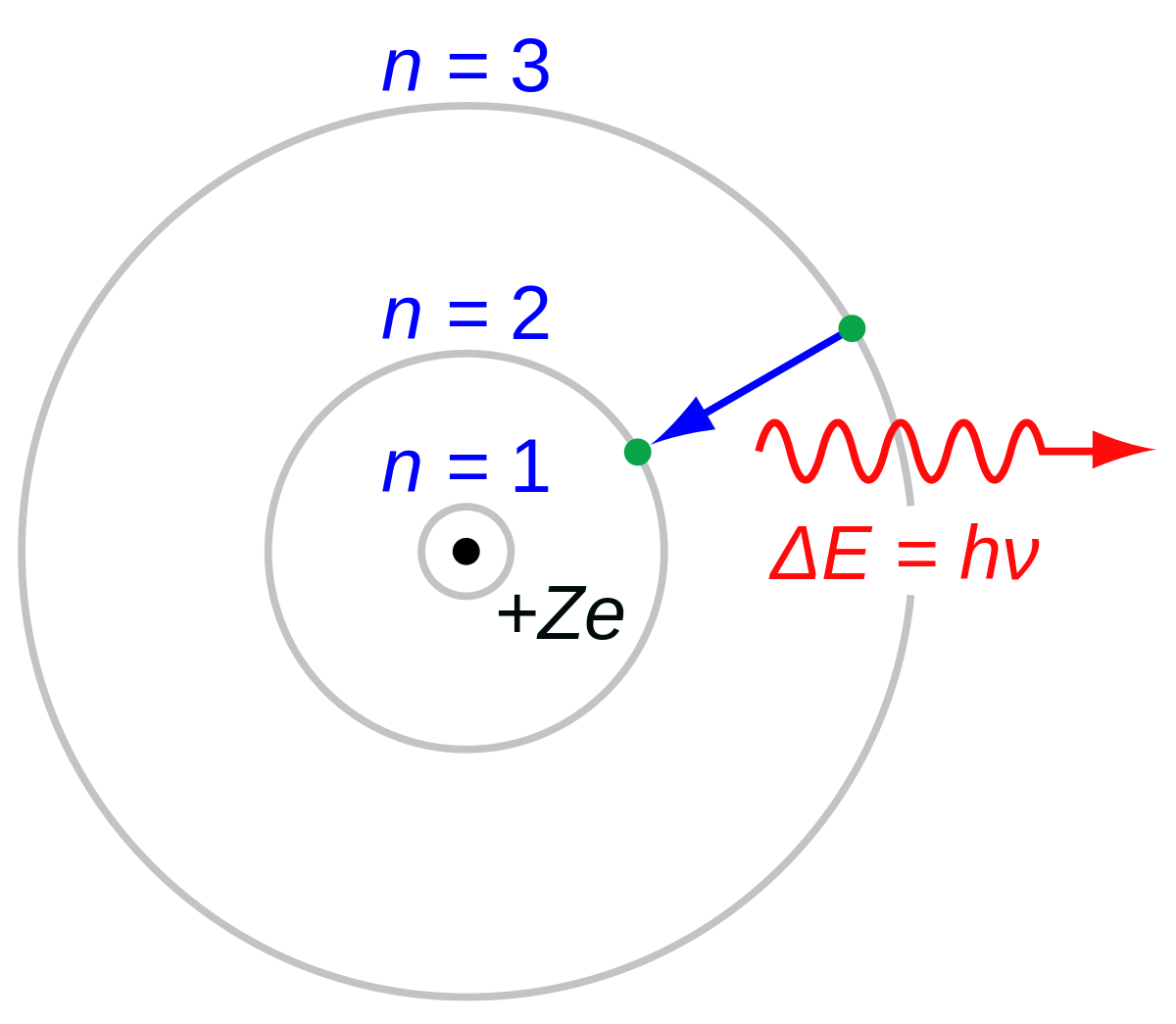
水素原子のボーア模型の図式化。モデルが予測するように、
n = 3レベルからn = 2レベルへの遷移により、波長 656 nm (赤色) の可視光が生じます。
1912 年に h-bar を原子理論に導入したのはジョン ウィリアム ニコルソンでした。h -bar は最初の量子および核原子であり、角運動量をh /2 πとして初めて量子化しました。 ニールス・ボーアは、原子のボーアモデルに関する 1913 年の論文で彼の言葉を引用した。ボーアのモデルに対するニコルソンの核量子原子モデルの研究の影響については、多くの歴史家によって書かれています。
ニールス・ボーアは、ラザフォードの古典的モデルの大きな欠点を克服するために、1913 年に原子の 3 番目の量子化モデルを導入しました。原子の最初の量子化モデルは 1910 年にArthur Erich Haasによって導入され、1911 年のソルベイ会議で議論されました。 古典的な電気力学では、円の中を移動する電荷は電磁放射を放射するはずです。その電荷が原子核の周りを回る電子である場合、放射線によって電子はエネルギーを失い、らせん状に原子核内に落ちていきます。ボーアは、プランクの研究を明確に参照してこのパラドックスを解決しました。ボーア原子内の電子は、特定の定義されたエネルギーのみを持つことができます。E n
{ E_{n}}
E n = − h c R ∞ n 2 { E_{n}=-{frac {hcR_{infty }}{n^{2}}}，}

どこ c { c}

は真空中での光の速度、R ∞
{ R_{infty }}

は実験的に決定された定数 (リュードベリ定数) であり、n ∈ {
1 2 3
、 。 }
{ nin {1，2，3，…}}

。電子が最低のエネルギー準位に達すると ( n= 1
{ n=1}

）、原子核（エネルギーが低い）にこれ以上近づくことはできません。このアプローチにより、ボーアは、水素の原子スペクトルの経験的記述であるリュードベリの公式を説明し、リュードベリ定数の値を説明することもできました。R ∞
{ R_{infty }}

他の基本定数に関しては。
ボーアは量も導入しましたℏ = h 2 π
{ hbar ={frac {h}{2pi }}}

は現在、角運動量の量子として換算プランク定数またはディラック定数として知られています。当初、ボーアはこれが原子内の各電子の角運動量であると考えましたが、これは誤りであることが判明し、ゾンマーフェルトらの開発にもかかわらず、電子の角運動量の正確な記述はボーア模型を超えていることが証明されました。電子の正しい量子化規則（水素原子の場合、エネルギーはボーアモデル方程式に還元されます）は、1925 年にハイゼンベルクの行列力学と 1926 年にシュレディンガー波動方程式によって与えられました。還元されたプランク定数は依然として基本量子です。角運動量。現代風に言えば、 J { J}

は回転不変性を持つシステムの合計角運動量であり、J z
{ J_{z}}

任意の方向に沿って測定された角運動量、これらの量は次の値のみを取ることができます。J 2 = j( j+ 1 ) ℏ 2 j = 0 1
2 1 3
2 …Jz =
メートル
ℏ メートル= −
j −j +
1 … j { {begin{aligned}J^{2}=j(j+1)hbar ^{2}，qquad &j=0，{tfrac {1}{2}}，1，{tfrac {3}{2}}，ldots ，\J_{z}=mhbar ，qquad qquad quad &m=-j，-j+1，ldots ，j.end{aligned}}}

不確定性原理
詳細は「不確定性原理」を参照
プランク定数は、ヴェルナー ハイゼンベルクの不確定性原理の記述にも現れます。同じ状態で準備された多数の粒子、その位置の不確実性を考慮すると、 ΔX { デルタ x}

、そしてその勢いの不確実性、Δ pX
{ Delta p_{x}}

、 従うΔX Δ pX ≥ ℏ
2 { Delta x，Delta p_{x}geq {frac {hbar }{2}}，}

ここで、不確実性は、期待値からの測定値の標準偏差として与えられます。同様の規則に従う、物理的に測定可能な共役変数のこのようなペアが他にもいくつか一例としては、時間とエネルギーの関係です。2 つの共役変数の不確実性間の逆関係により、一方の量をより正確に測定するともう一方の量が不正確になるため、量子実験ではトレードオフが生じます。
量子力学的定式化における特定の値の解釈の基礎となるいくつかの仮定に加えて、理論全体の基本的な基礎の 1 つは位置演算子間の交換子関係にX
^ { {hat {x}}}

そして運動量演算子 p ^ { {hat {p}}}
: [ p
^ I X j 】 = − I ℏ δ I
j { [{hat {p}}_{i}，{hat {x}}_{j}]=-ihbar delta _{ij}，}