Treap
でコンピュータサイエンス、treapおよび無作為化二分探索木は二分探索木の密接に関連する2つの形態であるデータ構造命じたキーの動的なセットを維持し、許可のバイナリ検索をキーの間で。キーの挿入と削除のシーケンスの後、ツリーの形状は、ランダムな二分木と同じ確率分布を持つ確率変数になります。特に、その高さはキーの数の対数に比例する可能性が高いため、検索、挿入、または削除の各操作の実行には対数時間がかかります。 Treap タイプ
ランダム化された二分探索木
時間複雑で大きなO記法
アルゴリズム
平均
最悪の場合
スペース
O(n)
O(n)
検索
O(log n)
O(n)
入れる
O(log n)
O(n)
消去
O(log n)
O(n)
コンテンツ
1 説明
2 オペレーション
2.1 基本操作 2.2 Treapを構築する 2.3 一括操作
3 ランダム化された二分探索木
3.1 比較
4 暗黙のtreap
4.1 オペレーション
4.1.1 要素を挿入
4.1.2 要素を削除
4.1.3 与えられた範囲の合計、最小値、または最大値を見つけます
4.1.4 与えられた範囲での追加/ペイント
4.1.5 与えられた範囲で反転
5 も参照してください
6 参考文献
7 外部リンク
説明
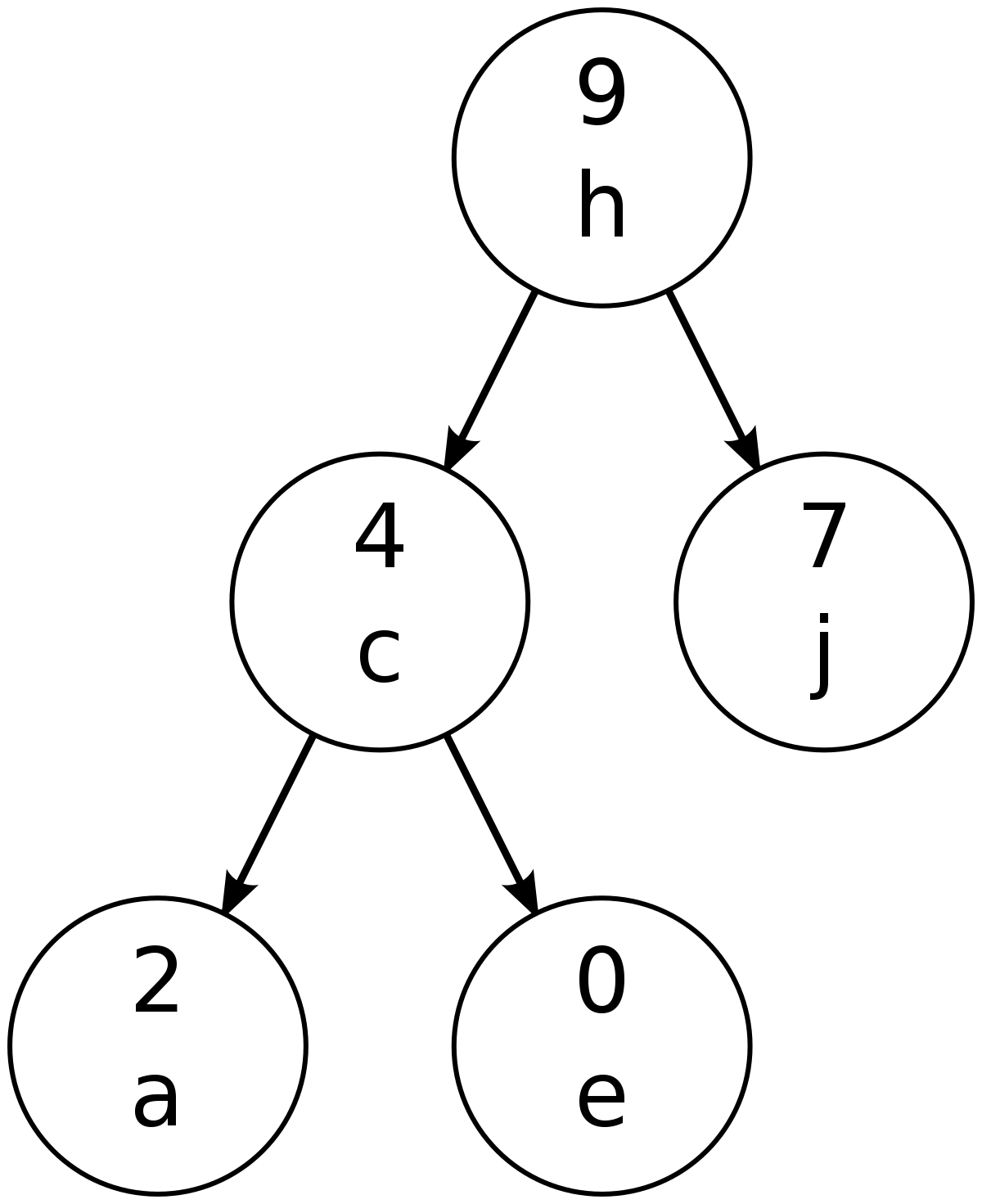
アルファベットキーと数値の最大ヒープ順序のtreap
このトレップは、1989年にライムンドザイデルとセシリアR.アラゴンによって最初に説明されました。 その名前は木と山のかばん語です。これは、各キーに(ランダムに選択された)数値の優先順位が与えられたデカルトツリーです。他の二分探索木と同様に、ノードの順序どおりの走査順序は、キーの並べ替え順序と同じです。ツリーの構造は、ヒープ順であるという要件によって決定されます。つまり、非リーフノードの優先順位番号は、その子の優先順位以上である必要がしたがって、より一般的なデカルトツリーと同様に、ルートノードは最大優先度ノードであり、その左右のサブツリーは、ソートされた順序のサブシーケンスからそのノードの左右に同じ方法で形成されます。
treapを説明する同等の方法は、リバランスを行わずに、ノードを最も優先度の高いものからバイナリ検索ツリーに挿入することによって形成できることです。したがって、優先度が独立した乱数である場合(2つのノードが同じ優先度を持つ可能性が非常に低いことを保証するために、可能な優先度の十分な大きさの空間にわたる分布から)、treapの形状はの形状と同じ確率分布を持ちます。ランダムバイナリ検索ツリー、ランダムに選択されたオーダーにリバランスすることなく、ノードを挿入することによって形成された探索木。ランダム二分探索木は対数の高さを持つ可能性が高いことが知られているため、同じことがtreapにも当てはまります。これは、クイックソートが期待どおりに実行される二分探索木の引数を反映しています O (( ログ )。
{O(n log n)}
時間。二分探索木が動的問題バージョンのソートの解決策である場合、Treapsは特に動的クイックソートに対応し、優先順位がピボットの選択を導きます。
AragonとSeidelは、頻繁にアクセスされるノードに高い優先度を割り当てることも提案しています。たとえば、アクセスごとに乱数を選択し、ノードの優先度が以前の優先度よりも高い場合はその番号に置き換えます。この変更により、ツリーはランダムな形状を失います。代わりに、頻繁にアクセスされるノードはツリーのルートの近くにある可能性が高く、ノードの検索が高速になります。
NaorとNissim は、公開鍵暗号システムで認証証明書を維持するためのアプリケーションについて説明しています。
オペレーション編集
基本操作
Treapは、次の基本的な操作をサポートします。
特定のキー値を検索するには、優先順位を無視して、バイナリ検索ツリーで標準のバイナリ検索アルゴリズムを適用します。
新しいキーを挿入するにはXをtreapに、ランダム優先発生yのためのxを。以下のためのバイナリ検索のxツリー内で、バイナリ検索はのためのノードを決定するのリーフ位置に新しいノードを作成し、xが存在している必要が次に、xがツリーのルートではなく、その親zよりも優先順位が大きい限り、xとzの間の親子関係を逆にするツリーローテーションを実行します。
ノードxをtreapから削除するには、xがツリーの葉である場合は、単にそれを削除します。場合、xは、単一の子の持つZを、削除Xツリーとメイクからzはの親の子であるX(またはメークzの場合は、ツリーの根xは親がありませんでした)。最後に、xに2つの子がある場合、ツリー内のその位置を、ソートされた順序でその直後の後続のzの位置と交換します。これにより、前のケースの1つになります。この最後のケースでは、スワップがzのヒープ順序プロパティに違反する可能性があるため、このプロパティを復元するために追加のローテーションを実行する必要がある場合が
Treapを構築する
treapを構築するには、それぞれが取るtreapにn個の値を挿入するだけです。 O (( ログ )。
{O( log n)}
時間。したがって、treapを組み込むことができます O (( ログ )。
{O(n log n)}
リスト値からの時間。
一括操作
単一要素の挿入、削除、およびルックアップ操作に加えて、いくつかの高速な「バルク」操作がtreapで定義されています:和集合、共通部分、およびセットの差。これらは、分割と結合という2つのヘルパー操作に依存しています。
これらのキーよりも小さい、2つの小さなtreapsにtreapを分割するX、及びキーより大きいもの、X挿入、X最大優先度より大きいtreap内の任意のノードの優先度よりも持つtreapに。この挿入後、xはtreapのルートノードになり、xより小さいすべての値は左側のサブトレップにあり、xより大きいすべての値は右側のサブトレップにこれは、treapへの1回の挿入と同じくらいの費用がかかります。
以前の分割の結果である2つのtreapを結合すると、最初のtreapの最大値が2番目のtreapの最小値よりも小さいと安全に想定できます。xが最初のtreapのこの最大値よりも大きく、2番目のtreapの最小値よりも小さくなるように、値xで新しいノードを作成し、最小の優先度を割り当ててから、左の子を最初のヒープに設定しますそしてその右の子は2番目のヒープになります。必要に応じて回転させて、ヒープの順序を修正します。その後、リーフノードになり、簡単に削除できます。その結果、2つの元のtreapから1つのtreapがマージされます。これは事実上分割を「元に戻す」ことであり、同じ費用がかかります。より一般的には、結合操作は、2つのtreapと任意の優先度を持つ(つまり、最高である必要はない)キーに対して機能します。
結合アルゴリズムは次のとおりです。
関数join(L、k、R) if previous(k、k(L))およびprior(k、k(R))は、 prior(k(L)、k(R)の場合はNode(L、k、R)を 返します)return Node(left(L)、k(L)、join(right(L)、k、R)) return Node(join(L、k、left(R))、k(R)、right(R) )
分割アルゴリズムは次のとおりです。
関数split(T、k) if(T = nil)return(nil、false、nil) (L、(m、c)、R)=露光(T) if(k = m)return(L、true、R) if(k
return(join(L、m、L ‘)、b、R))
2 treapsの和集合T 1及びT 2のセットを表す、A及びBはtreapのあるT表すA ∪ Bを。次の再帰的アルゴリズムは、和集合を計算します。
function union(t 1、t 2): if t 1 = nil:
return t 2 if t 2 = nil:
return t 1 if priority(t 1)
union(right(t 1)、t >))
ここで、splitは2つのツリーを返すと想定されます。1つは入力キーよりも小さいキーを保持し、もう1つは大きいキーを保持します。(アルゴリズムは非破壊的ですが、インプレース破壊的バージョンも存在します。)
交差のアルゴリズムは似ていますが、結合ヘルパールーチンが必要です。和集合、共通部分、および差のそれぞれの複雑さはO(m logNS/NS)サイズのtreapsためのMとNとM ≤ N。さらに、unionへの再帰呼び出しは互いに独立しているため、並列に実行できます。
SplitとUnionはJoinを呼び出しますが、treapのバランス基準を直接処理しません。このような実装は通常、「結合ベース」の実装と呼ばれます。
キーのハッシュ値が優先順位として使用され、構造的に等しいノードが構築時にすでにマージされている場合、マージされた各ノードはキーのセットの一意の表現になることに注意して与えられたキーのセットを表す同時ルートノードが1つしかない場合、2つのセットは、時間的に一定であるポインター比較によって等しいかどうかをテストできます。
この手法を使用すると、2つのセットの差が小さい場合にも、マージアルゴリズムを拡張して高速に実行できます。入力セットが等しい場合、和集合関数と共通部分関数はすぐに壊れて、結果として入力セットの1つを返す可能性がありますが、差分関数は空のセットを返す必要が
してみましょうdは対称差のサイズです。変更されたマージアルゴリズムもO(d log
NS/NS)。
ランダム化された二分探索木
MartínezとRouraがTreepsでのAragonとSeidelの作業に続いて導入したランダム化された二分探索木は、同じノードを同じランダムなツリー形状の分布で格納しますが、ツリーのノード内で異なる情報を順番に維持しますランダム化された構造を維持します。
ランダム化された二分探索木は、各ノードにランダムな優先順位を格納するのではなく、各ノードに小さな整数、つまりその子孫の数(それ自体を1つとして数えます)を格納します。これらの数値は、ツリーローテーション操作中に、ローテーションごとに一定の追加時間のみで維持できます。すでにn個のノードがあるツリーにキーxを挿入する場合、挿入アルゴリズムは確率1 /(n + 1)でxをツリーの新しいルートとして配置することを選択します。それ以外の場合は、挿入プロシージャを再帰的に呼び出します。左または右のサブツリー内にxを挿入します(キーがルートよりも小さいか大きいかによって異なります)。子孫の数は、各ステップでランダムに選択するために必要な確率を計算するためにアルゴリズムによって使用されます。サブツリーのルートにxを配置することは、葉に挿入してから上向きに回転させることにより、treapの場合と同様に、またはサブツリーを2つの部分に分割してサブツリーとして使用するMartínezとRouraによって記述された代替アルゴリズムによって実行できます。新しいノードの左右の子。
ランダム化された二分探索木の削除手順は、挿入手順と同じノードごとの情報を使用しますが、挿入手順とは異なり、ノードを1つのツリーに削除しました。これは、結合されるサブツリーが平均して深さΘ(logn)にあるためです。サイズnとmの2つのツリーを結合するには、平均してΘ(log(n + m))のランダムな選択が必要です。削除するノードの左または右のサブツリーが空の場合、結合操作は簡単です。それ以外の場合は、削除されたノードの左または右の子が、その子孫の数に比例する確率で新しいサブツリールートとして選択され、結合は再帰的に進行します。
比較
ランダム化されたバイナリツリーのノードごとに格納される情報は、treap(高精度の乱数ではなく小さな整数)よりも単純ですが、乱数ジェネレーターへの呼び出しの数が多くなります(O(log n)呼び出し挿入ごとに1回の呼び出しではなく、挿入または削除ごとに)、ノードごとの子孫の数を更新する必要があるため、挿入手順は少し複雑になります。技術的なわずかな違いは、treapでは、衝突の可能性が低く(2つのキーが同じ優先順位を取得する)、どちらの場合も、真の乱数ジェネレーターと疑似乱数ジェネレーターの間に統計的な違いがあることです。通常、デジタルコンピュータで使用されます。ただし、いずれの場合も、アルゴリズムの設計に使用される完全なランダム選択の理論モデルと実際の乱数ジェネレーターの機能との違いはほとんどありません。
treapとランダム化された二分探索木は両方とも更新のたびに同じランダムなツリー形状の分布を持ちますが、挿入および削除操作のシーケンスにわたってこれら2つのデータ構造によって実行されたツリーへの変更の履歴は異なる場合がたとえば、treapでは、3つの数字1、2、3が1、3、2の順序で挿入され、次に数字2が削除されると、残りの2つのノードは同じ親子関係になります。真ん中の数字を挿入する前に行いました。ランダム化された二分探索木では、削除後のツリーは、中央の番号を挿入する前のツリーの状態に関係なく、2つのノード上の2つの可能なツリーのいずれかである可能性が等しくなります。
暗黙のtreap
暗黙のtreap は、通常のtreapの単純なバリエーションであり、次の操作をサポートする動的配列と見なすことができます。 O (( ログ )。
{O( log n)}
:
任意の位置に要素を挿入する
任意の位置から要素を削除する
指定された範囲内の合計、最小、または最大要素を検索します。
追加、指定された範囲でペイント
特定の範囲の要素を反転する
暗黙のtreapの背後にある考え方は、配列要素のインデックスをtreapに格納することです。要素の実際の値は、明示的にtreapに格納されません。そうでない場合、更新(挿入/削除)により、キーが変更されます。 O (( )。
{O(n)}
ツリーのノードとこれは非常に遅いです。
ノードTのキー値(暗黙のキー)は、そのノードより少ないノードの数に1を加えたものです。TがPの右側のサブツリーにある場合、そのようなノードは、左側のサブツリーだけでなく、祖先Pの左側のサブツリーにも存在する可能性があることに注意して
したがって、ツリーを下るときにすべてのノードの合計を累積することによって操作を実行するときに、現在のノードの暗黙のキーをすばやく計算できます。この合計は、左側のサブツリーにアクセスしても変化しませんが、増加することに注意して(( L )。+ 1
{cnt(T rightarrow L)+1}
適切なサブツリーにアクセスしたとき。
暗黙的なtreapの結合アルゴリズムは次のとおりです。
void join (pitem &t 、pite l 、pite r ){
if (!l || !r )
t = l ?l :r ;
else if (l- >前> r- >前)
結合(l- > r 、l- > r 、r )、t = l ;
そうしないと
結合(r- > l 、l 、r- > l )、t = r ;
upd_cnt (t ); }
暗黙のtreapの分割アルゴリズムは次のとおりです。
void split (pitem t 、piitem &l 、pita &r 、int key 、int add = 0 ){
if (!t )
voidを返す(l = r = 0 );
int cur_key = add + cnt (t- > l ); //暗黙のキー
if (key <= cur_key )
split (t- > l 、l 、t- > l 、key 、add )、r = t ;
そうしないと
split (t- > r 、t- > r 、r 、key 、add + 1 + cnt (t- > l ))、l = t ;
upd_cnt (t ); }
オペレーション編集
要素を挿入
位置posに要素を挿入するには、split関数を呼び出して配列を2つのサブセクションとに分割し、2つのツリーを取得します。 1 {T1}
と 2 {T2}
。次にマージします 1 {T1}
結合関数を呼び出して、新しいノードを使用します。最後に、結合関数を呼び出してマージします 1 {T1}
と 2 {T2}
。
要素を削除
削除する要素を見つけて、その子LとRで結合を実行します。次に、削除する要素を、結合操作の結果であるツリーに置き換えます。
与えられた範囲の合計、最小値、または最大値を見つけます
この計算を実行するには、次の手順に従います。
最初に、そのノードによって表される範囲のターゲット関数の値を格納するための追加のフィールドFを作成します。ノードのLとRの子の値に基づいて値Fを計算する関数を作成します。ツリーを変更するすべての関数、つまり分割と結合の最後に、このターゲット関数を呼び出します。
第二に、私たちは、与えられた範囲のクエリを処理する必要があります:私たちが呼び出すのS plitの関数を2回とにtreapを分割します 1 {T1}
を含む {{ 1.。 −1 }
{ {1..A-1 }}
、 2 {T2}
を含む
{{ 。
。 }
{ {A..B }}
、 と 3 {T3} を含む
{{ +
1.。 }
{ {B + 1..n }}
。クエリに回答した後、join関数を2回呼び出して、元のtreapを復元します。
与えられた範囲での追加/ペイント
この操作を実行するには、次の手順に従います。
サブツリーの付加価値を含む追加のフィールドDを作成します。この変更をノードからその子に伝播するために使用される関数pushを作成します。ツリーを変更するすべての関数の最初にこの関数を呼び出します。つまり、ツリーに変更を加えた後、情報が失われないように、分割して結合します。
与えられた範囲で反転
特定のノードのサブツリーをノードごとに逆にする必要があることを示すために、追加のブールフィールドRを作成し、その値をtrueに設定します。この変更を伝播するために、ノードの子を交換し、それらすべてに対してRをtrueに設定します。
も参照してください
フィンガーサーチ
参考文献
^ アラゴン、セシリアR。; Seidel、Raimund(1989)、「ランダム化された探索木」 (PDF)、Proc。30番目の症状。Foundations of Computer Science(FOCS 1989)、ワシントンDC:IEEE Computer Society Press、pp。540–545、doi:10.1109 / SFCS.1989.63531、ISBN 0-8186-1982-1 ^ ザイデル、ライムンド; Aragon、Cecilia R.(1996)、「Randomized Search Trees」、Algorithmica、16(4/5):464–497、doi:10.1007 / s004539900061
^ Naor、M .; Nissim、K。、「証明書の失効と証明書の更新」(PDF)、IEEE Journal on Selected Areas in Communications、18(4):561–570、doi:10.1109 / 49.839932
。
^ Blelloch、Guy E。; Reid-Miller、Margaret(1998)、「treapsを使用した高速セット操作」、Proc。10番目のACM症状。Parallel Algorithms and Architectures(SPAA 1998)、New York、NY、USA:ACM、pp。16–26、doi:10.1145 / 277651.277660、ISBN 0-89791-989-0。
^ Liljenzin、Olle(2013)。「コンフルエントに永続的なセットとマップ」。arXiv:1301.3388。Bibcode:2013arXiv1301.3388L。
^ GitHubのコンフルエントなセットとマップ ^ マルティネス、コンラード; Roura、Salvador(1997)、「ランダム化された二分探索木」、Journal of the ACM、45(2):288–323、doi:10.1145 / 274787.274812
^ C “Treap -競争力のあるプログラミングアルゴリズム”。cp-algorithms.com 。2021-11-21を取得。
外部リンク
コモンズには、Treapに関連するメディアが
セシリア・アラゴンによるtreapリファレンスと情報のコレクション
オープンデータ構造-セクション7.2-Treap:ランダム化された二分探索木、Pat Morin
アニメーションのtreap
ランダム化された二分探索木。UIUCのジェフエリクソンによるコースからの講義ノート。タイトルにもかかわらず、これは主にtreapとスキップリストに関するものです。ランダム化された二分探索木については簡単に説明します。
JunyiSunによるtreapに基づく高性能のKey-Valueストア
treapのVB6実装。COMオブジェクトとしてのtreapのVisualBasic6実装。
TreapのActionScript3実装
純粋なPythonとCythonのメモリ内treapとduptreap
C#でのTreeps。ロイ・クレモンズ
Pure Goインメモリ、不変のtreap
PureGo永続的なtreapKey-Valueストレージライブラリ”