Types_of_mesh
メッシュは、小さい個別セルだけ大きい幾何学的ドメインの表現です。メッシュは、偏微分方程式の解を計算し、コンピューターグラフィックスをレンダリングし、地理データと地図作成データを分析するために一般的に使用されます。メッシュはスペースを要素(またはセルまたはゾーン)に分割します)方程式を解くことができます。これにより、より大きな領域で解が近似されます。要素の境界は、モデル内の内部境界または外部境界にあるように制約される場合がより高品質の(より良い形状の)要素は、より良い数値特性を持ちます。「より良い」要素を構成するものは、一般的な支配方程式とモデルインスタンスの特定の解に依存します。
コンテンツ
1 一般的なセルの形状
1.1 二次元
1.1.1 三角形
1.1.2 四辺形
1.2 三次元
1.2.1 四面体
1.2.2 ピラミッド
1.2.3 三角柱
1.2.4 六面体
1.2.5 高度なセル(多面体)
2 グリッドの分類
2.1 構造化されたグリッド 2.2 非構造格子 2.3 ハイブリッドグリッド
3 メッシュ品質
3.1 ソリューションの精度 3.2 収束率 3.3 グリッドの独立性
4 メッシュの種類を決定する
4.1 歪度
4.1.1 等辺ボリュームに基づく
4.1.2 正規化された正三角形からの偏差に基づく
4.1.3 等角スキュー
4.2 滑らかさ 4.3 アスペクト比
5 メッシュの生成と改善
6 も参照してください
7 参考文献
8 外部リンク
一般的なセルの形状編集
二次元
基本的な2次元のセル形状
一般的に使用される2次元のセル形状には2つのタイプがこれらは三角形と四辺形です。
計算上不十分な要素は、鋭い内角または短いエッジ、あるいはその両方を持ちます。
三角形
このセル形状は3つの側面で構成され、最も単純なタイプのメッシュの1つです。三角形のサーフェスメッシュは、常にすばやく簡単に作成できます。これは、非構造格子で最も一般的です。
四辺形
このセルの形状は、図に示すように基本的な4面の形状です。これは、構造化グリッドで最も一般的です。
四辺形の要素は通常、凹面になることから除外されます。
三次元
基本的な3次元セル形状
基本的な3次元要素は、四面体、四辺形ピラミッド、三角柱、および六面体です。それらはすべて三角形と四辺形の面を持っています。
押し出された2次元モデルは、完全にプリズムと六面体によって押し出された三角形と四角形として表すことができます。
一般に、3次元の四辺形の面は完全に平面ではない場合が非平面の四辺形の面は、2つの隣接する要素によって共有される薄い四面体ボリュームと見なすことができます。
四面体
四面体は4つの頂点、6辺を有し、4つの三角形の面によって制限されます。ほとんどの場合、四面体ボリュームメッシュを自動的に生成できます。
ピラミッド
四辺形ベースのピラミッドには、5つの頂点、8つのエッジがあり、4つの三角形と1つの四辺形の面で囲まれています。これらは、ハイブリッドメッシュやグリッドで、正方形と三角形の面の要素間の遷移要素として効果的に使用されます。
三角柱
三角プリズムは2三角及び3つの四辺形面で囲まれた頂点6、9つのエッジを有します。このタイプのレイヤーの利点は、境界レイヤーを効率的に解決できることです。
六面体
六面体、トポロジカル立方体は、8つの頂点、6つの四辺形面によって囲まれた12面の縁部を有しています。ヘックスまたはブリックとも呼ばれます。同じセル量の場合、六面体メッシュの解の精度が最も高くなります。
ピラミッドと三角柱のゾーンは、計算上、一部のエッジがゼロに縮小された縮退した六面体と見なすことができます。六面体の他の退化形式も表すことができます。
高度なセル(多面体)
多面体(デュアル)要素は、頂点、エッジ及び面の任意の数を有します。ネイバーの数(通常は10)のため、通常、セルごとにより多くのコンピューティング操作が必要です。これは計算の精度で補われますが。
グリッドの分類
参照:
グリッド分類
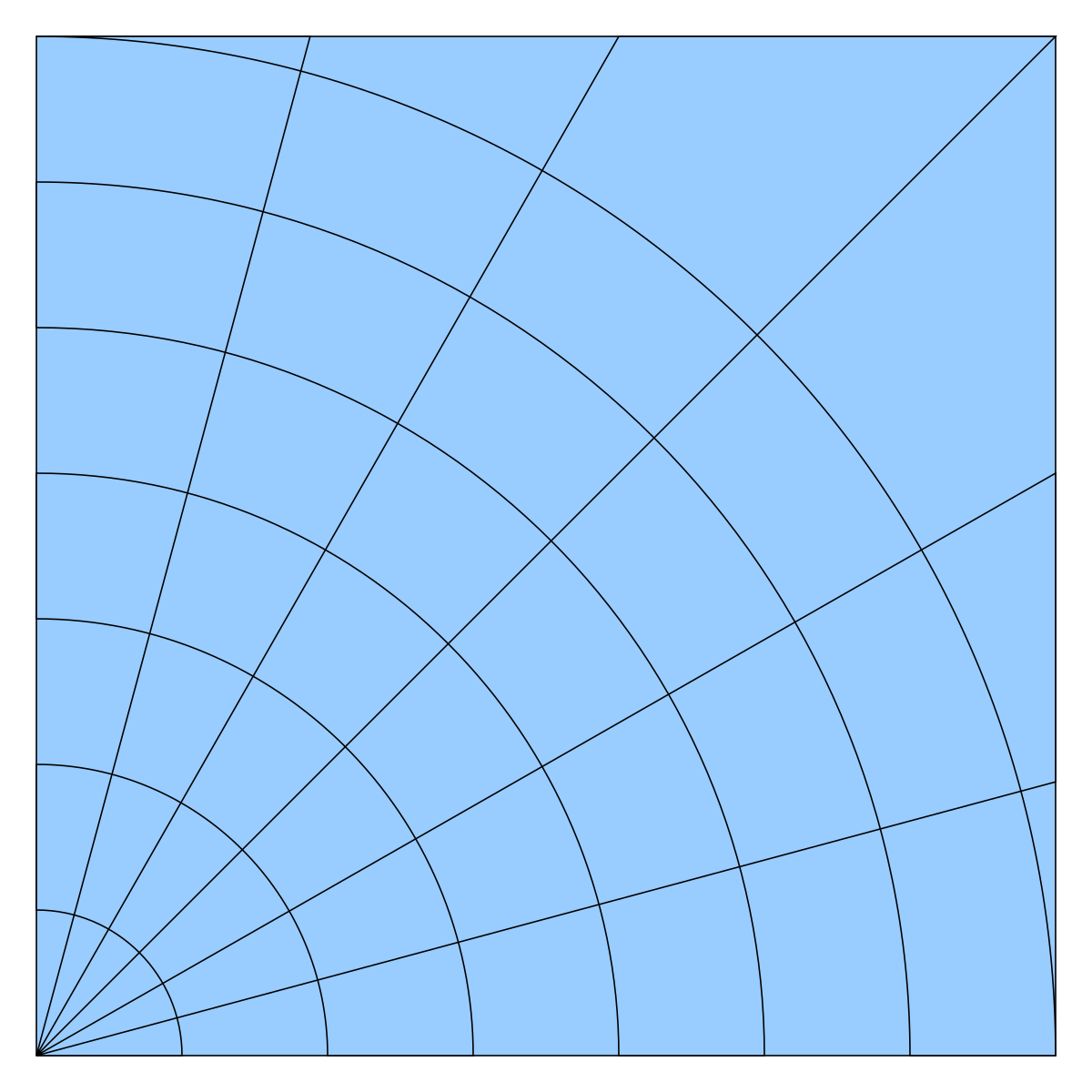
構造化グリッド

非構造格子
構造化されたグリッド
構造化グリッドは、通常の接続によって識別されます。可能な要素の選択肢は、2Dでは四辺形、3Dでは六面体です。このモデルは、近隣の関係がストレージの配置によって定義されるため、スペース効率が非常に高くなります。非構造化に対する構造化グリッドのその他の利点は、収束性と解像度が高いことです。
非構造格子
非構造格子は不規則な接続によって識別されます。コンピュータのメモリでは、2次元または3次元の配列として簡単に表現することはできません。これにより、ソルバーが使用できる可能性のある要素がすべて考慮されます。構造化メッシュと比較すると、このモデルは近隣関係の明示的な保存を必要とするため、スペース効率が非常に低くなる可能性がこれらのグリッドは通常、2Dの三角形と、3Dの四面体を使用します。
ハイブリッドグリッド
ハイブリッドグリッドには、構造化された部分と構造化されていない部分が混在しています。構造化メッシュと非構造化メッシュを効率的に統合します。ジオメトリの規則的な部分には構造化グリッドを含めることができ、複雑な部分には非構造化グリッドを含めることができます。これらのグリッドは非コンフォーマルである可能性がつまり、グリッド線はブロック境界で一致する必要はありません。
メッシュ品質
より正確な解がより迅速に計算される場合、メッシュはより高品質であると見なされます。精度と速度には緊張がメッシュサイズを小さくすると、常に精度が向上しますが、計算コストも増加します。
精度は、離散化誤差と解の誤差の両方に依存します。離散化誤差の場合、特定のメッシュは空間の離散近似であるため、方程式が正確に解かれている場合でも、近似解しか提供できません。(コンピュータグラフィックスのレイトレーシングでは、発射された光線の数が離散化エラーのもう1つの原因です。)ソリューションエラーの場合、PDEの場合、メッシュ全体で多くの反復が必要です。方程式が正確に解かれる前に、計算は早期に終了します。メッシュ要素タイプの選択は、離散化と解のエラーの両方に影響します。
精度は、要素の総数と個々の要素の形状の両方に依存します。各反復の速度は要素の数に応じて(直線的に)増加し、必要な反復の数は、ローカル要素の形状とサイズと比較したローカルソリューションの値と勾配によって異なります。
ソリューションの精度
解が一定の場合、粗いメッシュは正確な解を提供する可能性があるため、精度は特定の問題インスタンスによって異なります。解の勾配が大きい領域でメッシュを選択的に細かくすることができるため、そこでの忠実度が向上します。要素内の補間値を含む精度は、要素のタイプと形状によって異なります。
収束率
反復するたびに、計算された解と真の解の間の誤差が減少します。収束速度が速いということは、反復回数が少なく、エラーが小さいことを意味します。
品質の低いメッシュでは、流体の流れの境界層などの重要な機能が省略される場合が離散化誤差が大きくなり、収束率が低下します。解がまったく収束しない場合が
グリッドの独立性
十分な反復が与えられた場合に離散化と解の誤差が十分に小さい場合、解はグリッドに依存しないと見なされます。これは、比較結果を知るために不可欠です。メッシュ収束スタディは、要素を改良し、洗練されたソリューションを粗いソリューションと比較することで構成されます。さらに改良(またはその他の変更)してもソリューションが大幅に変更されない場合、メッシュは「独立グリッド」です。
メッシュの種類を決定する
正三角形の体積に基づく歪度
精度が最も重要な場合は、六面体メッシュが最も好ましいものです。メッシュの密度は、すべてのフローフィーチャをキャプチャするために十分に高い必要がありますが、同じように、フローの不要な詳細をキャプチャするほど高くないようにする必要がこれにより、CPUに負担がかかり、より多くの時間が無駄になります。壁が存在する場合は常に、壁に隣接するメッシュは境界層の流れを解決するのに十分なほど細かく、一般に、三角形、四面体、ピラミッドよりもクワッド、ヘックス、プリズムセルが優先されます。クワッドセルとヘックスセルは、流れが完全に発達して一次元になっている場所で伸ばすことができます。
四辺形の歪度を示します
歪度、滑らかさ、アスペクト比に基づいて、メッシュの適合性を判断できます。
歪度
グリッドの歪度は、メッシュの品質と適合性の適切な指標です。歪度が大きいと、補間された領域の精度が低下します。グリッドの歪度を決定する方法は3つ
等辺ボリュームに基づく
この方法は、三角形と四面体にのみ適用可能であり、デフォルトの方法です。
歪度 = 最適なセルサイズ-セルサイズ
最適なセルサイズ
{{ text {Skewness}} = { frac { text {最適なセルサイズ-セルサイズ}} { text {最適なセルサイズ}}}}
スムーズで大きなジャンプチェンジ
正規化された正三角形からの偏差に基づく
この方法は、すべてのセルと面の形状に適用され、ほとんどの場合、プリズムとピラミッドに使用されます。
歪度(クワッドの場合) = 最大
[ θ−90 90 90 −
θ I 90 ] {{ text {歪度(クワッドの場合)}} = max { left [{ frac { theta _ {max} -90} {90}}、{ frac {90- theta _ { min}} {90}} right]}}
等角スキュー
品質のもう1つの一般的な尺度は、等角スキューに基づいています。
等角スキュー = 最大
[ θ−
θ 180− θ
e θ
e − θ I θe ]
{{ text {Equiangle Skew}} = max { left [{ frac { theta _ {max}- theta _ {e}} {180- theta _ {e}}}、{ frac { theta _ {e}- theta _ {min}} { theta _ {e}}} right]}}
どこ:
θ{ theta _ {max} 、}




